Contoh Soal Fungsi Komposisi dan Invers dan Jawaban – Fungsi komposisi adalah susunan dari beberapa fungsi yang terhubung dan bekerjasama dapat juga diilustrasikan jika fungsi f dan g adalah mesin yang bekerja saling beriringan. Sedangkan Fungsi Invers dapat didefinisikan apabila fungsi f: A → B memiliki relasi dengan fungsi g: B → A, maka fungsi g tersebut adalah invers dari f dan dapat juga dituliskan f‾¹ atau g = f ‾¹. Jika f ‾¹ dalam bentuk fungsi, maka f ‾¹ dinyatakan fungsi invers.
Suatu fungsi atau pemetaan dapat disajikan dalam bentuk himpunan pasangan terurut, rumus, diagram panah, atau diagram cartesius. Fungsi f yang memetakan himpunan A ke himpunan B ditulis dengan notasi:
Dengan:
A disebut domain (daerah asal) dinotasikan Df
B disebut Kodomain (daerah kawan) dinotasikan
yeB | (x,y) eR, xEA disebut range (daerah hasil), dinotasikan dengan
1 – 10 Soal Fungsi Komposisi dan Invers dan Jawaban
1. Jika f (x) = px, p konstanta positif, maka
Jawaban :
2. Tentukan Fungsi :
terdefenisi untuk. . .
Jawaban :
3. Jika fungsi f di defenisikan sebagai f (x) = 2x maka nilai
Jawaban :
4. Jika f (x) = x + 3 maka f x2 + f2 (x) 2f (x) =……
Jawaban :
5. Diketahui f (x + 1) = x2 1 dan g (x) = 2x maka (g f) (x) =……
Jawaban :
Baca Juga : Soal Transformasi Geometri (Translasi, Refleksi, Rotasi, Dilatasi)
6. Jika f (x) = x3 + 2 dan g (x) = 
: x ≠ 1 maka (g o f) (x) adalah …..
Jawaban :
7. Jika f (x) =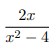 
dan g (x) = √2x maka (f o g) (x) adalah …..
Jawaban :
8. Jika f (x) = -4x dan f (g (x)) = -x/2 + 1 maka g (x) =……
Jawaban :
9.Diketahui (f o g) (x) =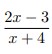 
: x ≠ -4 dan g (x) = (1 – x). Maka f (x) adalah ….
Jawaban :
10. Fungsi f : R → R dan g : R → R dinyatakan oleh f (x) = x + 2 dan (g o f) (x) = 2x2 + 4x + 1 maka g (2x) =……
Jawaban :
11 – 20 Soal Fungsi Komposisi dan Invers dan Jawaban
11. Bila f (x) = 
dengan x ≠ 3 maka invers dari f (x) adalah f‾¹ (x) = . . .
Jawaban :
12. Invers dari f (x) = (1 − x³)1/5 + 2 adalah. . .
Jawaban :
13. Jika f (x) = 3x-1 maka f‾¹ (81) = . . .
Jawaban :
14. Fungsi f : R → R dan g : R → R dirumuskan dengan f (x) = ½ x − 1 dan g (x) = 2x + 4 maka (g ◦ f)‾¹ (10) adalah …
Jawaban :
15. Jika f‾¹ (x) = 
dan g‾¹ (x) = 
maka (f ◦ g)‾¹ (6) = . . .
Jawaban :
Lihat Juga : Contoh Soal Matriks, Determinan, dan Invers
16. Jika f (x) = 
dan g (x) = x − 2 maka (g ◦ f)‾¹ (x) = . . .
Jawaban :
17. Diketahui f (x) =5log x dan g (x) = 
maka (f ◦ g)‾¹ (x) = ……
Jawaban :
18. Jika (f ◦ g) (x) = 4x² + 8x − 3 dan g (x) = 2x + 4 maka f‾¹ (x) =……
Jawaban :
19. Diketahui fungsi f dan g dinyatakan dengan f (x) = 2x + 4, g (x) =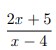 
dan h (x) = (g ◦ f‾¹)(x) dengan f‾¹ adalah fungsi invers dari f dan h‾¹ adalah invers dari h. Rumus fungsi h‾¹ (x) adalah …
Jawaban :
20. Fungsi f : R → R dan g : R → R ditentukan oleh f (x) = x + 2 dan g (x) = 2x. Jumlah akar-akar persamaan (g ◦ f) x² − 24x = 0 adalah ..
Jawaban :
Sudah selesai membaca dan berlatih soal ini ? Ayo lihat dulu Soal Matematika lainnya
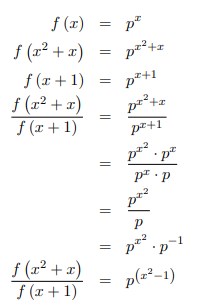
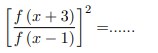
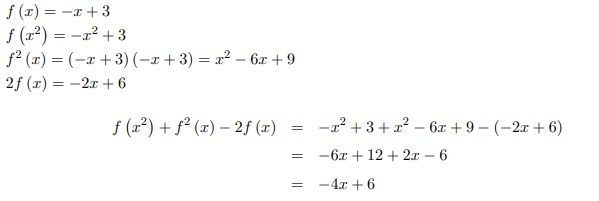
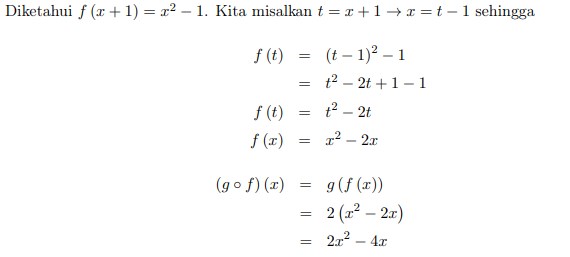
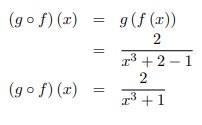
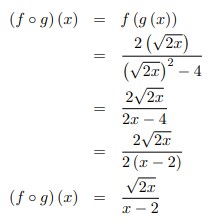
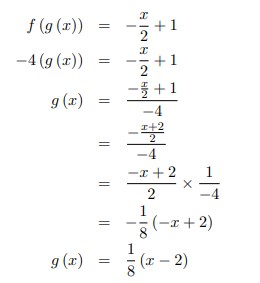
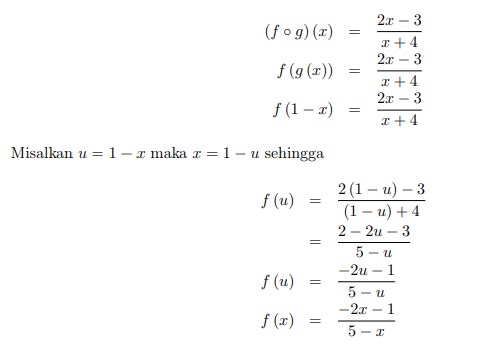
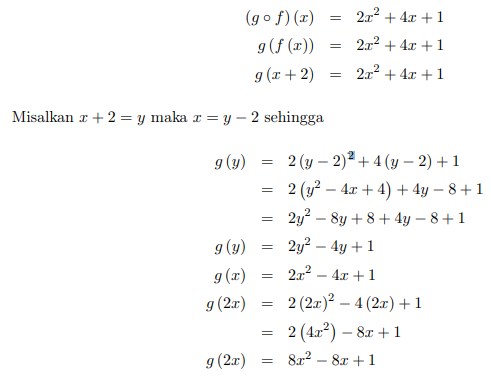
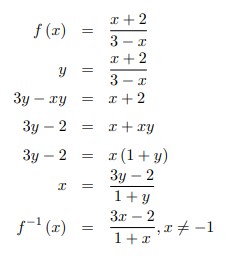
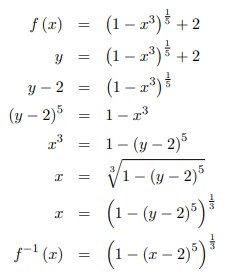
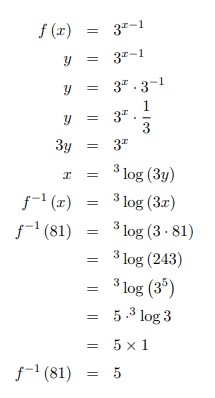
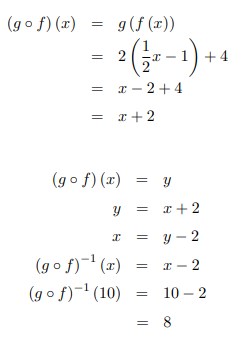
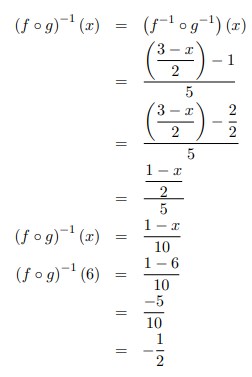
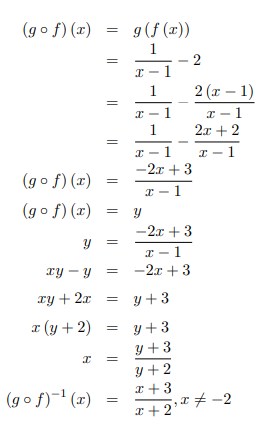
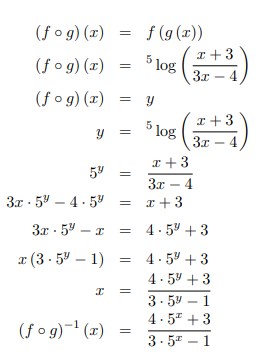
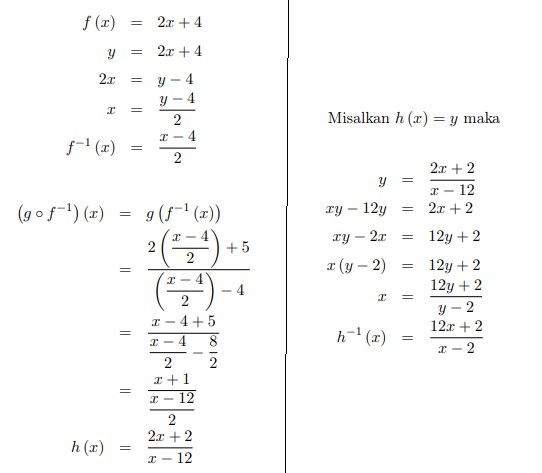
Ini sangat membantu saya
terimakasih banyak
Semoga bermanfaat 🙂
Makasiiiiqq