Contoh Soal Program Linear dan Jawaban – Program linear merupakan suatu metode penentuan nilai optimum dari suatu persoalan linear. Nilai optimum (maksimum/minimum) diperoleh dari nilai dalam suatu himpunan penyelesaian persoalan dari program linear. Persoalan linear terdapat fungsi linear yang bisa disebut sebagai fungsi objektif. Persyaratan, batasan, dan kendala dalam persoalan linear merupakan sistem pertidaksamaan linear yang akan sering keluar pada soal soal.

Grafik Pertidaksamaan Linear
Penyelesaian pertidaksamaan pada diagram cartesius, caranya sebagai berikut:
Jika garis itu tidak melalui titik (0,0) maka ambilah titik lain sebagai titik uji, yaitu (0,0)!
Jika garis itu melalui titik (0,0) maka ambilah titik lain sebagai titik uji (ambil sembarang selain titik (0,0))!
1 – 10 Soal Program Linear dan Jawaban
1. Umur pak Andi 28 tahun lebih tua dari umur Amira. Umur bu Andi 6 tahun lebih muda dari umur pak Andi. Jika jumlah umur pak Andi, bu Andi, dan Amira 119 tahun, maka jumlah umur Amira dan bu Andi adalah …. tahun
A. 86
B. 74
C. 68
D. 64
E. 58
Jawaban : C
Pembahasan :
Misalkan Umur Pak Andi=x, umur Amira=y dan umur Ibu Andi=z
x = 28 + y …(1)
z = x – 6; atau x=z+6 …(2)
x + y + z = 119 …(3)
dengan melakukan operasi penjumlahan (1) pada (2) didapatkan
2x = y + z + 34 atau 2x – y – z = 34 …(4)
Lakukan operasi penambahan (3) pada (4) atau
x + y + z = 119
2x – y – z = 34
3x =153
Atau
x = 51
Dengan melakukan substitusi x pada (1) dan (2) didapatkan
Y = 23; z = 45
Sehingga
jumlah umur Amira (y) dan bu Andi (z) adalah y + z = 23 + 45 = 68
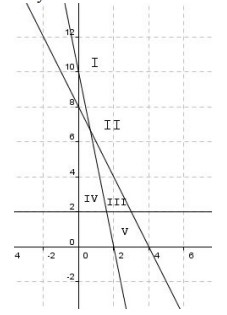
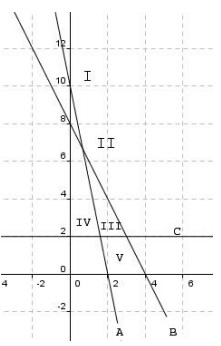
2. Himpunan penyelesaian sistem pertidaksamaan
5x + y ≥ 10
2x + y ≤ 8
y ≥ 2
ditunjukkan oleh daerah . . .
A. I
B. II
C. III
D. IV
E. V
Jawaban : C
Pembahasan :
Terlihat pada gambar bahwa A adalah persamaan garis 5x + y = 10 titik potong dengan sumbu x jika y = 0
x = 2 → titik (2,0)
titk potong dengan sumbu y jika x = 0
y = 10 → titik (0,10)
daerah 5x + y ≥ 10 berada pada garis persamaan tersebut dan di atas garis (I, II,III, V) —(a)
B adalah persamaan garis 2x + y = 8 titik potong dengan sumbu x jika y=0 x = 4 → (4,0)
titik potong dengan sumbu y jika x = 0 y = 8 → (0,8)
daerah 2x + y ≤ 8 berada pada garis persamaan tersebut dan di bawah garis (III, V) ….(b)
C adalah garis y = 2
daerah di atas garis y = 2 adalah I, II, III, IV …(b)
dari (a) , (b) dan (c) :
1) I II III V
2) III V
3) I II III IV
Yang memenuhi ketiga-tiganya adalah daerah III
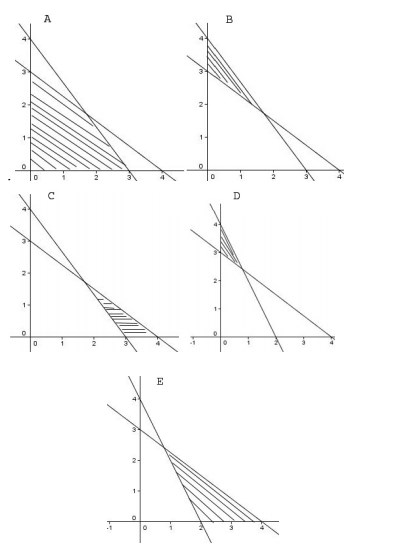
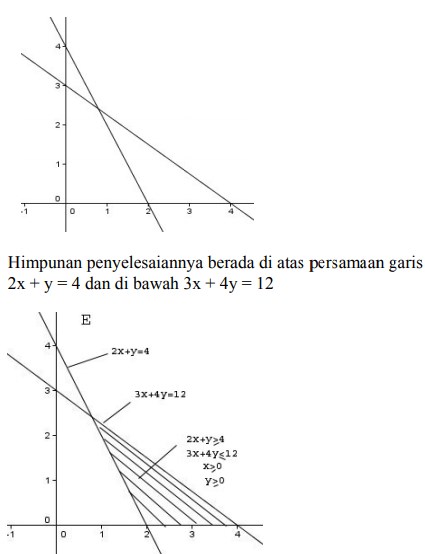
3. Himpunan penyelesaian pertidaksamaan- pertidaksamaan 2x+y≥ 4 ; 3x + 4y ≤ 12, x ≥ 0, y ≥ 0 dapat digambarkan dengan bagian bidang yang diarsir sebagai berikut :
Jawaban : E
Pembahasan :
2x + y ≥ 4 ;
2x + y = 4
titik potong dengan sumbu x , y = 0
x = 2 → (2,0)
titik potong dengan sumbu y, x = 0
y = 4 → (0,4)
3x + 4y ≤ 12
3x + 4y = 12
titik potong dengan sumbu x, y = 0
x = 4 → (4,0)
titik potong dengan sumbu y, x = 0
y=3 → (0,3)
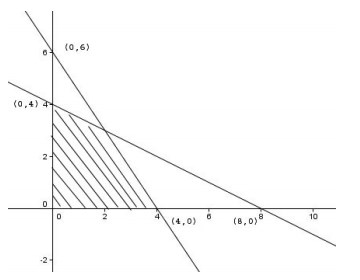
4. Daerah yang diarsir merupakan himpunan penyelesaian dari sistem pertidaksamaan linear…
A. x + 2y ≤ 8, 3x + 2y ≤ 12, x ≥ 0, y ≥ 0
B. x + 2y ≥ 8, 3x + 2y ≥ 12, x ≥ 0, y ≥ 0
C. x – 2y ≥ 8, 3x – 2y ≤ 12, x ≥ 0, y ≥ 0
D. x + 2y ≤ 8, 3x – 2y ≥ 12, x ≥ 0, y ≥ 0
E. x + 2y ≤ 8, 3x + 2y ≥ 12, x ≥ 0, y ≥ 0
Jawaban : A
Pembahasan :
karena daerah arsiran dibawah persamaan garis maka
x + 2y ≤ 8 ….(2)
Arsiran di atas sumbu x dan di kanan sumbu y maka x ≥ 0 dan y≥ 0 ….(3) dan (4)
sehingga daerah penyelesaiannya adalah:
(1), (2), (3) dan (4)
3x + 2y ≤ 12, x + 2y ≤ 8 dan x≥ 0, y≥ 0
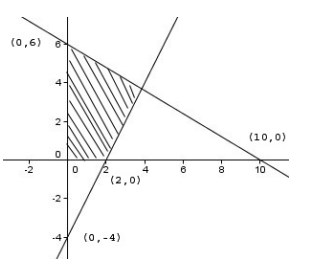
5. Daerah yang diarsir pada gambar di bawah adalah himpunan penyelesaian dari sistem pertidaksamaan…
A. 5x + 3y ≤ 30, x – 2y ≥ 4, x ≥ 0, y ≥ 0
B. 5x + 3y ≤ 30, x – 2y ≤ 4, x ≥ 0, y ≥ 0
C. 3x + 5y ≤ 30, 2x – y ≥ 4, x ≥ 0, y ≥ 0
D. 3x + 5y ≤ 30, 2x – y ≤ 4, x ≥ 0, y ≥ 0
E. 3x + 5y ≥ 30, 2x – y ≤ 4, x ≥ 0, y ≥ 0
Jawaban : D
Pembahasan :
Baca Juga Soal Pythagoras
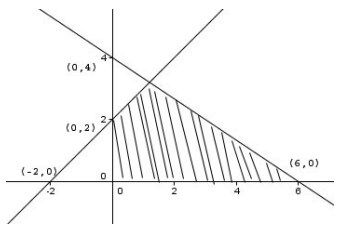
6. Daerah yang diarsir pda gambar di bawah ini menunjukkan himpunan titik (x,y) yang memenuhi pembatasan di bawah ini, yaitu ….
A. x ≥ 0, y ≥ 0, 2x + 3y ≤ 12, – x + y ≥ 2
B. x ≥ 0, y ≥ 0, 2x + 3y ≥ 12, -x + y ≥ 2
C. x ≥ 0, y ≥ 0, 2x + 3y ≤ 12, -x + y ≤ 2
D. x ≥ 0, y ≥ 0, 2x + 3y ≥ 12, -x + y ≤ 2
E. x ≥ 0, y ≥ 0, 2x + 3y ≤ 12, -x + y ≤ 2
Jawaban : C
Pembahasan :
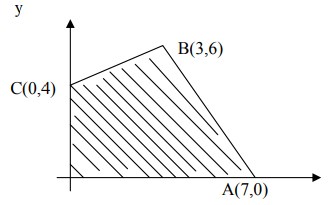
7. Daerah yang diarsir pada gambar merupakan grafik himpunan penyelesaian sistem pertidaksamaan…
A. 3x + 2y≤ 21, -2x +3y≤ 12, x≥ 0, y≥ 0
B. 2x + 3y ≤ 21, -2x – 3y ≤ 12, x ≥ 0, y ≥ 0
C. -3x + 2y ≥ 21, -2x+3y ≥ 12, x ≥ 0, y ≥ 0
D. -3x- 2y ≥ 21, 2x +3y ≥ 12, x ≥ 0, y ≥ 0
E. 3x – 2y ≥ 21, 2x -3y ≥ 12, x ≥ 0, y ≥ 0
Jawaban : A
Pembahasan :
8. Daerah yang diarsir merupakan himpunan penyelesaian suatu sistem pertidaksamaan linier.
Sistem pertidaksamaan linier itu adalah ……
A. y ≥ 0, 3x + y ≥ 6, 5x + y ≤ 20, x – y ≥ -2
B. y ≥ 0, 3x + y ≤ 6, 5x + y ≥ 20, x – y ≥ -2
C. y ≥ 0, x + 3y ≥ 6, x + 5y ≤ 20, x – y ≤ 2
D. y ≥ 0, x + 3y ≤ 6, x +5y ≥ 20, x – y ≥ -2
E. y ≥ 0, 3x – y ≥ 6, 5x -y ≤ 0, x – y ≥ -2
Jawaban : A
Pembahasan :
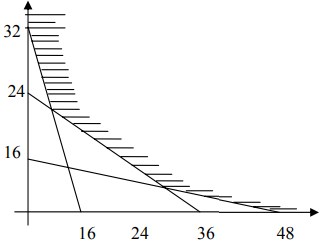
9. Nilai minimum fungsi objektif 5x + 10y pada himpunan penyelesaian sistem pertidaksamaan yang grafik himpunan penyelesaiannya disajikan pada daerah berarsir seperti gambar di bawah adalah …….
A . 410
B . 320
C . 240
D . 200
E . 160
Jawaban : D
Pembahasan :
Terdapat 4 titik ekstrim, yang sudah diketahui 2 titik yaitu titik a (0,32) dan titik d (48,0), tinggal mencari posisi 2 titik ekstrim yang lain
Tentukan persamaan garis:
10. Seorang tukang roti mempunyai bahan A,B dan C masing-masing sebanyak 160 kg, 110 kg dan 150 kg.
Roti I memerlukan 2 kg bahan A, 1 kg bahan B dan 1 Kg bahan C
Roti II memerlukan 1 kg bahan A, 2 kg bahan B dan 3 Kg bahan C
Sebuah roti I dijual dengan harga Rp.30.000 dan sebuah roti II dijual dengan harga Rp.50.000, pendapatan maksimum yang dpat diperoleh tukang roti tersebut adalah…
A. Rp. 8000.000,-
B. Rp. 4500.000,-
C. Rp. 3900.000,-
D. Rp. 3100.000,-
E. Rp. 2900.000,-
Jawaban : D
Pembahasan :
Buat persamaan :
Misal roti I = x dan roti II = y didapat persamaan sbb:
2x + y ≤ 160 …..(1)
x + 2y ≤ 110 …..(2)
x + 3y ≤ 150 ….(3)
buat sketsa grafiknya:
“Sketsa grafik diperlukan untuk melihat daerah himpunan penyelesaian dan titik-titik ekstrim, dibutuhkan skala yang tepat untuk mendapatkan grafik yang optimum (benar atau mendekati kebenaran) untuk memudahkan penyelesaian”
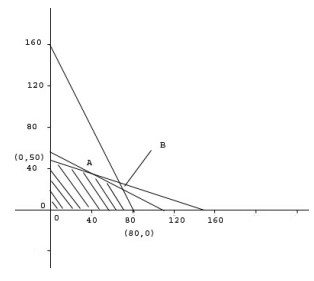
Daerah yang diarsir adalah himpunan penyelesaian dari tiga grafik tsb. Didapat 4 titik ekstrim yaitu (0,50), (80,0), titik A dan titik B
perpotongan (1) dan (2) → titik B
11 – 20 Contoh Soal Program Linear dan Jawaban
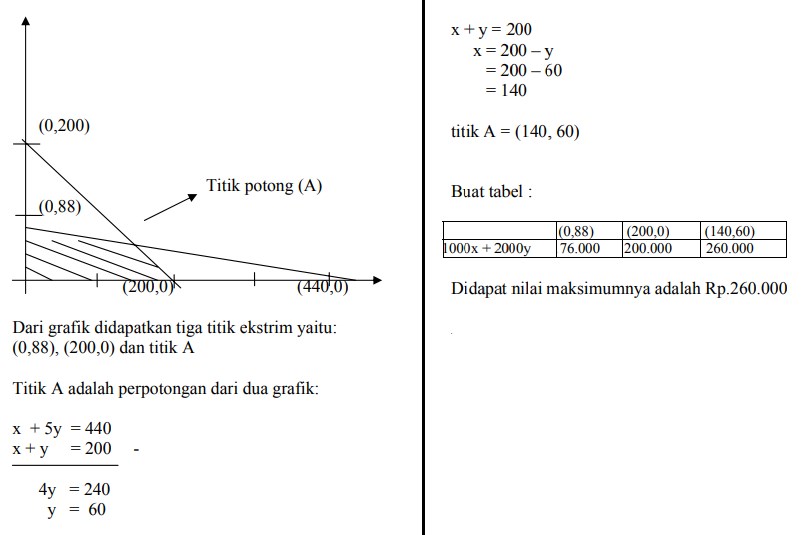
11. Luas daerah parkir 1.760 m² . Luas rata-rata untuk mobil kecil 4 m² dan mobil besar 20 m² . Daya tampung maksimum hanya 200 kendaraan, biaya parker mobil kecil Rp. 1000/jam dan mobil besar Rp.2000/jam. Jika dalam satu jam terisi penuh dan tidak ada kendaraan yang pergi dan dating, maka hasil maksimum tempat parkir itu adalah:
A. Rp.176.000,-
B. Rp. 200.000,-
C. Rp.260.000,-
D. Rp. 300.000,-
E. Rp.340.000,-
Jawaban : C
Pembahasan :
Dibuat persamaan-persamaannya terlebih dahulu:
Misal mobil kecil = x dan mobil besar = y
4 x + 20 y ≤ 1760
x + 5y ≤ 440 …..(1)
x + y ≤ 200 ….(2)
nilai maksimum 1000x + 2000y = ?
buat sketsa grafiknya:
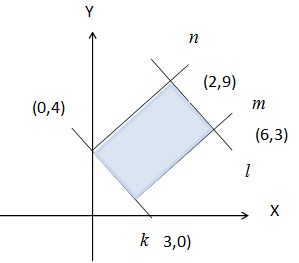
12. Tentukan sistem pertidaksamaan linear dari daerah yang diarsir pada gambar berikut ini!
Jawaban :
Garis k terdiri dari titik (3,0) dan (0,4) maka garisnya adalah :
13. Tentukan nilai maksimum dari 3x + 2y yang memenuhi x + y ≤ 5 , x ≥ 0 , y ≥ 0, dan x , y ∈ R.
Jawaban :
Jadi, nilai maksimum dicapai pada titik (5,0) yaitu: 3 . 5 + 2 . 0 = 15.
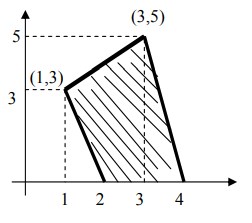
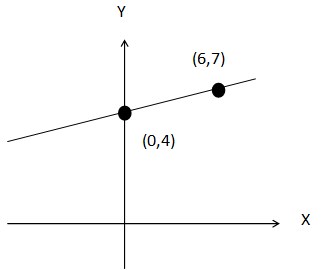
14. Perhatikan Grafik berikut :
Persamaan garis yang melalui 2 titik (0,4) dan (5,7) adalah . . .
Jawaban :
15. Aini, Nia, dan Nisa pergi bersama-sama ke toko buah. Aini membeli 2 kg apel, 2 kg anggur, dan 1 kg jeruk dengan harga Rp 67.000,00. Nia membeli 3 kg apel, 1 kg anggur, dan 1 kg jeruk dengan harga Rp 61.000,00. Nisa membeli 1 kg apel, 3 kg anggur, dan 2 kg jeruk dengan harga Rp. 80.000,00. Tentukan harga 1 kg apel, 1 kg anggur, dan 4 kg jeruk.
Jawaban :
Pembahasan :
Misalkan :
apel = x
anggur = y
jeruk = z
Dari soal, dapat disusun sistem persamaan linear sebagai berikut :
1). 2x + 2y + z = 67.000
2). 3x + y + z = 61.000
3). x + 3y + 2z = 80.000
Ditanya : x + y + 4z = …?
Untuk menjawab pertanyaan seperti ini umumnya yang harus kita cari terlebih dahulu adalah harga satuan masing-masing barang.
Baca Juga 20+ Soal Persamaan Trigonometri
16. Pada sebuah toko buku, Ana membeli 4 buku, 2 pulpen dan 3 pensil dengan harga Rp 26.000,00. Lia membeli 3 buku, 3 pulpen, dan 1 pensil dengan harga 21.000,00. Nisa membeli 3 buku dan 1 pensil dengan harga Rp. 12.000,00. Jika Bibah membeli 2 pulpen dan 3pensil, maka tentukan biaya yang harus dikeluarkan oleh Bibah.
Jawaban :
Pembahasan :
misalkan :
buku = x
pulpen = y
pensil = z
Dari soal, dapat disusun sistem persamaan linear sebagai berikut :
1). 4x + 2y + 3z = 26.000
2). 3x + 3y + z = 21.000
3). 3x + z = 12.000
Ditanya : 2y + 3z = ….?
Untuk menjawab pertanyaan seperti ini umumnya yang harus kita cari terlebih dahulu adalah harga satuan masing-masing barang. Karena yang ditanya harga 2y + 3z, maka kita hanya perlu mencari harga satuan y dan z.
Dari 3x + 3y + z = 21.000 dan 3x + z = 12.000, diperoleh harga satuan pulpen yaitu :
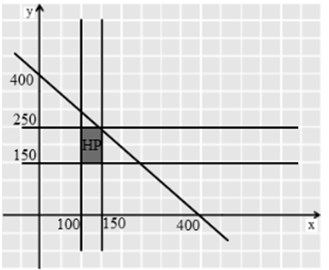
17. Seorang pemilik toko sepatu ingin mengisi tokonya dengan sepatu laki-laki paling sedikit 100 pasang dan sepatu wanita paling sedikit 150 pasang. Toko tersebut hanya dapat menampung 400 pasang sepatu. Keuntungan setiap pasang sepatu laki-laki adalah Rp 10.000,00 dan keuntungan setiap pasang sepatu wanita adalah Rp 5.000,00. Jika banyaknya sepatu laki-laki tidak boleh melebihi 150 pasang, maka tentukanlah keuntungan terbesar yang dapat diperoleh oleh pemilik toko.
Jawaban :
Pembahasan :
Pada soal ini, untuk mengetahui keuntungan terbesar maka yang menjadi fungsi tujuan atau fungsi objektifnya adalah keuntungan penjualan sepatu. Jadi fungsi tujuannya adalah :
F(x,y) = 10.000x + 5.000y
Dengan pemisalan :
sepatu laki-laki = x
sepatu perempuan = y
Sistem pertidaksamaan untuk soal tersebut adalah sebagai berikut :
x + y ≤ 400
100 ≥ x ≤ 150
150 ≥ y ≤ 250
Karena maksimum sepatu laki-laki hanya 150 pasang, maka maksimum sepatu perempuan = 400 – 150 = 250.
Dari sistem pertidaksamaan tersebut, maka diperoleh grafik sebagai berikut :
Dari grafik jelas telihat bahwa keuntungan maksimum berada pada titik pojok paling atas yaitu titik (150,250). Maka nilai maksimum dari fungsi tujuan F(x,y) = 10.000x + 5000y adalah :
F(150,250) = 150 (10.000) + 250 (5.000) = 2.750.000
Jadi, keuntungan terbesar yang dapat diperoleh pemilik toko adalah Rp 2.750.000,00
18. Seorang pembuat kue mempunyai 8 kg tepung dan 2 kg gula pasir. Ia ingin membuat dua macam kue yaitu kue dadar dan kue apem. Untuk membuat kue dadar dibutuhkan 10 gram gula pasir dan 20 gram tepung sedangkan untuk membuat sebuah kue apem dibutuhkan 5 gram gula pasir dan 50 gram tepung. Jika kue dadar dijual dengan harga Rp 300,00/buah dan kue apem dijual dengan harga Rp 500,00/buah, tentukanlah pendapatan maksimum yang dapat diperoleh pembuat kue tersebut.
Jawaban :
Pembahasan
Untuk mengetahui pendapatan maksimum, maka terlebih dahulu kita menyusun sistem pertidaksamaan dan fungsi tujuan dari soal cerita tersebut. Karena yang ditanya pendapatan maksimum, maka tentu harga jual kue merupakan fungsi tujuan pada soal ini. Untuk menyusun sistem pertidaksamaan, yang perlu kita lakukan adalah menentukan variabel dan koefisiennya.
Bahan yang tersedia:
Tepung = 8 kg = 8000 g
Gula = 2 kg = 2000 g
Misalkan :
kue dadar = x
kue apem = y
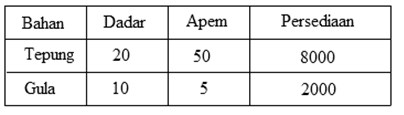
Maka jumlah tepung, gula, dan harga jual merupakan koefisien. Agar lebih mudah, kita dapat memasukkan data yang ada pada soal ke dalam bentuk tabel seperti berikut :
Dari tabel di atas dapat disusun sistem pertidaksamaan sebagai berikut :
20x + 50y = 800 → 2x + 5y ≤ 800
10x +5y = 2000 → 2x + y ≤ 400
x ≥ 0 dan y ≥ 0
dengan fungsi tujuan f(x,y) = 300x + 500y
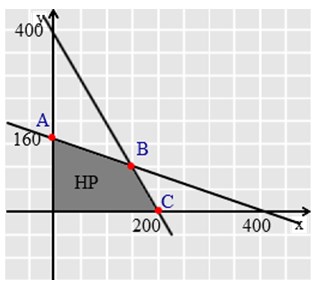
Kemudian gambarkan sistem pertidaksamaan yang sudah disusun dalam grafik.
Untuk garis 2x + 5y = 800
x = 0, y = 160 → (0, 160)
y = 0, x = 400 → (400, 0)
Untuk garis 2x + y = 400
x = 0, y = 400 → (0, 400)
y = 0, x = 200 → (200, 0)
Titik B merupakan titik potong garis 2x + 5y = 800 dengan garis 2x +
y = 400
2x + y = 400
y = 400 – 2x
Dengan metode substitusi :
2x + 5y = 800
2x + 5(400 – 2x) = 800
2x + 2000 – 10x = 800
-8x = -1200
x = 150
Karena x = 150, maka :
y = 400 – 2x
y = 400 – 2(150)
y = 400 – 300
y = 100
Dengan demikian titik B (150, 100)
Selanjutnya substitusikan titik A, B, dan C ke fungsi tujuan :
A(0, 160) → F(x,y) = 300(0) + 500(160) = 80.000
B(150, 100) → F(x,y) = 300(150) + 500(100) = 95.000
C(200, 0) → F(x,y) = 300(200) + 500(0) = 60.000
Jadi, pendapatan maksimum yang bisa diperoleh pedagang kue itu adalah Rp 95.000,00.
19. Menjelang hari raya Idul Adha, Pak Mahmud hendak menjual sapi dan kerbau. Harga seekor sapi dan kerbau di Medan berturut-turut Rp 9.000.000,00 dan Rp 8.000.000,00. Modal yang dimiliki pak Mahmud adalah Rp 124.000.000,00. Pak Mahmud menjual sapi dan kerbau di Aceh dengan harga berturut-turut Rp 10.300.000,00 dan Rp 9.200.000,00. Kandang yang ia miliki hanya dapat menampung tidak lebih dari 15 ekor. Agar mencapai keuntungan maksimum, tentukanlah banyak sapi dan kerbau yang harus dibeli pak Mahmud.
Jawaban :
Pembahasan :
Karena ditanya keuntungan, tentu fungsi tujuannya adalah besar keuntungan dari penjualan sapi dan kerbau. Untuk itu, tentukan terlebih dahulu keuntungan menjual sapi dan kerbau sebagai berikut :
untung sapi = Rp 10.300.000,00 – Rp 9.000.000,00 = Rp 1.300.000,00
untung kerbau = Rp 9.200.000,00 – Rp 8.000.000,00 = Rp 1.200.000,00
Misalkan banyak sapi = x dan banyak kerbau = y, maka fungsi tujuan menjadi :
F(x,y) = 1.300.000x + 1.200.000y
Model matematika yang memenuhi soal adalah :
x ≥ 0 → banyak sapi tidak mungkin negatif
y ≥ 0 → banyak kerbau tidak mungkin negatif
x + y ≤ 15 → karena kandang hanya dapat menampung 15 ekor.
Karena modal Pak Mahmud Rp 124.000.000,00 maka :
9.000.000x + 8.000.000y ≤ 124.000.000 → disederhanakan menjadi :
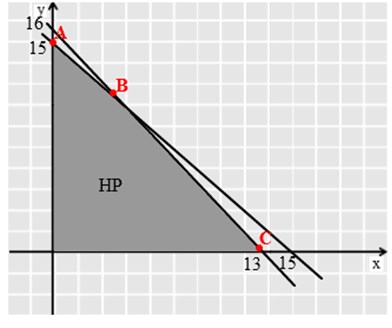
9x + 8y ≤ 124Selanjutnya, kita tentukan titik koordinat masing-masing garis agar dapat kita gambar dalam grafik.
Untuk x + y = 15
jika x = 0, maka y = 15 → (0,15)
jika y = 0, maka x = 15 → (15,0)
Untuk 9x + 8y = 124
Jika x = 0, maka y = 15,5 → (0, 16) → digenapkan karena jumlah sapi tidak mungkin 1/2.
jika y = 0, maka x = 13,7 → (13 ,0) → digenapkan menjadi 13
karena melihat kondisi grafik, titik ini akan menjadi titik pojok, jadi 13,7 tidak digenapkan ke 14 karena jika dibulatkan ke 14 maka akan lebih dari Rp 124.000.000,00.
Dari grafik di atas dieproleh tiga titik pojok yang memenuhi syarat untuk menghasilkan nilai maksimum yaitu titik A, B, dan C. Titi A dan C dapat ditentukan secara langsung yaitu A(0,15) dan C(13,0). Titik B merupakan titik potong antara garis x + y = 15 dan 9x + 8y = 124.
x + y = 15 , maka x = 15 – y → substitusi ke persamaan 9x + 8y = 124
9(15 – y) + 8y = 124
135 – 9y + 8y = 124
y = 11
x + y = 15
x + 11 = 15
x = 4 → jadi titik B(4,11)
Selanjutnya substitusi masing-masing titik ke fungsi tujuan :
A(0,15) → f(x,y) = 1.300.000(0) + 1.200.000(15) = 18.000.000
B(4,11) → f(x,y) = 1.300.000(4) + 1.200.000(11) = 18.400.000
C(13,0) → f(x,y) = 1.300.000(13) + 1.200.000(0) = 16.900.000
Jadi, agar keuntungannya maksimum, jumlah sapi dan kerbau yang harus dibeli pak Mahmud adalah 4 ekor sapi dan 11 ekor kerbau.
20. Seorang pedagang menjual buah mangga dan pisang dengan menggunakan gerobak. Pedagang tersebut membeli mangga dengan harga Rp 8.000,00/kg dan pisang Rp 6.000,00/kg. Modal yang tersedia Rp 1.200.000,00 dan gerobaknya hanya dapat menampung mangga dan pisang sebanyak 180 kg. Jika harga jual mangga Rp 9.200,00/kg dan pisang Rp 7.000,00/kg, maka tentukanlah laba maksimum yang diperoleh pedagang tersebut.
Jawaban :
Pembahasan :
Karena ditanya laba maksimum, maka fungsi tujuannya adalah keuntungan dari menjual buah mangga dan buah pisang perkilonya.
Berikut untung penjualan :
mangga = 9.200 – 8.000 = 1.200
pisang = 7.000 – 6000 = 1.000
misalkan :
mangga = x
pisang = y
maka fungsi tujuannya adalah :
F(x,y) = 1.200x + 1.000y
Model matematika atau sistem pertidaksamaan yang memenuhi soal tersebut adalah :
x + y ≤ 180
8.000x + 6.000y ≤ 1.200.000 → 4x + 3y ≤ 600
x ≥ 0
y ≥ 0
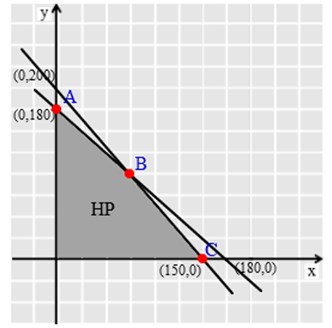
Titik potong masing-masing garis terhadap sumbu x dan sumbu y : Garis x + y = 180
untuk x = 0 , y = 180 → (0, 180)
untuk y = 0, x = 180 → (180,0)
Garis 4x + 3y = 600
untuk x = 0, y = 200 → (0, 200)
untuk y = 0, x = 150 → (150, 0)
Himpunan penyelesaian sistem pertidaksamaan adalah :
Dari grafik diketahui ada tiga titik pojok yaitu A, B, dan C. Titik C merupakan perpotongan antara garis x + y = 180 dengan 4x + 3y = 600.
Substitusi titik pojok pada fungsi objektif F(x,y) 1.200x + 1.000y :
A (0, 180) → F(x,y) =1.000(180) = 180.000
B (60, 120) → F(x,y) = 1.200(60) + 1.000(120) = 192.000
C (150,0) → F(x,y) = 1.200(150) = 180.000
Jadi laba maksimum yang diperoleh pedagang buah adalah Rp 192.000,00.
21 – 25 Soal Program Linear dan Pembahasan
Soal Cerita
21. Ibu Leni akan membuat 2 jenis roti dengan menggunakan bahan tepung 300 gram dan mentega 20 gram untuk jenis A. Sedangkan untuk jenis B digunakan bahan 200 gram tepung dan 60 gram mentega. Jika bahan yang tersedia 3 kg tepung dan 1,2 kg mentega
a) Ubahlah permasalahan tersebut ke dalam model matematika!
b) Gambarkanlah grafik daerah himpunan penyelesaian dari permasalahan tersebut, lengkap dengan langkah-langkah penyelesaiannya!
Jawaban :
Pembahasan :
Memahami masalah
Diketahui :
Ada dua jenis roti
Jenis A menggunakan bahan tepung 300 gram dan mentega 20 gram
Jenis B menggunakan bahan tepung 200 gram dan mentega 60 gram
Bahan yang tersedia 3 kg tepung dan 1,2 kg mentegaa) ubahlah permasalahan tersebut kedalam model matematikanya!
Jawaban :
b) Menggambarkan daaerah penyelesaian:
Ambil titik uji P (0,0), akan diperoleh hubungan:
Titik uji P (0,0) untuk persamaan 3x + 2y = 30 diperoleh hubungan:
3x + 2y ≤ 30 => 3 (0) – 2 (0) ≤ 30
=> 0 – 0 ≤ 30
=> 0 ≤ 30 (benar)
Berarti daerah tempat titik P (0,0) merupakan daerah penyelesaian
Titik uji P (0,0) untuk persamaan x + 3y = 60 diperoleh hubungan:
x + 3y ≤ 60 => 0 – 3 (0) ≤ 60
=> 0 – 0 ≤ 60
=> 0 ≤ 60 (benar)
Berarti daerah tempat titik P (0,0) merupakan daerah penyelesaian
Menentukan daerah penyelesaian x ≥ 0 dan y ≥ 0
x ≥ 0, gambar garisnya berimpit dengan y dengan daerah penyelesaian dikanan sumbu y
y ≥ 0, gambar garisnya berimpit dengan x dengan daerah penyelesaian dikanan sumbu x
Gambar grafik
22. Seorang petani ingin memberikan pupuk pada tanaman padi. Pupuk yang diberikan harus mengandung sekurang-kurangnya 600 g fosfor dan 720 g nitrogen. Pupuk I mengandung 30 g fosfor dan 30 g nitrogen per bungkus. Pupuk II mengandung 20 g fosfor dan 40 g nitrogen per bungkus. Petani itu ingin mencampur kedua pupuk tersebut. Satu bungkus pupuk I harganya Rp 17.500,00 dan pupuk II harganya Rp 14.500,00 per bungkus.
a) Ubahlah permasalahan tersebut ke dalam model matematikanya!
b) Gambarkanlah grafiknya!
Jawaban :
Pembahasan :
Memahami masalah
Diketahui:
Pupuk I mengandung 30 g fosfor dan 30 g nitrogen per bungkus
Pupuk II mengandung 20 g fosfor dan 40 g nitrogen per bungkus
Pupuk harus mengandung sekurang-kurangnya 600 g fosfor dan 720 g
nitrogen Satu bungkus pupuk I harganya Rp 17.500,00 dan pupuk II hargnya Rp14.500,00 perbungkusa) Ubahlah permasalahan tersebut ke dalam model matematikanya!
b. Menggambarkan grafiknya
Diketahui persamaan 3x + 2y ≥ 60 dan 3x + 4y ≥ 72
Untuk 3x + 2y ≥ 60
Menentukan titik potong pada sumbu x dan y
Untuk y = 0 => 3x + 2(0) = 60
3x = 60
x = 20 => (20, 0)
Untuk x = 0 => 3(0) + 2y = 60
2y = 60
y = 30 => (0, 30)
Untuk 3x + 4y ≥ 72
Menentukan titik potong pada sumbu x dan y
Untuk y = 0 => 3x + 4(0) = 72
3x = 72
x = 24 => (24, 0)
Untuk x = 0 => 3(0) + 4y = 72
4y = 72
y = 18 => (0, 18)
dapat diperoleh grafik
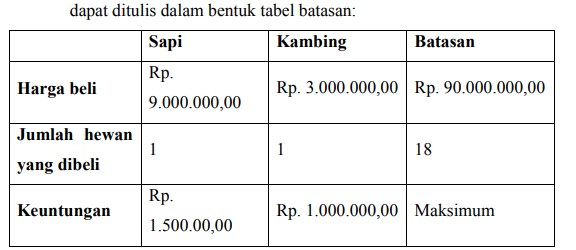
23. Menjelang hari raya Idul Adha pak Andi hendak menjual sapi dan kambing. Harga seekor sapi adalah Rp. 9.000.000,00 dan harga seekor kambing adalah Rp. 3.000.000,00. Modal yang dimiliki pak Anto adalah Rp. 90.000.000,00. Keuntungan yang didapat pak Andi dari penjualan seekor sapi adalah Rp. 1.500.000,00 sedangkan keuntungan yang didapat dari penjualan sesekor kambing adalah Rp. 1.000.000,00. Kandang yang ia miliki hanya dapat menampung tidak lebih dari 18 ekor binatang. Agar mencapai keuntungan maksimum, tentukanlah banyak sapi dan kambing yang harus dibeli pak Andi!
Jawaban :
Pembahasan :
Memahami masalah
diketahui:
Harga seekor sapi adalah Rp. 9.000.000,00
Harga seekor kambing adalah Rp. 3.000.000,00
Modal yang dimiliki pak Anto adalah Rp. 90.000.000,00. Keuntungan yang didapat pak anto dari penjualan seekor sapi adalah Rp. 1.500.000,00 Sedangkan keuntungan yang didapat dari penjualan sesekor kambing adalah Rp. 1.000.000,00. Kandang yang ia miliki hanya dapat menampung tidak lebih dari 18 ekor binatang.
Ditanya : Agar mencapai keuntungan maksimum, tentukanlah banyak sapi dan kambing yang harus dibeli pak Anto!
menyusun rencana penyelesaian masalah
- mendefinisikan variabel
- menentukan fungsi obyektif
- menyusun model matematika dari setiap kendala yang ada
- persyaratan non negatif
- Mengambar daerah penyelesaian yang memenuhi kendala
- Menentukan titik-titik pojok dari daerah penyelesaian.
- Mensubstitusikan masing-masing titik pojok ke fungsi obyektif.
- Memilih titik yang menjadikan nilai fungsi obyektif menjadi maksimum
melaksanakan rencana penyelesaian masalah
mendefinisikan variabel
Misal:
x = sapi
y = kambing
menentukan fungsi obyektif
Keuntungan yang didapat pak anto dari penjualan seekor sapi adalah Rp. 1.500.000,00 Sedangkan keuntungan yang didapat dari penjualan sesekor kambing adalah Rp. 1.000.000,00. Fungsi obyektif/fungsi tujuan : Z = 1.500.000x + 1.000.000y
menyusun model matematika dari setiap kendala yang ada
Harga seekor sapi adalah Rp. 9.000.000,00 sedangkan harga seekor kambing adalah Rp. 3.000.000,00. Modal yang dimiliki pak Anto adalah Rp. 100.000.000,00.
Kendala 1 : 9.000.000x + 3.000.000y ≤ 90.000.000 => 9x + 3y ≤ 90
Kandang yang ia miliki hanya dapat menampung tidak lebih dari 18 ekor binatang.
Kendala 2 : x + y ≤ 18
persyaratan non negatif
x ≥ 0
y ≥ 0
menggambarkan daerah penyelesaian dari masalah tersebut.
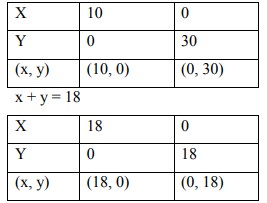
9x + 3y = 90
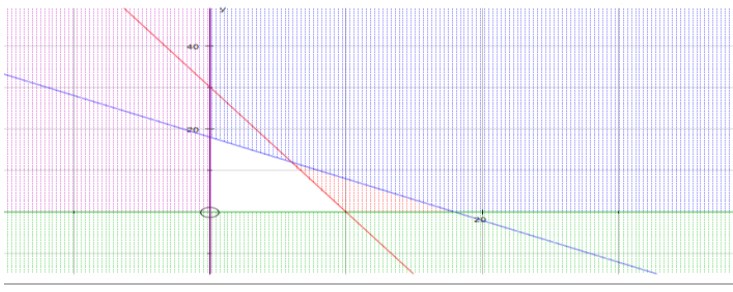
Gambar grafik:
Untuk mencari titik potong garis 9x + 3y = 90 dan garis x + y = 18 menggunakan cara eliminasi-substitusi:
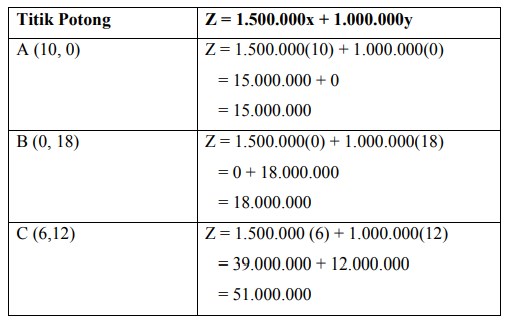
Menentukan titik-titik pojok dari daerah penyelesaian berdasarkan gambar, maka didapat 3 titik pojok, yaitu : (10,0), (0,18), dan (6,12)
Mensubstitusikan masing-masing nilai pojok ke fungsi obyektif
Memilih titik yang menjadi nilai fungsi obyektif menjadi nilai maksimum titik yang menjadikan nilai fungsi obyektif menjadi nilai maksimum adalah titik C (6,12).
Jadi, agar keuntungannya maksimum maka jumalah sapi dan kambing yang harus dibeli pak Anto adalah 6 ekor sapi dan 12 ekor kambing.
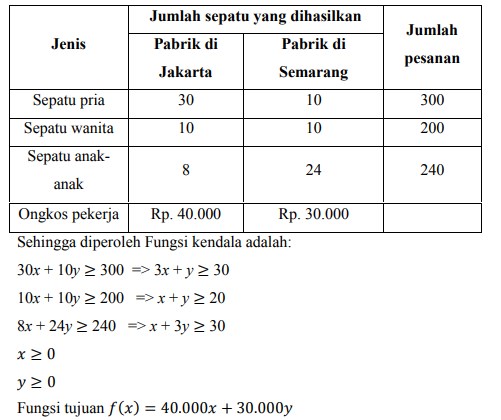
24. Seorang pengusaha mempunyai pabrik sepatu di dua kota, yaitu di kota Jakarta dan Semarang. Untuk memenuhi pemesanan sebanyak 300 sepatu pria, 200 sepatu wanita dan 240 sepatu anak-anak. Maka pengusaha tersebut mengoperasikan kedua pabrik tersebut. Pabrik Jakarta setiap hari menghasilkan sepatu pria, sepatu wanita dan sepatu anak-anak yang masing-masing 30, 10, dan 12 dengan ongkos pekerja Rp 40.000,00/hari. Pabrik di Semarang setiap hari menghasilkan sepatu pria, sepatu wanita, dan sepatu anak-anak yang masing-masing 8, 10, dan 24 dengan ongkos pekerja Rp 30.000,00/ hari.
a. Ubahlah permasalahan tersebut ke dalam model matematikanya!
b. Gambarkanlah grafiknya!
c. Tentukan biaya total minimum untuk ongkos pekerja perusahaan tersebut!
Jawaban :
Pembahasan :
Memahami masalah
Diketahui:
Pabrik di Jambi setiap hari menghasilkan sepatu pria, sepatu wanita dan sepatu anak-anak masing-masing 30, 10, dan 12 dengan ongkos pekerja Rp. 40.000/hari.
Pabrik di Solo setiap hari menghasilkan sepatu pria, sepatu wanita dan sepatu anak-anak masing-masing 8, 10, dan 24 dengan ongkos pekerja Rp. 30.000/hari.
Jumlah pesanan sebanyak 300 sepatu pria, 200 sepatu wanita, dan 240 sepatu anak-anak.
Ditanya:
a. Ubahlah permasalahan tersebut ke dalam model matematikanya!
b. Gambarkanlah grafiknya!
c. Tentukan biaya total minimum untuk ongkos pekerja perusahaan tersebut!
Jawab :
menyusun rencana penyelesaian masalah
- mendefinisikan variabel
- menentukan fungsi obyektif
- menyusun model matematika dari setiap kendala yang ada
- persyaratan non negatif
- Mengambar daerah penyelesaian yang memenuhi kendala
- Menentukan titik-titik pojok dari daerah penyelesaian.
- Mensubstitusikan masing-masing titik pojok ke fungsi obyektif.
- Memilih titik yang menjadikan nilai fungsi obyektif menjadi minimum
Melaksanakan rencana penyelesaian masalah
Misalkan :
x = Pabrik di Jambi
y = Pabrik di Solo
a) permasalahan diatas dapat dituangkan dalam tabel seperti berikut :
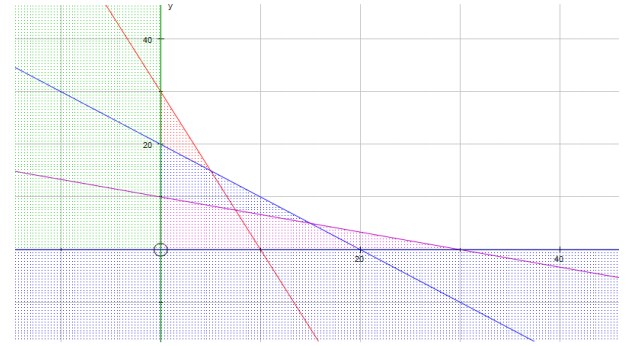
b) Menggambarkan grafiknya
dapat diperoleh grafik
c) biaya total minimum untuk ongkos pekerja perusahaan
Untuk mencari biaya minimum yang harus dikeluarkan, maka kita tentukan terlebih dahulu titik potong antara dua garis dengan eliminasi.
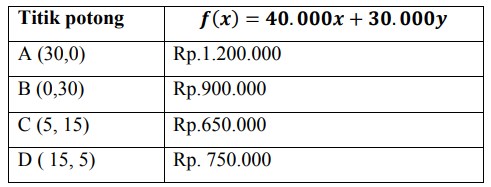
dengan menguji metode titik pojok, diketahui pengeluaran minimum dengan tabel sebagai berikut:
Sehingga diperoleh, total pengeluaran minimum dari perusahaan tersebut adalah Rp.650.000, pada titik potong C (5, 15).
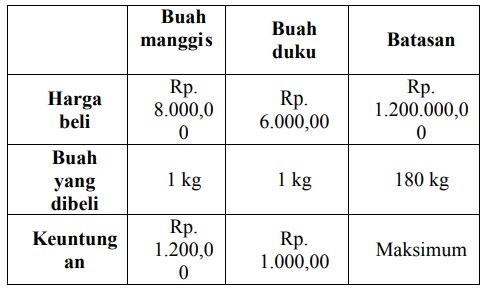
25. Bapak Darman adalah seorang pedagang buah di kota Binjai yang mempunyai modal sebesar Rp. 1.200.000,00. Ia membeli buah manggis dengan harga Rp. 8.000,00/kg dan buah duku dengan harga Rp. 6.000,00/kg. gerobak dagangan pak darman hanya dapat menampung buah manggis dan duku sebanyak 180 kg. jika keuntungan penjualan buah manggis adalah Rp. 1.200,00/kg dan buah duku sebesar Rp. 1.000,00/kg, maka tentukan keuntungan maksimum yang diperoleh bapak Darman!
Jawaban :
Pembahasan :
memahami masalah
diketahui:
harga buah manggis yang dibeli adalah Rp. 8.000,00/kg, sedangkan harga buah duku yang dibeli adalah Rp. 6.000,00/kg. modal yang dimiliki bapak darman sebanyak Rp. 1.200.000,00. Keuntungan dari penjualan buah manggis adalah Rp. 1.200,00/kg sedangkan keuntungan dari penjualan buah duku adalah Rp. 1.000,00/kg. Gerobak dagangan bapak darman hanya dapat menampung buah manggis dan buah duku sebanyak 180 kg.
dapat ditulis dalam bentuk tabel batasan:
Ditanya :
Jika keuntungan penjualan buah manggis adalah Rp. 1.200,00/kg dan buah duku sebesar Rp. 1.000,00/kg, maka tentukan keuntungan maksimum yang diperoleh bapak Darman!
menyusun rencana penyelesaian masalah
- mendefinisikan variabel
- menentukan fungsi obyektif
- menyusun model matematika dari setiap kendala yang ada
- persyaratan non negatif
- Mengambar daerah penyelesaian yang memenuhi kendala
- Menentukan titik-titik pojok dari daerah penyelesaian.
- Mensubstitusikan masing-masing titik pojok ke fungsi obyektif.
- Memilih titik yang menjadikan nilai fungsi obyektif menjadi maksimum.
melaksanakan rencana penyelesaian masalah
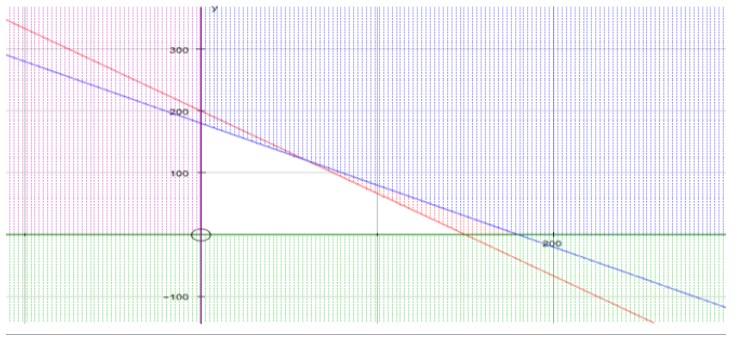
Dapat diperoleh grafik
Maka :
Jadi, keuntungan terbesar yang diperoleh bapak darman adalah sebesar Rp. 192.000,00.
Sudah selesai membaca dan berlatih Soal Program Linear ini ? Ayo lihat dulu Soal Matematika lainnya









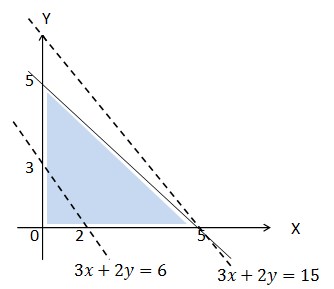
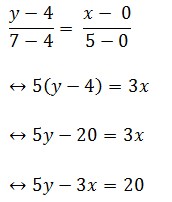


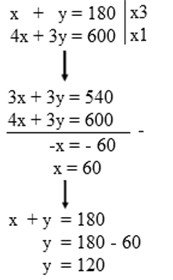



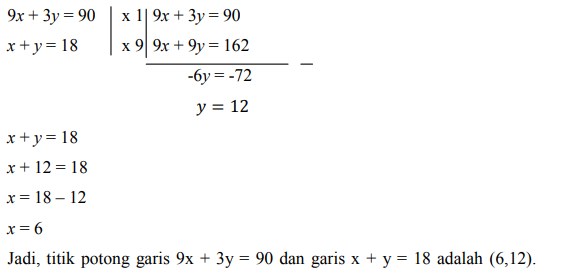







TERIMAKASIH BANYAK 👍👍👍👍
TERIMA KASIH IZIN DOUWNLOAD, MOHON BISA DIKIRIM METERI LEWAT EMAIL INI, SEMOGA JADI AMAL BAIK SDR KU