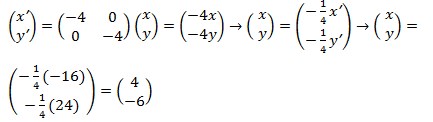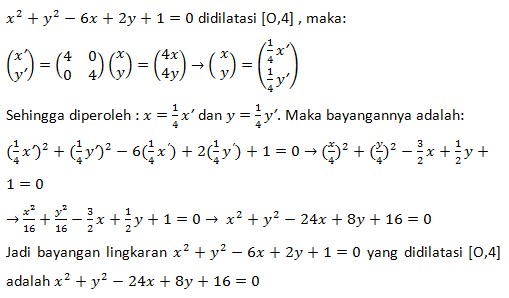Contoh Soal Refleksi dan Dilatasi dan Jawaban – Transformasi merupakan suatu pemetaan titik pada suatu bidang ke himpunan titik pada bidang yang sama. Jenis-jenis dari transformasi yang dapat dilakukan antara lain :
Translasi (Pergeseran) : Translasi merupakan salah satu jenis transformasi yang berguna untuk memindahkan suatu titik sepanjang garis lurus dengan arah dan jarak.
Refleksi (Pencerminan) : Rotasi merupakan pencerminan atau yang biasa kita kenal dengan sebutan refleksi. Sama halnya dengan bayangan benda yang terbentuk pada sebuah cermin. Suatu objek yang mengalami refleksi akan mempunyai bayangan benda yang dihasilkan oleh suatu cermin.
Rotasi (Perputaran) : Rotasi atau perputaran merupakan suatu perubahan kedudukan atau posisi objek dengan cara diputar lewat suatu pusat dan sudut tertentu.
Dilatasi (Penskalaan) : Dilatasi merupakan perbesaran atau pengecilan sebuah objek.

1 – 12 Contoh Soal Refleksi dan Dilatasi dan Jawaban
1. ABCD adalah sebuah persegi dengan koordinat titik-titik sudut A(1,1), B(2,1), C(2,2) dan D(1,2). Tentukan peta atau bayangan dari titik-titik sudut persegi itu oleh dilatasi [O,2]!
A. A’(2,2), B’(4,3), C’(4,4) dan D’(2,4)
B. A’(2,2), B’(4,2), C’(4,4) dan D’(2,3)
C. A’(2,2), B’(4,3), C’(4,4) dan D’(2,3)
D. A’(2,2), B’(4,2), C’(4,4) dan D’(2,4)
Jawaban : D
Pembahasan :
Jadi peta dari titik-titik sudut ABCD adalah A’(2,2), B’(4,2), C’(4,4) dan D’(2,4)
2. Jika titik A(15,8) dicerminkan terhadap garis x = 7, maka bayangan titik A adalah titik A’ dengan koordinat….
A. A’(-1,8)
B. A’(1,8)
C. A’(1,-8)
D. A’(-1,-8)
Jawaban : A
Pembahasan :
Jadi bayangan titik A(15,8) dicerminkan terhadap garis x adalah A’(-1,8)
3. Titik A(a,b) dicerminkan terhadap garis x = 2 menghasilkan bayangan titik A’(0,2), maka nilai (a,b) adalah….
A. (4,2)
B. (2,4)
C. (4,1)
D. (1,4)
Jawaban : A
Pembahasan :
Sehingga didapat bahwa nilai (a, b) adalah (4,2)
4. Titik A’(-16,24) merupakan bayangan dari titik A(x,y) yang didilatasikan dengan pusat O(0,0) dan faktor skala -4. Koordinat titik A adalah….
Jawaban :
Pembahasan :
Jadi titik A’(-16,24) merupakan bayangan dari titik A(4,-6) yang didilatasikan dengan pusat O(0,0) dan faktor skala -4.
5. Tentukan persamaan peta dari garis 3x – 5y + 15 = 0 oleh pencerminan terhadap sumbu !
Jawaban :
Pembahasan :
6. Tentukan persamaan peta dari garis 3x – 5y + 15 = 0 oleh dilatasi terhadap pusat O(0,0) dengan faktor skala 5!
Jawaban :
Pembahasan :
Simak Juga : Contoh Soal Himpunan
7. Lingkaran x2 + y2– 6x + 2y + 1 = 0. Jika ditransformasikan dengan dilatasi [O,4], persamaan bayangannya adalah….
Jawaban :
Pembahasan :
8. Diketahui titik P(12,-5) dan A(-2,1). Bayangan titik P oleh dilatasi [A,½]adalah….
Jawaban :
Pembahasan :
9. Bayangan titik P(-2,3) oleh dilatasi [O,k] adalah P’(4,-6) sehingga bayangan titik Q(3,-2) oleh [O,4k] adalah….
A. Q’(24,-16)
B. Q’(-24,16)
C. Q’(-24,-16)
D. Q’(24,16)
Jawaban : B
Pembahasan :
10. Tentukan bayangan titik P(-4,5) oleh refleksi terhadap garis y = -x dilanjutkan dengan refleksi terhadap garis x = 2!
Jawaban :
Pembahasan :
Jadi bayangan titik P(-4,5) oleh refleksi terhadap garis dilanjutkan dengan refleksi terhadap garis x = 2 adalah P”(9,4)
11. Tentukan persamaan bayangan lingkaran x2 + y2 – 4x – 20 = 0 oleh refleksi terhadap sumbu dilanjutkan dilatasi [O,2] !
Jawaban :
Pembahasan :
12. Sebuah persamaan lingkaran x2 + y2 – 4x + 6y – 8 = 0 dicerminkan terhadap , maka bayangannya adalah….
Jawaban :
Pembahasan :
Jadi bayangan persamaan lingkaran x2 + y2 – 4x + 6y – 8 = 0 yang dicerminkan terhadap y = x + 3 adalah x2 + y2 + 12x – 10y + 40 = 0
Sudah selesai membaca dan berlatih soal ini ? Ayo lihat dulu Soal Matematika lainnya