Contoh Soal Relasi dan Fungsi dan Jawaban – Relasi Menyatakan hubungan antara suatu anggota himpunan dengan anggota himpunan lainnya. Himpunan A dan himpunan B dikatakan memiliki relasi jika ada anggota himpunan yang saling berpasangan. Fungsi (pemetaan) merupakan relasi dari himpunan A ke himpunan B, jika setiap anggota himpunan A berpasangan tepat satu dengan anggota himpunan B.

Secara Singkat Perbedaan Relasi dan Fungsi:
Relasi adalah hubungan antara anggota dari himpunan satu dengan lainnya
Fungsi adalah relasi khusus yang memasangkan anggota himpunan tepat satu dengan anggota himpunan lainnya.
Relasi
Relasi pada suatu himpunan atau relasi antar dua himpunan dapat pula ditunjukkan dengan diagram.Perhatikan contoh di bawah ini.
Suatu relasi R terdiri dari:
Sebuah himpunan A
Sebuah himpunan B
Suatu kalimat terbuka P(x, y) dimana P(a, b) adalah benar atau salah untuk sebarang pasangan terurut (a, b) yang termasuk dalam A x B.
Beberapa Pengertian Penting :
- Daerah Asal
Daerah asal atau biasa disebut domain suatu relasi adalah himpunan tidak kosong dimana sebuah relasi didefinisikan.
- Daerah Kawan
Daerah kawan atau biasa disebut kodomain suatu relasi adalah himpunan tidak kosong dimana anggota domain memiliki pasangan sesuai relasi yang didefinisikan.
- Daerah Hasil
Daerah hasil atau biasa disebut range suatu relasi adalah sebuah himpunan bagian dari daerah kawan (kodomain) yang anggotanya adalah pasangan anggota domain yang memenuhi relasi yang didefinisikan.
- Hasil Kali Kartesius
Misalkan A dan B dua himpunan. Relasi dari A ke B yang memasangkan setiap anggota himpunan A ke setiap anggota himpunan B disebut hasil kali kartesius A dan B, dan ditulis:
A × B = {(x,y)│ x ∈ A dan y ∈ B}.
Fungsi
Fungsi f adalah suatu relasi yang menghubungkan setiap anggota x dalam suatu himpunan yang disebut daerah asal (Domain) dengan suatu nilai tunggal f(x) dari suatu himpunan kedua yang disebut daerah kawan (Kodomain).
Himpunan nilai yang diperoleh dari relasi tersebut disebut daerah hasil ( Range). Untuk memberi nama suatu fungsi dipakai sebuah huruf tunggal seperti f, g, dan huruf lainnya. Maka f(x), yang di baca “ f dari x “ menunjukkan nilai yang diberikan oleh f
kepada x. Misalkan : f(x) = x+ 2, maka f(3) = 3 + 2.
Sifat-sifat Fungsi :
Fungsi injektif (satu-satu) Jika fungsi f : A → B, setiap b ∈ B hanya mempunyai satu kawan saja di A, maka fungsi itu disebut fungsi satu-satu atau injektif.
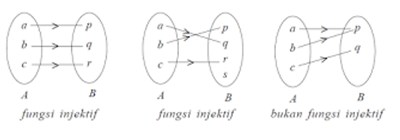
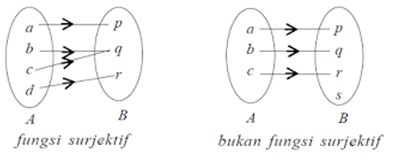
Fungsi surjektif (onto) Pada fungsi f : A → B, setiap b ∈ B mempunyai kawan di A, maka f disebut fungsi surjektif atau onto.
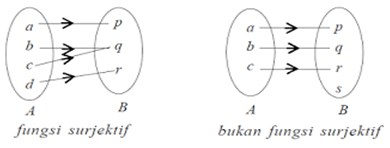
Fungsi bijektif (korespondensi satu-satu) Suatu fungsi yang bersifat injektif sekaligus surjektif disebut fungsi bijektif atau korespondensi satu-satu.
1 – 10 Contoh Soal Relasi dan Fungsi beserta Pembahasan dan Jawaban
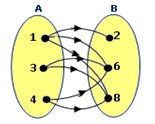
1. Relasi dari himpunan A ke himpunan B pada diagram panah di samping adalah . . .
A. kurang dari
B. setengah dari
C. lebih dari
D. faktor dari
Jawaban : A
Pembahasan :
“kurang dari” :
{(1, 2), (1, 6), (1, 8), (3, 6), (3, 8), (4, 6),(4, 8)}
2. Relasi “factor dari” dari himpunan P = {1, 2, 3} ke Q = {2, 4, 6} ditunjukkan oleh diagram panah ….
Jawaban : C
Pembahasan :
” factor dari ” :
{(1, 2), (1, 4) (1, 6), (2, 2), (2, 4), (2, 6), (3, 6)}
3. K = {3, 4, 5} dan L = {1, 2, 3, 4, 5, 6, 7}, himpunan pasangan berurutan yang menyatakan relasi “dua lebihnya dari” dari himpunan K ke L adalah ….
A. {(3, 5), (4, 6)}
B. {(3, 5), (4, 6), (5, 7)}
C. {(3, 1), (4, 2), (5, 3)}
D. {(3, 2), (4, 2), (5, 2)}
Jawaban : B
Pembahasan :
” dua lebihnya dari ” dri himpunan K ke L :
3 —> 5, 4 —> 6, 5 —> 7 atau
{(3, 5), (4, 6), (5, 7)}
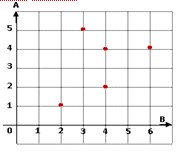
4. Himpunan pasangan berurutan dari grafik catesius di bawah adalah …
A. {(2, 1), (3, 5), (4, 4), (6, 4)}
B. {(1, 2), (2, 4), (4, 6), (5, 3)}
C. {(1, 2), (2, 4), (4, 4), (4, 6), (5, 3)}
D. {(2, 1), (3, 5), (4, 2), (4, 4), (6, 4)}
Jawaban : D
Pembahasan :
Himpunan Pasangan berurutan dari grafik cartesius :
{(2, 1), (3, 5), (4, 2), (4, 4), (6, 4)}
5. Range dari himpunan pasangan berurutan {(2, 1), (3, 5), (4, 2), (4, 4), (6, 4)} adalah …
A. {1, 2, 4, 5}
B. {1, 2, 3, 4, 5}
C. {1, 2, 3, 4, 5, 6}
D. {1, 2, 3, 4, 5, 6}
Jawaban : A
Pembahasan :
Range dari {(2, 1), (3, 5), (4, 2), (4, 4), (6, 4)}
yaitu :
{1, 2, 4, 5}
Simak Juga : Soal Peluang
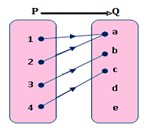
6. Diagram panah pada gambar di bawah merupakan pemetaan maka rangenya adalah. . .
A. {a, b, c}
B. {d, e}
C. {a, b, c, d, e}
D. {1, 2, 3, 4}
Jawaban : A
Pembahasan :
Rangenya adalah {a, b, c}
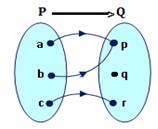
7. Daerah hasil pemetaan yang ditunjukan oleh diagram panah di bawah adalah. . .
A. {a, b, c}
B. b. {p, r}
C. {p, q, r}
D. { a, b, c, p, r}
Jawaban : B
Pembahasan :
Hasil pemetaan dari diagram panah di atas :
{p, r}
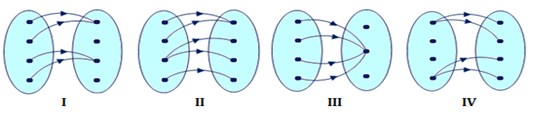
8. Dari gambar diagram panah di dibawah, yang merupakan pemetaan ialah …
A. hanya I dan II
B. hanya II dan III
C. hanyan I dan III
D. hanyan II dan IV
Jawaban : C
Pembahasan :
yang merupakan pemetaan hanya I dan III
9. Dari himpunan pasangan berurutan berikut ini :
I. {(1, 2), (2, 2), (3, 3)}
II. {(1, 2), (2, 2), (3, 1), (3, 2)}
III. {(1, 1), (1, 2), (1, 3), (1, 4)}
IV. {(1, 1), (1, 2), (2, 3), (2, 4)}
Yang merupakan pemetaan adalah …
A. IV
B. III
C. II
D. I
Jawaban : D
Pembahasan :
Yang merupakan pemetaan adalah {(1, 2), (2, 2), (3, 3)}
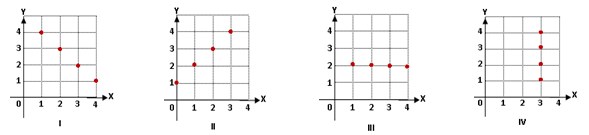
10. Dari diagram cartesius di bawah ini, yang menunjukkan pemetaan adalah ….
Dari diagram cartesius di bawah ini, yang menunjukkan pemetaan adalah ….
A. hanya I, II dan III
B. hanya I, II dan IV
C. hanya I, III dan IV
D. hanya II, III dan IV
Jawaban : A
Pembahasan :
Yang menunjukkan pemetaan hanya I, II dan III
11 – 20 Contoh Soal Relasi dan Fungsi dan Jawaban
11. Diketahui : Himpunan A = {factor dari 10} dan B = {factor prima dari 30}. Banyak semua pemetaan yang mungkin dari himpunan A ke himpunan B adalah …
A. 81
B. 64
C. 16
D. 8
Jawaban : A
Pembahasan :
A = {1, 2, 5, 10} ⇒ n(A) = 4
dan B = {2, 3, 5} ⇒ n(B) = 3
Banyak pemetaan A ⇒ B adalah 34 = 81
12. K = {factor dari 8} dan L = {bilangan prima yang kurang dari 7}. Banyak semua pemetaan yang mungkin dari himpunan K ke himpunan L adalah …
A. 100
B. 81
C. 64
D. 16
Jawaban : B
Pembahasan :
K = {1, 2, 4, 8} ⇒ n(K) = 4
L = {2, 3, 5} ⇒ n(L) = 3
n(K ⇒ L) = 34 = 81
13. Diketahui : P = {x| 11 < x <19, x bil. Prima}, Q = { y| y2< 9, y bil. Cacah}, banyak semua pemetaan yang mungkin dari himpunan P ke himpunan Q adalah …
A. 27
B. 8
C. 4
D. 2
Jawaban : C
Pembahasan :
P = {13, 17} ⇒ n(P) = 2
Q = {1, 2} ⇒ n(Q) = 2
n(P ⇒ Q) = 2² = 4
14. Banyak koresponden satu-satu yang mungkin terjadi dari himpunan P ={3, 5, 7, 9} dan Q = {p, q, r, s} adalah …
A. 4 cara
B. 8 cara
C. 16 cara
D. 24 cara
Jawaban : D
Pembahasan :
Banyaknya koresponden satu-satu :
4! = 1.2.3.4 =24 cara
15. Jika n(P) = n(Q) = 3 , maka banyaknya koresponden satu-satu antara himpunan P ke Q adalah
A. 15 cara
B. 12 cara
C. 9 cara
D. 6 cara
Jawaban : D
Pembahasan :
3! = 1.2.3 = 6 cara
Lihat Juga : Soal Kesebangunan dan Kekongruenan
16. Dari pernyataan-pernyataan berikut :
I. Siswa dengan tempat duduknya
II. Siswa dengan tanggal lahirnya
III. Negara dengan lagu kebangsaannya
Yang berkoresponden satu-satu adalah …
A. hanya II dan III
B. hanya I, II dan III
C. hanya I dan III
D. hanya I dan II
Jawaban : A
Pembahasan :
Yang berkoresponden satu-satu adalah …
I . Siswa dengan tempat duduknya
III. Negara dengan lagu kebangsaannya
17. Dari pernyataan berikut ini :
(i) Himpunan negara dan himpunan bendera
(ii) Semua penonton dan tiket masuk dalam pertandingan sepakbola
(iii) Semua siswa di kelasmu dan nama siswa pada daftar hadir di kelasmu
(iv) Semua siswa di sekolahmu dan guru-guru di sekolahmu
Yang berkoresponden satu-satu adalah …
A. (i), (iii), (iv)
B. (ii), (iii), (iv)
C. (i), (ii), (iii)
D. (i), (ii), (iv)
Jawaban : C
Pembahasan :
Yang berkoresponden satu-satu :
(i) Himpunan negara dan himpunan bendera
(ii) Semua penonton dan tiket masuk dalam pertandingan sepakbola
(iii) Semua siswa di kelasmu dan nama siswa pada daftar hadir di kelasmu
18. Dari pasangan himpunan-himpunan berikut ini.
(i) A = {x | 0 < x < 4, x bilangan cacah} dan B = {factor dari 4}
(ii) P = {huruf Vokal} dan Q = {bilangan asli kurang dari 4}
(iii) K = {a, b, c, d} dan L = {factor dari 6}
(iv) D = {1, 2, 3, 4} dan E = {bilangan prima kurang dari 8}
Yang berkoresponden satu-satu adalah …
A. (ii), (iii), (iv)
B. (i), (ii), (iv)
C. (i), (ii), (iv)
D. (i), (iii), (iv)
Jawaban : D
Pembahasan :
Yang berkoresponden satu-satu :
(i) A = {x | 0 < x < 4, x bilangan cacah} dan B = {factor dari 4}
(iii) K = {a, b, c, d} dan L = {factor dari 6}
(iv) D = {1, 2, 3, 4} dan E = {bilangan prima kurang dari 8}
19. Dari himpunan-himpunan berikut :
A = {x| x < 4, x bilangan Asli}
B = {x| x < 4, x bilangan Prima}
C = {x| x < 4, x factor prima dari 70}
D = {x| 2 < x < 10, x bilangan ganjil}
Yang berkoresponden satu-satu adalah …
A. A dan B
B. A dan C
C. B dan D
D. C dan D
Jawaban : B
Pembahasan :
Yang berkoresponden satu-satu :
A = {x| x < 4, x bilangan Asli}
C = {x| x < 4, x factor prima dari 70}
20. Dari himpunan pasangan berikut :
(i) {(a, 1), (b, 2), (c, 3), (d, 3)}
(ii) {(p, 5), (q, 7), (q, 9), (r, 11)}
(iii) {(s, 3), (t, 4), (u, 5), (v, 6)}
(iv) {(s, 3), (t, 4), (u, 3), (v, 6)}
Yang berkoresponden satu-satu adalah ..
A. (i)
B. (ii)
C. (iii)
D. (iv)
Jawaban : C
Pembahasan :
Yang berkoresponden satu-satu adalah ..
(iii) {(s, 3), (t, 4), (u, 5), (v, 6)}
Sudah selesai membaca dan berlatih Soal ini ? Ayo lihat dulu Soal Matematika lainnya