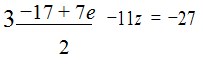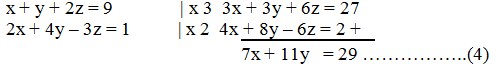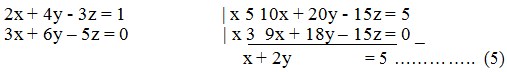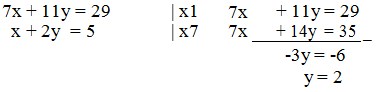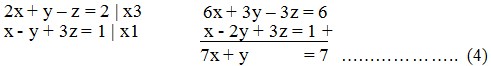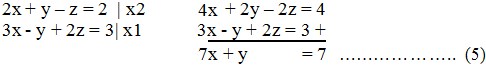Contoh Soal Sistem Persamaan Linear Dua Variabel (SPLDV) dan Persamaan Linear Tiga Variabel (SPLTV) dan Jawaban – Sistem Persamaan Linear Dua Variabel atau SPLDV adalah ada lebih dari satu persamaan linear dengan dua variabel yang hanya memiliki satu penyelesaian.

Sistem Persamaan linear tiga variabel (SPLTV) merupakan sebuah konsep dasar ilmu matematika yang sering digunakan untuk menyelesaikan persamaaan atau studi yang tidak dapat diselesaikan menggunakan persamaan linear satu variabel dan persamaan linear dua variabel (SPLDV).
Sistem Persamaan Linear Tiga Variabel (SPLTV) adalah kumpulan persamaan linear yang mempunyai solusi (atau tidak mempunyai solusi) yang sama untuk semua persamaan yang terdiri dari tiga variabel. Untuk menyelesaikan sistem persamaan linear tiga variabel ini, ada beberapa cara yaitu metode eliminasi, metode substitusi, dan metode gabungan (eliminasi dan substitusi).
Cara terbaik menyelesaikan SPLTV dengan metode Eliminasi-Substitusi (gabungan). Langkah-langkah menyelesaikan SPLTV dengan metode gabungan:
Eliminasi variabel pertama dengan memasang-masangkan dua persamaan dari ketiga persamaan sehingga diperoleh SPL baru yang sederhana.
Dari SPL baru, eliminasi lagi sehingga diperoleh nilai dari salah satu variabel yang ada.
Dari nilai variabel yang telah ada, substitusikan ke persamaan sebelumnya untuk memperoleh nilai variabel yang lainnya.
1 – 10 Soal SPLTV dan SPLDV Jawaban Beserta Pembahasan
Soal SPLDV (Sistem Persamaan Linear Dua Variabel)
1. Nilai p, yang memenuhi persamaan 4p + 3q = 20 dan 2p – q = 3 adalah…
A. 0
B. 1
C. 2
D. 3
Jawaban : C
Pembahasan :
4p + 3q = 20….(1)
2p – q = 3 ….(2)
Pilih salah satu persamaan misalnya persamaan (2), kemudian nyatakan salah satu variabelnya dalam bentuk variable yang lain.
2p – q = 3
-q = 3 – 2p
q = 2p + 3 …(3)
Substitusi persamaan(3) pada persamaan(1)
4p + 3q = 20
4p + 3(2p + 3) = 20
4p + 6p + 9 = 20
10p = 20
p = 2
2. Nilai x dan y berturut-turut yang memenuhi persaman x + 5y = 13 dan 2x – y = 4 adalah…
A. 2 dan 3
B. 3 dan 2
C. 4 dan 6
D. 1 dan 2
Jawaban : B
Pembahasan :
3. Himpunan penyelesaian dari sistem persamaan 2x + xy = 4 dan 3x + y =6 adalah:
A. {2,0}
B. {0,2}
C. { -2,0}
D. {0, -2}
Jawaban : A
Pembahasan :
4. Harga 8 buah buku tulis dan 6 buah pensil Rp. 14.400,00 harga 6 buah buku tulis dan 5 buah pensil Rp. 11.200,00. Jumlah harga 5 buah buku tulis dan 8 buah pensil adalah…
A. Rp. 13.600,00
B. Rp. 12.800,00
C. Rp. 12.400,00
D. Rp. 11.800,00
Jawaban : C
Pembahasan :
Model matematikanya adalah :
Misalkan :
buku tulis = x
Pensil = y
5. Penyelesaian dari sistem persamaan 3x + 5y = – 9 dan 5x + 7y = – 19 adalah x dan y. Nilai 4x + 3y adalah…
A. 41
B. 36
C. 23
D. 12
E. -23
Jawaban : E
Pembahasan :
Simak Juga : Contoh Soal Notasi Sigma
6. Umur Sani 7 tahun lebih tua dari umur Ari. Sedangkan jumlah umur mereka adalah 43 tahun. Berapakah umur masing-masing …
A. Sani 24 tahun dan Ari 19 tahun
B. Sani 25 tahun dan Ari 18 tahun
C. Sani 26 tahun dan Ari 17 tahun
D. Sani 27 tahun dan Ari 16 tahun
Jawaban : B
Pembahasan :
Misalkan :
Umur Sani = x tahun
Umur Ari = y tahun
x = 7 + y…(1)
x + y = 43 …(2)
7. Harga 2 kg salak dan 3 kg jeruk adalah RP.32.000,00, sedangkan harga 3 kg salak dan 2 kg jeruk adalah RP.33.000,00. Harga 1 kg salak dan 5 kg jeruk adalah…
A. Rp. 49.000,00
B. Rp. 41.000,00
C. Rp. 37.000,00
D. Rp. 30.000,00
Jawaban : C
Pembahasan :
Misalkan :
Harga 1 kg salak dilambangkan s
Harga I kg jeruk dilambangkan j
Diperoleh :
8. Berapakah nilai 6x – 2y jika x dan y merupakan penyelesaian dari system persamaan 3x + 3y = 3 dan 2x – 4y = 14 adalah…
A. 16
B. 12
C. 14
D. 18
Jawaban : C
Pembahasan :
9. Nilai x dan y yang memenuhi persamaan linier 2x + y = 6, dan 2x +4y = 9 adalah…
A. Y = -1 dan x = 2/5
B. Y = 1 dan x = 5/2
C. Y = -1 dan x = 3/5
D. Y = 1 dan x = 5/3
E. Y = 5/2 dan x = 1
Jawaban : B
Pembahasan :
Y = 1, dengan mensibstitusikan y = 1 pada persamaan 2x + y = 6, didapat x = 5/2 Jadi diperolehlah nilai y=1 dan x= 5/2.
10. Andi membeli 1 pulpen dan 1 buku dengan harga Rp 2000,- di toko yang sama Budi membeli 5 pulpen dan 2 buku dengan harga Rp 7000,- . berapakah harga 1 buah pilpen?
A. Rp 1000,-
B. Rp 1500,-
C. Rp 850,-
D. Rp 500,-
E. Rp 1200,-
Jawaban : A
Pembahasan :
Misal x = pulpen dan y= buku
Maka diperoleh persamaan x + y = 2000, dan 5x +2y = 7000. Sehingga:
11 – 20 Contoh Soal Sistem Persamaan Linear Dua Variabel (SPLDV) dan Jawaban
11. Ibu membeli 3 ember dan I panci dengan harga Rp 50.000,-. Di toko yang sama Ani membeli 1 ember dan 2 panci dengan harga Rp 65.000,-. Berapakah harga untuk 1 ember dan 1 panci ?
A. Rp 25.000,-
B. Rp 30.000,-
C. Rp 32.000,-
D. Rp 36.000,-
E. Rp 40.000,-
Jawaban : D
Pembahasan :
Misal x = ember, dan y = panic
Maka diperoleh persamaan 3x + y = 50000, dan x + 2y = 65000. Sehingga:
Dengan mensubstitusikan x = 7000 kepersamaan 3x + y = 50000, mak diperoleh y = 29000.
Sehingga harga untuk 1 ember dan 1 panci adalah x +y = 7000 + 29000 = Rp 36000,-
12. Nilai x dan y yang memenuhi dari persamaan linier 2x + 3y = 12 dan x + 6y = 9 adalah…
A. X = 5 , y = 2/3
B. X = 3 , y = 2/3
C. X = 2/5, y = 5
D. X = 2/3, y = 5
E. X = 5, y = 2/5
Jawaban : D
Pembahasan :
13. Harga 1 buku dan 1 pulpen Rp 3.000,-. Jika harga 2 buku dan 3 pulpen Rp 7.000,-. Maka harga 5 pulpen dan 4 buku adalah …
A. Rp 15.000,-
B. Rp 14.500,-
C. Rp 14.000,-
D. Rp 13.500,-
E. Rp 13.000,-
Jawaban : E
Pembahasan :
Misal x = buku dan y= pulpen, sehingga diperoleh persamaan
Dengan mensubstitusikan y = 1000 ke persamaan x + y = 3000, di peroleh x = 2000.
Jadi harga untuk 5 pupen dan 4 buku adalah 5(1000) + 4 (2000) = 5000+8000 = Rp 13000,-
14. Nilai x dan y yang memenuhi persamaan linier 3x + 2y + 6 = -1, dan 2x + 3y + 3 = 9 adalah …
A. X = 33/5 , y = -32/5
B. X = -33/5 , y = -32/5
C. X = -33/5 , y = 32/5
D. X = 32/5, y = -33/5
E. X = -32/5 , y = 33/5
Jawaban : C
Pembahasan :
Dengan mensibstitusikan y= 32/5 ke dalam persamaan 2x +3y+3=9 di perolehlah x= -33/5
15. Abdul membeli 2 kg jeruk dan 3kg apel seharga Rp 80.000,-. Di toko yang sama Dani membeli 1 kg jeruk dan 2 kg apel dengan harga Rp 50.000,-. Maka harga 10 kg apel adalah. . .
A. Rp 250.000,-
B. Rp 200.000,-
C. Rp 150.000,-
D. Rp 100.000,-
E. Rp 120.000
Jawaban : B
Pembahasan :
Lihat Juga : Soal Kesebangunan dan Kekongruenan
16. Sopyan membeli 5 pulpen dan 3 buku seharga Rp 12.000,-, di toko yang sama heri membeli 5 pulpen dan 2 buku seharga Rp 10.000,-. Berapakah harga 1 buku dan 1 pulpen?
A. Rp 3.200,-
B. Rp 4.200,-
C. Rp 4.000,-
D. Rp 3.000,-
E. Rp 2.500,-
Jawaban : A
Pembahasan :
Misal pulpen = x dan buku = y, sehingga:
Dengan mensibstitusikan y = 2000 ke persamaan 5x + 3y = 12000, diperoleh x = 1200.
Sehingga harga untuk 1 pulpen dan 1 buku = 2000 + 1200 = Rp 3.200,-
17. Nilai x dan y yang memenuhi dari persamaan linier 8x + 2y = 16, dan 4x + 2y = 8 adalah…
A. x= -2 , y = -2
B. x = 0, y = 2
C. x = 2 , y = 0
D. x = 0 , y = -2
E. x = 2 , y= 2
Jawaban : C
Pembahasan :
8x + 2y = 16
4x + 2y = 8
4x = 8
x = 2
Dengan mensubstitusikan x=2 ke persamaan 4x + 2y = 8 di dapatkan y= 0.
18. Nilai x dan y yang memenuhi dari persamaan linier 5x + 6y – 20 = 10 , dan 6x + 10y – 30 =50 adalah…
A. x= -250/7 , y = -160/7
B. x = 350, y = -160/7
C. x = 160/7 , y = -250/7
D. x = -250 , y = 160/7
E. x = -350/7 , y= -160/7
Jawaban : D
Pembahasan :
Dengan mensubstitusikan y= 160/7 kepersamaan 5x + 6y = 30, sehingga diperoleh x= -250/7
19. Himpunan penyelesaian dari sistem persamaan 12x + 6y=6 dan 4x + y = -3, adalah . . .
A. {(5 , 2)}
B. {(2 , -5)}
C. {(5 , -2)}
D. {(-2 , 5)}
E. {(-5 , 2)}
Jawaban : D
Pembahasan :
12x + 6y = 6…………..(i)
4x + y = -3…………….(ii)
Kita eliminasi kedua persaman tersebut dengan menyamakan nilai x nya, persamaan (i) dikali 1 , sedangakan persamaan (ii) dikali 3, maka nilainya:
12x + 6y = 6
12x + 3y = -9
Setelah dieliminasi didapat nilai y = 5 dan nilai x = -2.
Jadi, himpinan penyelesaiannya {(-2,5)}
20. Akar-akar dari sistem persamaan 2x – y = 8 dan x + 3y = -10, adalah . . .
A. x = 2 dan y = 4
B. x = 2 dan y = -4
C. x = -2 dan y = 4
D. x = -2 dan y = -4
Jawaban : B
Pembahasan :
Kita eliminasi kedua persaman tersebut dengan menyamakan nilai x nya, persamaan (i) dikali 1 , sedangkan persamaan (ii) dikali 2, maka nilainya:
2x – y = 6
2x + 6y = -20
Setelah dieliminasi didapat nilai y = -4 dan nilai x = 2.
Jadi, akar-akar dari sistem persamaannya adalah x = 2 dan y = -4
21 – 30 Soal SPLTV dan SPLDV Jawaban
21. Penyelesaian dari sistem persamaan 3a + 5b = 21 dan 2a – 7b = 45 adalah (a,b), yaitu . . .
A. (-3,12)
B. (-3,-12)
C. (12,-3)
D. (-12,-3)
Jawaban : C
Pembahasan :
3a + 5b = 21……………….(i)
2a – 7b = 45………………….(ii)
Kita eliminasi kedua persaman tersebut dengan menyamakan nilai a nya, persamaan (i) dikali 2 , sedangakan persamaan (ii) dikali 3, maka nilainya:
6a + 10b = 42
6a – 21b = 135
Setelah dieliminasi didapat nilai b = -3 dan nilai a = 12.
Jadi, penyelesaian dari sistem persamaannya adalah a = 12 dan b = -3
22. {(m,n)} adalah himpunan penyelesaian dari system persamaan 2m – 3n = 2 dan 5m + 2n = 24. maka nilai (m-n) adalah. . .
A. 6
B. 4
C. 2
D. -6
Jawaban : C
Pembahasan :
2m – 3n = 2……………….(i)
5m + 2n = 24………………….(ii)
Kita eliminasi kedua persaman tersebut dengan menyamakan nilai m nya, persamaan (i) dikali 5, sedangkan persamaan (ii) dikali 2, maka nilainya:
10m – 15n = 10
10m + 4n = 48
Setelah dieliminasi didapat nilai n = 2 dan nilai m = 4.
Jadi, nilai dari (m – n) adalah..( 4 – 2) = 2
23. Harga 4 buah buku dan 3 batang pensil adalah Rp 2.500,00, sedangkan 2 buku dan 7 batang pensil adalah Rp 2.900,00. Harga 2 lusin buku dan 4 lusin pensil adalah. . .
A. Rp 23.500,00
B. Rp 24.000,00
C. Rp 27.000,00
D. Rp 29.500,00
Jawaban : B
Pembahasan :
Kita misalkan : buku = x ; pensil = y
Yang ditanyakan : 2 lusin buku dan 4 lusin pensil, adalah?
Jawab :
Didapat persamaan linier dua variabelnya :
4x + 3y = 2.500
2x + 7y = 2.900
Kita eliminasi kedua persaman tersebut dengan menyamakan nilai x nya, persamaan (i) dikali 1 , sedangkan persamaan (ii) dikali 2, maka nilainya:
4x + 3y = 2.500
4x + 14y = 5.800
Setelah dieliminasi didapat nilai y = 300 dan nilai x = 400.
Didapat harga 1 buah buku tulis Rp 400,00 , sedangakan harga 1 buah pensil Rp 300,00
Jadi, Harga 2 lusin buku dan 4 lusin pensil adalah:
= 2(12). Rp 400,00 + 4(12). Rp 300,00
= 24. Rp 400,00 + 48. Rp 300,00
= Rp 9.600,00 + Rp 14.400,00
= Rp 24.000,00
24. Dua buah bilangan, tiga kali bilangan pertama ditambah lima kali bilangan kedua sama dengan -1, sedangkan lima kali bilangan pertama dikurangi enam kali bilangan kedua sama dengan -16. maka sistem persamaan linier dua variabelnya adalah . . .
A. 3p + 5q = -1 dan 5p – 6q = -16
B. 3p – 5q = -1 dan 5p + 6q = -16
C. 3p + 5q = 1 dan 5p – 6q = 16
D. 3p + 5q = -1 dan 5p + 6q = 16
Jawaban : A
Pembahasan :
Bila p adalah bilangan pertama, dan q adalah bilangan kedua, maka sistem persamaan linier dua variabel dari permasalahan diatas adalah : 3p + 5q = -1 dan 5p – 6q = -16
25. . Koordinat titik potong antara garis 2x – y = 0 dan garis x + y +6 = 0, adalah . . .
A. (2,-4)
B. (-2,-4)
C. (2,4)
D. (4,-2)
Jawaban : C
Pembahasan :
2x – y = 2………………..(i)
x + y = -6………………….(ii)
Kita eliminasi kedua persaman tersebut dengan menyamakan nilai x nya, persamaan (i) dan persamaan (ii) kita eliminasi didapat nilai y = 4 dan nilai x = 2.
Jadi, koordinat titik potongnya adalah (2,4)
Simak Juga : Soal Induksi Matematika
26. Harga 8 buku tulis dan 6 buah pena adalah Rp 14.400,00, sedangkan harga 6 buah buku tulis dan 5 buah pena adalah Rp 11.200,00, maka harga sebuah buku dan harga sebuah pena, adalah. . .
A. Buku = Rp 1.200,00 dan Pensil = Rp 800,00
B. Buku = Rp 800,00 dan Pensil = Rp 1.200,00
C. Buku = Rp 1.000,00 dan Pensil = Rp 800,00
D. Buku = Rp 800,00 dan Pensil = Rp 1.000,00
Jawaban : A
Pembahasan :
Kita misalkan : buku = x ; pensil = y
Yang ditanyakan : harga sebuah buku dan harga sebuah pensil, adalah?
Jawab :
Didapat persamaan linier dua variabelnya ;
8x + 6y = 14.400
6x + 5y = 11.200
Kita eliminasi kedua persaman tersebut dengan menyamakan nilai x nya, persamaan (i) dikali 3 , sedangkan persamaan (ii) dikali 4, maka nilainya:
24x + 18y = 43.200
24x + 20y = 44.800
Setelah dieliminasi didapat nilai y = 800 dan nilai x = 1.200.
Didapat harga 1 buah buku tulis Rp 1.200,00 , sedangakan harga 1 buah pensil Rp 800,00
27. Jumlah dua bilangan adalah 67 dan selisihnya 13. Jika dibuat suatu pecahan dengan pembilangnya bilangan yang kecil, maka penyebut pecahan tersebut adalah . . .
A. 67
B. 40
C. 27
D. 13
Jawaban : B
Pembahasan :
Bila a adalah bilangan pertama, dan b adalah bilangan kedua, maka sistem persamaan linier dua variabel dari permasalahan diatas adalah :
a + b = 67 …………………(i)
a – b = 13………………….(ii)
Kita eliminasi kedua persaman tersebut dengan menyamakan nilai a nya, persamaan (i) dan persamaan (ii) kita eliminasi didapat nilai a = 40 dan nilai b = 27. jika dibuat pecahan dengan pembilang yang lebih kecil maka nilai pembilangnya 27, sedangkan nilai dari penyebutnya adalah 40.
Jadi, nilai penyebutnya adalah 40
28. Penyelesaian dari system persamaan linear 2p + 3q – 12 = 0 dan 4p – 7q + 2 = 0, adalah (p,q), maka nilai dari p + q adalah . . .
A. 5
B. 3
C. -3
D. -5
Jawaban : A
Pembahasan :
2p + 3q = 12……………….(i)
4p – 7q = -2….……………….(ii)
Kita eliminasi kedua persaman tersebut dengan menyamakan nilai p nya, persamaan (i) dikali 2, sedangkan persamaan (ii) dikali 1, maka nilainya:
4p + 6q = 24
4p – 7q = -2
Setelah dieliminasi didapat nilai q = 2 dan nilai p = 3.
Jadi, nilai dari p + q adalah = 3 + 2 = 5
29. Himpunan penyelesaian dari SPLDV berikut adalah …
x + 5y = 13
2x – y = 4
A. {(3,2)}
B. {(1,2)}
C. {(2,3)}
D. {(1,-2)}
Jawaban : A
Pembahasan :
Dari uraian diperoleh nilai x = 3 dan y = 2. Jadi dapat dituliskan Hp = {(3,2)}.
30. Himpunan penyelesaian dari SPLDV berikut adalah …
x + y = 3
2x – 2y = 10
A. {(4,-1)}
B. {(1,4)}
C. {(1,-4)}
D. {(2,-4)}
Jawaban : C
Pembahasan :
Dari uraian diperoleh nilai x = 1 dan y = -4. Jadi dapat dituliskan Hp = {(1,-4)}
Soal Esai
31. Ikhsan dan Jono pergi ke toko buah bersama-sama membeli apel dan mangga. Ikhsan membeli 2 kg apel dan 5 kg mangga dengan hargaRp29.500. Jono membeli 4 kg apel dan 3 kg mangga dengan harga Rp34.500. Berapakah harga 1 kg apel dan 1 kg mangga?
Jawaban :
Pembahasan :
Diketahui:
Ikhsan membeli 2 kg apel dan 5 kg mangga seharga Rp29.500
Jono membeli 4 kg apel dan 3 kg mangga seharga Rp34.500
Dit: dengan metode eliminasi tentukan harga 1 kg apel dan 1 kg mangga?
Jawab:
Misal: x = harga 1 kg apel
y = harga 1 kg mangga
Dari permasalahan diatas diperoleh pers:
2x + 5y = 29.500
4x + 3y = 34.500
Akan ditentukan nilai x dan y yang merupakan penyelesaian sistem persamaan linear tersebut.
eliminasi variabel y untuk mencari nilai x:
32. Mesin produksi A menghasilkan 100 unit barang per jam, sedangkan mesin produksi B menghasilkan 150 unit barang per jam kedua mesin itu diharapkan dapat menghasilkan 2.600 unit barang. Jumlah jam kerja dalam satu hari untuk mesin A dan mesin B adalah 20 jam. Berapa jam mesin A dan mesin B harus bekarja dalam satu hari?
Jawaban :
Pembahasan :
Diketahui :
Mesin A menghasilkan 100 unit barang per jam Mesin B menghasilkan 150 unit barang per jam
kedua mesin itu diharapkan dapat menghasilkan 2.600 unit barang
Jumlah jam kerja dalam satu hari untuk mesin A dan mesin B adalah 20 jam
Dit: berapa jam mesin A dan B harus bekerja dalam satu hari (metode subtitusi)?
Jawab:
Misal:
x = jumlah jam kerja satu hari mesin produksi A bekerja y = jumlah jam kerja satu hari mesin produksi B bekerja Dari permasalahan diatas diperoleh pers:
100x + 150y = 2.600
x + y = 20
Akan ditentukan nilai x dan y yang merupakan penyelesaian sistem persamaan linear tersebut.
Dari persamaan (2) diperoleh:
x + y = 2.000
x = 20 − y
Sub x = 20 − y ke pers (1):
100x + 150y = 2.600
100(20 − y) + 150y = 2.600
2.000 − 100y + 150y = 2.600
50y = 2.600 − 2.000
50y = 600
y = 12
Sub y = 12 ke pers (2):
x + y = 20
x + 12 = 20
x = 20 − 12
x = 8
HP= {8; 12}
x = 8 dan y = 12 disubtitusikan ke pers (1) dan (2):
100x + 150y = 100(8) + 150(12)
= 800 + 1800 = 2600 (benar)
x + y = 8 + 12 = 20 (benar)
Jadi, mesin A bekerja 8 jam perhari dan mesin B bekerja 20 jam perhari
33. Diketahui dua bilangan x dan y. Jumlah dari tiga kali bilangan pertama dengan empat kali bilangan kedua sama dengan 66. Selisih dari empat kali bilangan pertama dengan tiga kali bilangan kedua sama dengan 13. Carilah bilangan- bilangan itu?
Selesaikan permasalahan SPLDV diatas dengan menggunakan metode eliminasi!
Jawaban :
Pembahasan :
Diketahui:
Dua bilangan x dan y
Jumlah 3 kali bilangan pertama dengan 4 kali bilangan kedua sama dengan 66
Selisih dari 4 kali bilangan pertama dengan 3 kali bilangan kedua sama dengan 13
Ditanyakan: Tentukan ke dua bilangan tersebut? Jawab:
Untuk membuat model matematika dari permasalahan diatas maka kita misalkan:
x = bilangan pertama
y = bilangan kedua
Dari permasalahan diatas diperoleh persamaan:
3x + 4y = 66 . . . (1)
4x − 3y = 13. . . (2)
Persamaan (1) dan (2) membentuk sistem pesamaan linear dua peubah, yaitu:
3x + 4y = 66
4x − 3y = 13
Akan ditentukan nilai x dan y yang merupakan penyelesaian sistem persamaan linear tersebut.
Untuk mencari nilai x, kita eliminasi variabel y diperoleh:
34. Jika uang Rp 140.000 diberikan kepada 3 orang tukang kebun dan seorang pembersih ruangan dan Rp 220.000 diberikan kepada 4 orang tukang kebun dan 2 orang pembersih ruangan, maka tentukanlah besarnya uang yang diterima oleh masing-masing tukang kebun dan tenaga pembersih ruangan!
Selesaikan permasalahan SPLDV diatas dengan menggunakan metode substitusi !
Jawaban :
Pembahasan :
Diketahui:
Uang 3 tukang kebun dan 1 pembersih ruangan adalah Rp 220.000 Uang 4 tukang kebun dan 2 pembersih ruangan adalah Rp 220.000 Ditanyakan:
Berapakah uang yang diterima tukang kebun dan tenaga pembersih? Jawab:
Misalkan: x = uang tukang kebun
y = uang tenaga pembersih ruangan Dari permasalahan diatas diperoleh persamaan:
3x + y = 140.000 . . . (1)
4x + 2y = 220.000. . . (2)
Persamaan (1) dan (2) membentuk sistem pesamaan linear dua peubah, yaitu:
3x + y = 140.000
4x + 2y = 220.000
Akan ditentukan nilai x dan y yang merupakan penyelesaian sistem persamaan linear tersebut.
Dari persamaan (1) diperoleh:
3x + y = 140.000
⇔ y = 140.000 − 3x
Subtitusikany = 140.000 − 3x ke persamaan (2) diperoleh:
4x + 2y = 220.000
4x + 2(140.000 − 3x) = 220.000
4x + 280.000 − 6x = 220.000
−2x = 220.000 − 280.000
−2x = −60.000
x = 30.000
Subtitusikan x = 30.000 ke persamaan (1) diperoleh: 3x + y = 140.000
3(30.000) + y = 140.000
90.000 + y = 140.000
y = 140.000 − 90.000
y = 50.000
HP= {30.000; 50.000}
x = 30.000 dan y = 50.000 masing-masing disubtitusikan ke persamaan (1) dan (2) diperoleh:
4x + 2y = 4(30.000) + 2(50.000)
= 120.000 + 100.000
= 220.000 (benar)
3x + y = 3(30.000) + 50.000
= 90.000 + 50.000
=140.000 (benar)
Jadi, uang yang diterima tukang kebun adalah Rp 30.000, dan uang yang diterima tenaga pembersih ruangan adalah Rp 50.000.
35. Perhatikan permasalahan dibawah ini!
Masalah 1 :
Sore ini Rudi pergi ke toko alat tulis dan membeli 5 buah pena dan 2 buah pensil. Ketika Dewi pulang sekolah, Dewi mampir ke toko alat tulis dan membeli 3 buah pena dan 2 buah pensil. Berapa jumlah pena dan pensil yang ada?
Masalah 2 :
Dua anak berbelanja disebuah toko. Anak pertama membayar Rp 7.450 untuk membeli 3 susu kotak dan 2 bungkus keripik, sedangkan anak kedua harus membayar Rp 11.550 untuk membeli 5 susu kotak dan 3 bungkus keripik. Berapakah harga 1 buah susu kotak dan harga 1 bungkus keripik? Tentukanlah mana masalah yang termasuk dalam SPLDV? Lengkapi dengan alasanmu!
Jawaban :
Pembahasan :
Diketahui:
Masalah 1: Rudi pergi ke toko alat tulis dan membeli 5 buah pena dan 2 buah pensil .
Dewi mampir ke toko alat tulis dan membeli 3 buah pena dan 2 buah pensil.
Masalah 2: Anak pertama membayar Rp 7.450 untuk membeli 3 susu kotak dan 2 bungkus keripik
Anak kedua harus membayar Rp 11.550 untuk membeli 5 susu kotak dan 3 bungkus keripik
Ditanya : Manakah masalah yang merupakan SPLDV? Berikan alasannya!
Jawab :
Dari masalah 1:
Untuk membuat model matematika dari permasalahan diatas maka kita misalkan:
x ∶ banyaknya pena
y ∶ banyaknya pensil
Dari permasalahan yang diketahui maka diperoleh model matematikanya :
5x + 2y
3x + 2y
Dari masalah 2:
Untuk membuat model matematika dari permasalahan diatas maka kita misalkan:
x ∶ banyaknya susu kotak
y ∶ banyaknya keripik
Dari permasalahan yang diketahui maka diperoleh model matematikanya:
3x + 2y =7450
5x + 3y =1155
Dari 2 masalah yang ada, model matematika yang kita peroleh yaitu: Masalah 1:
5x + 2y
3x + 2y
Masalah 2 :
3x + 2y =7450
5x + 3y =1155
Dapat dilihat bahwa yang model matematika yang sesuai dengan bentuk umum SPLDV yaitu Masalah 2.
Bentuk umum SPLDV adalah:
a1x + b1y = c1 a2x + b2y = c2
Sesuai dengan model matematika dari Masalah 2:
3x + 2y =7450
5x + 3y =1155
Jadi yang merupakan masalah SPLDV adalah Masalah 2.
Soal SPLTV (Sistem Persamaan Linear Tiga Variabel)
1. Tentukan penyelesaian SPLTV berikut dengan substitusi :
x + y + 2x = 9 ……….. (1)
2x + 4y – 3z = 1 …….. (2)
3x + 6y – 5z = 0 …….. (3)
Jawaban :
Dari persamaan (1), kita dapatkan x = 9 – y – 2z ……….. (4)
Persamaan (4) disubstitusikan ke persamaan (2) dan (3)
2(9 – y – 2z) + 4y – 3z = 1
2y – 7 z = -17 ………………………………………………. (5) dan
3(9 – y – 2z) + 6 – 5z = 0
3y – 11z = -27 ……………………………………………….(6)
Sehingga diperoleh SPLTV berikut ini :
2y – 7z = -17 …………………………………………………(5)
3y – 11z = -27 ………………………………………………..(6)
Selanjutnya, kita dapat mencari nilai y dan z dengan cara substitusi seperti pada SPLDV.
Dari persamaan (5) diperoleh: y =
…………………. (7)
Substitusi persamaan (7) ke persamaan (6)
-51 + 21z – 22z = 54
-z = -3
z = 3
Kemudian nilai z = 3 disubstitusikan ke persamaan (7), diperoleh nilai y = 2
Substitusikan y = 2 dan z=3 ke persamaan (4) diperoleh nilai x= 1.
Jadi SPLTV tersebut mempunyai penyelesaian tunggal yaitu (1,2,3) atau Himpunan Penyelesaiannya adalah {(1,2,3)}.
2. Tentukan penyelesaian dari SPLTV dengan substitusi :
2x + y – z = 2 ………… (1)
x – 2y + 3z = 1 ……….. (2)
3x – y + 2z = 3 ……….. (3)
Jawaban :
Misalkan substitusi dimulai pada variabel z terlebih dahulu (persamaan yang paling sederhana).
Dari persamaan (1) diperoleh: z = 2x + y – 2 …………….. (4)
Persamaan (4) disubstitusikan ke persamaan (2) dan (3) diperoleh:
x – 2y + 3(2x + y – 2) = 1
7x + y = 7 ………………………………………………….. (5)
dan
3x – y + 2(2x + y – 2) = 3
7x + y = 7 …………………………………………………. (6)
Persamaan (5) sama dengan persamaan (6), sehingga dari kedua persamaan ini dapat kita peroleh nilai satu peubah sebagai fungsi dari peubah yang lain,
misalnya:
y = 7 – 7x ………………………………………………………. (7)
Substitusikan persamaan (7) ke persamaan (4), maka diperoleh: z = 2x + (7 – 7x) – 2
z = -5x + 5
Jadi, penyelesaian dari SPLTV tersebut adalah:
x = x
y = 7 – 7x
z = 5 – 5x
Penyelesaian dari SPLTV ini banyak sekali, tergantung pada nilai x yang kita tentukan, misalnya.
Jika x = 1, maka y = 0 dan z = 0 atau Jika x = 0, maka y = 7 dan z = 5 atau
Jika x = -1, maka y = 14 dan z = 10 dan seterusnya
Dengan kata lain SPLTV ini mempunyai tak hingga banyak anggota dalam Himpunan Penyelesaiannya.
3. Tentukan penyelesaian dari SPLTV dengan substitusi
x + 2y – 3z = -1 …………………………………………………. (1)
3x – y + 2z = 7 …………………………………………………… (2)
5x + 3y – 4z = 2 …………………………………………………. (3)
Jawaban :
Misalkan substitusi dimulai pada variabel x, dari persamaan (1) diperoleh: x = -2y + 3z – 1……………………………………………….. (4)
Persamaan (4) disubstitusikan ke persamaan (2) dan (3) diperoleh: 3(-2y + 3z – 1) – y + 2z = 7
-7y + 11z = 10 …………………………………………….. (5) dan
5(-2y + 3z – 1) + 3y – 4z = 2
-7y + 11z = 7 ………………………………………………. (6)
Persamaan (5) dan (6) menyatakan bahwa SPLDV tersebut tidak konsisten sehingga SPLTV tidak mempunyai penyelesaian.
4. Tentukan penyelesaian dari SPLTV berikut dengan Eliminasi:
x + y + 2z = 9 ………………. (1)
2x + 4y – 3z = 1 ……………. (2)
3x + 6y – 5z = 0 ……………. (3)
Jawaban :
Eliminasi z dari persamaan (1) dan (2) sehingga diperoleh:
Eliminasi z dari persamaan (2) dan (3) sehingga diperoleh persamaan:
Dari persamaan (4) dan (5) diperoleh SPLDV, yaitu:
7x + 11y = 29 …………… (4)
x + 2y = 5 …………….. (5)
Eliminasi x pada persamaan (4) dan (5) diperoleh nilai y :
Substitusikan nilai x = 1 dan y = 2 ke persamaan yang paling sederhana (misal persamaan (1)) sehingga diperoleh nilai z
x + y + 2x = 9
1 + 1 + 2z = 9
2z = 6
z = 3
Penyelesaian SPLTV tersebut adalah x = 1, y = 2, z = 3 atau (1, 2, 3)
Sedangkan himpunan penyelesaiannya {(1,2,3)}
5. Tentukan penyelesaian dari SPLTV berikut dengan Eliminasi
2x + y – z = 2 ……………… (1)
x – 2y + 3x = 1 ……………. (2)
3x – y + 2z = 3 …………….. (3)
Jawaban :
Eliminasi z dari persamaan (1) dan (2) diperoleh persamaan (4)
Eliminasi z dari persamaan (1) dan (3) diperoleh persamaan (5)
Terlihat bahwa persamaan (4) sama dengan persamaan (5) sehingga kita peroleh nilai satu variabel yang merupakan fungsi dari variabel yang lain, yaitu y = 7 – 7x.
Substitusikan nilai y = 7 – 7x ke persamaan (1), diperoleh:
2x + (7 – 7x) – z = 2
z = -5x + 5
Penyelesaian SPLTV tersebut adalah:
x = x
y = -7x + 7
z = -5x + 5
Dengan kata lain, SPLTV ini mempunyai banyak penyelesaian tergantung pada nilai variabel x yang kita tentukan.
Sudah selesai membaca dan berlatih soal spltv dan spltv ini ? Ayo lihat dulu Soal Matematika lainnya




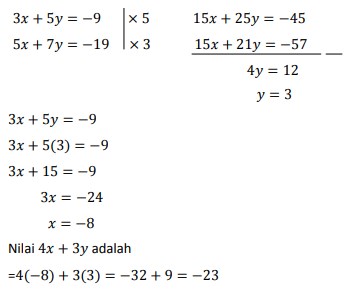


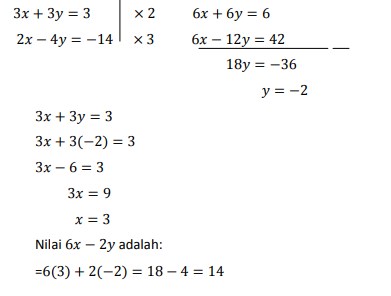
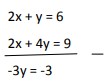
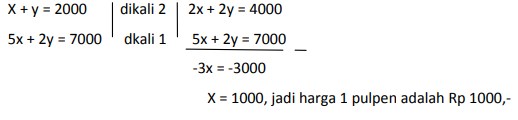
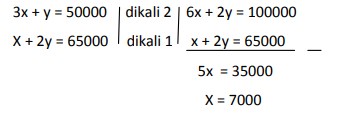
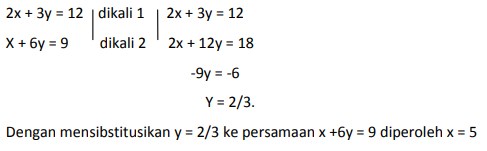
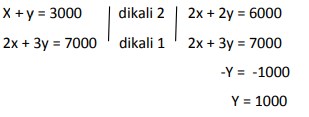
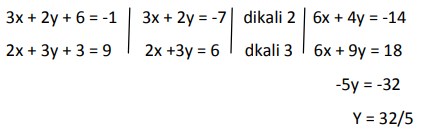

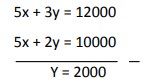
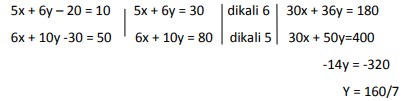
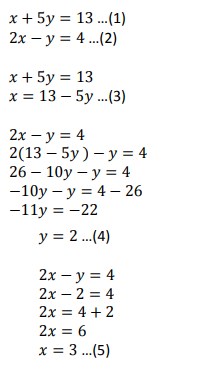
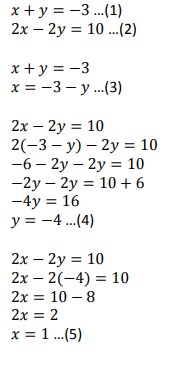


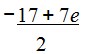 …………………. (7)
…………………. (7)