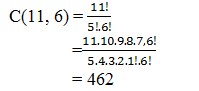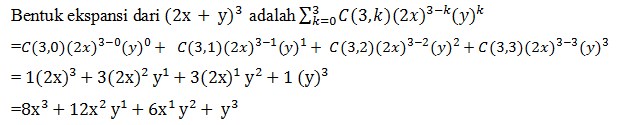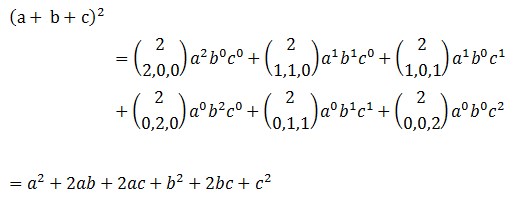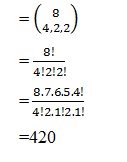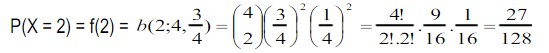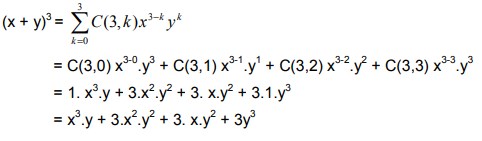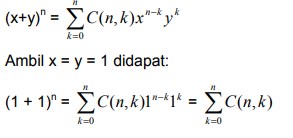Contoh Soal Teorema Binomial Pilihan Ganda dan Kunci Jawaban beserta Pembahasan – Dalam matamatika bidang aljabar elementer, teorema binomial adalah rumus penting yang memberikan ekspansi pangkat dari penjumlahan antara dua variabel. Versi yang paling sederhana menyambat bahwa:
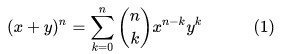

Gagasan setiap bilangan riil atau kompleks x dan y, serta bilangan bulat tak negatif n. Koefisien binomial yang muncul dalam persamaan (1) kawa didefinisikan dalam bentuk fungsi faktorial n!:
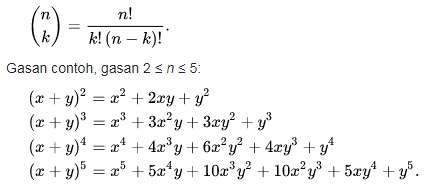
Lihati bahwa:
- Pangkat dari x bagarak turun dimana pada suku nang pertama dimulai lawan n x^{n} wan pada suku terakhir sama dengan 0 (x^0=1).
- Gasan pangkat dari y berlaku sebaliknya dimana pada suku pertama sama dengan 0 (y^0=1) wan pada suku terakhir sama dengan n (y^n).
1 – 10 Contoh Soal Teorema Binomial dan Pembahasan
1. Tentukan koefisien dari a5b6 dalam penjabaran (a + b) 11 :
A. 462
B. 426
C. 624
D. 246
E. 240
Jawaban : A
Pembahasan :
2. Tentukan koefisien dari x2y3 dalam ekspansi (x + 3y)5 !
A. 20 x2y3
B. 45 x2y3
C. 90 x2y3
D. 180 x2y3
E. 200 x2y3
Jawaban : C
Pembahasan :
3. Ekspansikan (2x + y)3
A. 8x3+((12x)2 y)1+ ((6x)1 y)2+(y)3
B. 4x3+((12x)2 y)1+ ((6x)1 y)2+(y)3
C. 2x3+((12x)2 y)1+ ((6x)1 y)2+(y)3
D. 4x3+((12x)2 y)1+ ((2x)1 y)2+(y)3
E. 8x3+((12x)2 y)1+ ((2x)1 y)2+(y)3
Jawaban : A
Pembahasan :
4. Ekspansikan (a + b + c)2
A. a2+2ab+2ac+b2+2bc+c2
B. a2+2ab+2ac+b2+2bc+c4
C. a2+2ab+2ac+b+2bc+c2
D. a2+2ab+2ac+b2+2bc+c
E. a2+2ab+2ac+b2+2bc+c
Jawaban : A
Pembahasan :
5. Dalam ekspresi (x + y + z)8 , koefisien dari x4y2z2 adalah
A. 400
B. 410
C. 420
D. 430
E. 450
Jawaban : C
Pembahasan :
Simak Juga : Soal Ujian Matematika Kelas 11 Semester 1 dan Kunci Jawaban
6. Probabilitas bahwa sejenis komponen tertentu yang akan bertahan terhadap sebuah uji kejut adalah ¾.Carilah probabilitas dimana 2 dari 4 komponen yang selanjutnya diuji akan bertahan.
Jawaban :
Pembahasan :
Diketahui x = 2; n = 4 ; p : ¾ maka :
7. Jabarkan bentuk (x + y)³ adalah. . .
Jawaban :
Pembahasan :
8. Tentukan suku keempat dari (x – y)5 adalah. . .
Jawaban :
Pembahasan :
Suku ke-4, maka k = 3 sehingga suku ke – 4 adalah : C(5,3).x5-3.(-y)3 = -10x2y3
9. Tunjukan bahwa
Jawaban :
Pembahasan :
10. Berapa banyak solusi dari persamaan: a + b = 13, 3 ≤ a ≤8, 6 ≤ b ≤ 9 dengan a dan b bilangan bulat.
Jawaban :
Pembahasan :
Dengan menggunakan fungsi pembangkit maka masalah diatas analog dengan mencari koefisien pangkat 13 dari: