Soal PAS Matematika Kelas 12 Semester 1 Kurikulum 2013 [Update]

Penilaian matematika baik itu Penilaian Akhir Semester sebenarnya ditujukan untuk menilai siswa dalam matematika, baik itu kelemahan dalam menghitung, sebenarnya untuk membantu siswa mengatasi kelemahan tersebut untuk mengubahnya menjadi kekuatan. Siswa diharapkan akan menemukan makna dan kepercayaan diri dalam memiliki tujuan pembelajaran yang konkret, karena penilaian ini memberi mereka panduan tentang apa yang harus mereka pelajari dan tingkatkan.

Meskipun dapat memunculkan perasaan gugup dan cemas saat ujian, penilaian matematika tidak digunakan untuk mengintimidasi siswa namun ada untuk membantu siswa lebih dekat dengan keunggulan matematika. Tanpa adanya ujian, kita tidak tahu bagaimana seseorang dapat benar-benar mengetahui apakah keterampilan matematika mereka meningkat? Bagaimana kita bisa tahu jika siswa secara efektif menyerap materi yang diajarkan? maka sebagai seorang siswa anda tidak perlu membenci ujian, bukakah lebih baik anda bersemangat dalam menghadapi ujian.

Topik matematika kelas 12 semester 1 :

• Limit Fungsi
• Turunan Fungsi Trigonometri
• Statistika

1 – 10 Contoh Soal PAS Matematika Kelas 12 dan Jawaban

1. Nilai dari 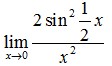adalah …

A. 0 

B. ½

C. 1 

D. 2

E. ∞

Jawaban : B

Pembahasan : 

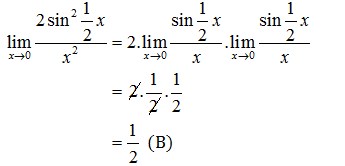
2. Nilai dari 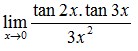 adalah …

A. 0 

B. 3/2

C. 2/3

D. 2

E. 6

Jawaban : D

Pembahasan :

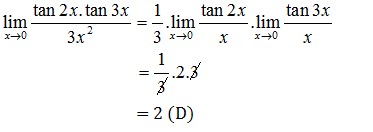
3. Nilai dari 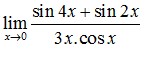adalah …

A. ¼

B. ½

C. 1

D. 3/2

E. 2

Jawaban : E

Pembahasan :

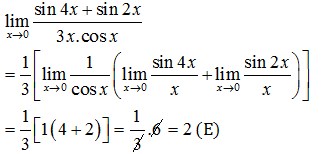
4. Nilai dari 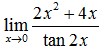   adalah …

A. 0 

B. 1

C. 2 

D. 3

E. 4

Jawaban : C

Pembahasan :

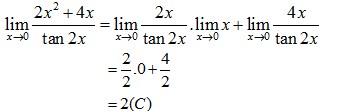
5. Nilai dari 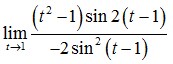   adalah …

A. 0 .

B. -¼

C. -½

D. -1

E. -2

Jawaban : E

Pembahasan :

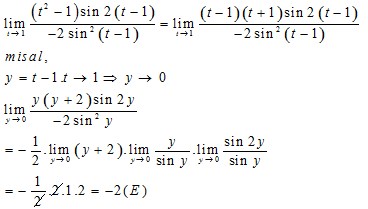
Baca Juga Soal Induksi Matematika

6. Nilai dari 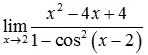   adalah …

A. -¼

B. 0 

C. ¼

D. ½

E. 1

Jawaban : E

Pembahasan :

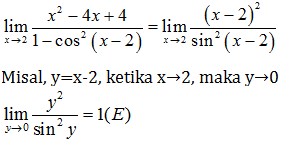
7. Nilai dari 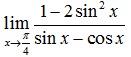   adalah …

A. √2

B. ½√2

C. 1

D. -½√2

E. -√2

Jawaban : E

Pembahasan :

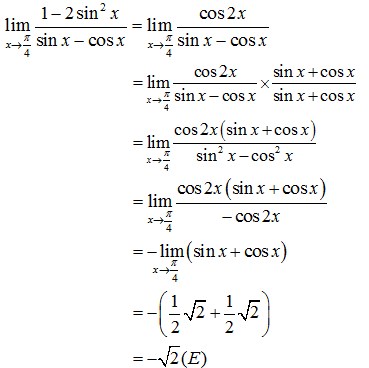
8. Nilai dari 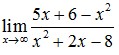  adalah …

A. -∞

B. -1

C. 1

D. 5

E. ∞

Jawaban : B

Pembahasan :

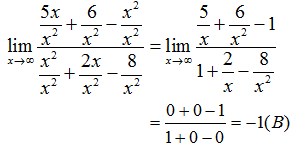
9. Nilai dari 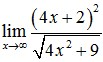adalah …

A. -∞

B. 8

C. 4

D. 2

E. 0

Jawaban : A

Pembahasan :

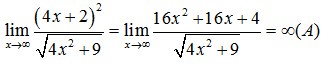
10. Jika diketahui: 

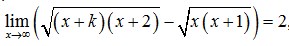
maka nilai adalah … .

A. 0 

B. 1

C. 2

D. 3

E. 4

Jawaban : D

Pembahasan :

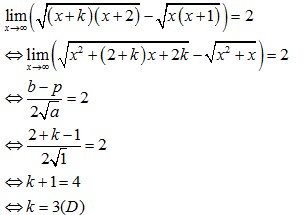
11 – 20 Soal PAS Matematika Kelas 12 Semester 1 dan Jawaban

11. Nilai dari  adalah …

A. -5/2

B. -2/5

C. 0 

D. 2/5

E. 5/2

Jawaban : E

Pembahasan :

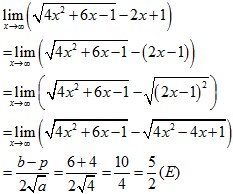
12. Nilai dari 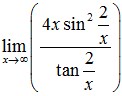  adalah …

A. -8 

B. -4

C. 0

D. 4

E. 8

Jawaban : E

Pembahasan :

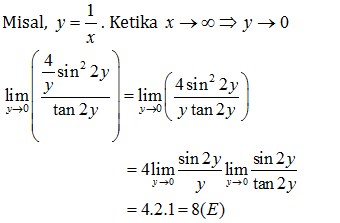
13. Asimtot tegak dan asimtot datar dari fungsi 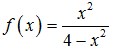   adalah …

A. ±4 dan y = -4

B. ±2 dan y = -1

C. ±2 dan y = -2

D. ±1 dan y = 1

E. ±4 dan y = 2

Jawaban : B 

Pembahasan :

14. Turunan pertama dari y = 3 sin x – cos x adalah y’ … 

A. 3 cos x – sin x

B. 3 cos x + sin x

C. cos x + sin x

D. -3 cos x – sin x

E. -3 cos x + sin x

Jawaban : B

Pembahasan :

y = 3 sin x – cos x

y’ = 3 cos x + sin x (B) 

15. Turunan pertama dari fungsi g (x) = (3x – 4) cos (2x + 1) adalah …

A. (6x – 8) sin (2x + 1) + 3 cos (2x + 1)

B. (6x – 8) sin (2x + 1) – 3 cos (2x + 1)

C. (8 – 6x) sin (2x + 1) + 3 cos (2x + 1)

D. (8 – 6x) sin (2x + 1) – 3 cos (2x + 1)

E.  (8 – 6x) sin (2x + 1) + 3x cos (2x + 1)

Jawaban : C

Pembahasan :

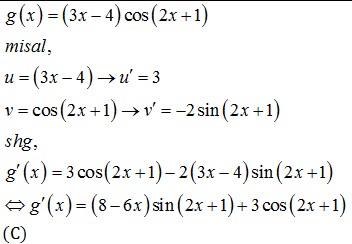
Simak Juga : Soal Pangkat, Akar, dan Logaritma

16. Turunan pertama dari fungsi

f (x) = ³√sin² 3x   adalah f'(x) =  …

Jawaban :  

Pembahasan :

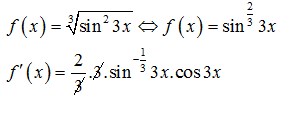
17. Turunan pertama dari fungsi p (x) = sec x + cot 3x adalah …

A. tan²  x+ 3 csc² 3x

B. sec  x. tan x+ 3 csc 3x

C. sec  x. tan x – 3 csc² 3x

D. sec²  x – 3 csc 3x

E. sec  x – 3 csc 3x

Jawaban : C

Pembahasan :

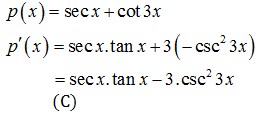
18. Turunan pertama dari fungsi:   

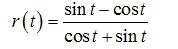
adalah r’ (t) =  …

Jawaban : D

Pembahasan :

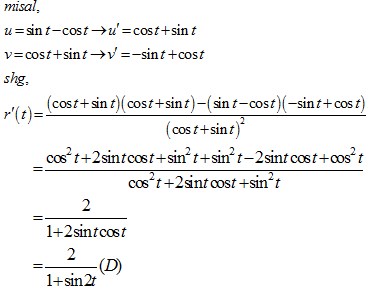
19. Jika diketahui fungsi

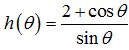
 maka nilai dari h’ (Π/3) adalah … 

A. -8/3

B. -4/3

C. 3/8

D. 3/4

E. 8/3

Jawaban : A

Pembahasan :

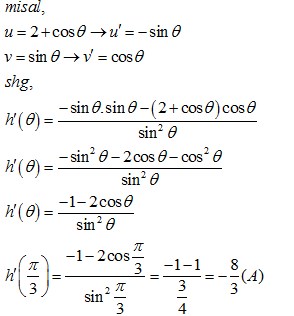
20. Turunan kedua dari fungsi h(x) = cos x – sin 3 x  adalah h’ (x) = … 

A. sin x – 3 cos 3x

B. – sin x – 3 cos 3x

C. cos x – 9 cos 3x

D. -cos x – 9 sin 3x

E. -cos x + 9 sin 3x

Jawaban : E

Pembahasan :

h(x) = cos x – sin 3 x

h'(x) = – sin x – 3 cos 3x

h”(x) = – cos x + 9 sin 3x (E)

Baca Juga Soal Persamaan Kuadrat

21 – 30 Contoh Soal PAS Matematika Pilihan Ganda dan Jawaban

21. Nilai kemiringan garis singgung pada kurva y = cos x + 2 di titik yang berbasis π/3 adalah … 

A. 2 – ½√3

B. – 1

C. – ½√3

D. ½√3

E. 2 + ½√3

Jawaban : C

Pembahasan :

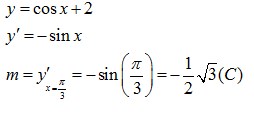
22. Nilai kemiringan garis singgung pada kurva y = 3 sin x pada titik yang berbasis π/3 adalah … 

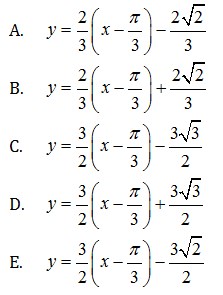
Jawaban : D

Pembahasan :

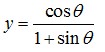
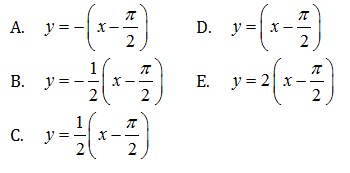
23. Persamaan garis normal pada kurva  pada titik yang berbasis θ = π/2 adalah … 

Jawaban : E

Pembahasan :

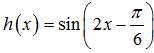
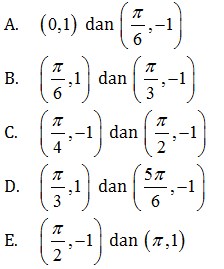
24. Titik stasioner fungsi   pada interval 0 ≤ x ≤ π adalah …

Jawaban : D

Pembahasan :

25. Fungsi f (x) = sin x – cos x untuk 0 < x < 2π naik pada interval … 

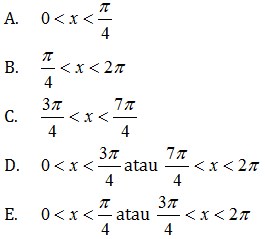
Jawaban : D

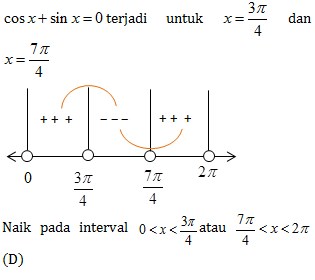
Pembahasan :

f'(x) = cos x + sin x

Nilai stasioner fungsi f (x), yaitu f’ (x) = 0 .

26. Fungsi s(t) = sin 2t untuk 0° < t < 360° akan cekung ke bawah pada interval … 

A. 0° < t < 90° atau 120° < t < 180° 

B. 0° < t < 90° atau 180° < t < 270° 

C. 0° < t < 90° atau 270° < t < 360° 

D. 90° < t < 180° atau 270° < t < 360° 

E. 90° < t < 180° atau 300° < t < 360° 

Jawaban : D

Pembahasan :

s(t) = sin 2t

s'(t) = 2 cos 2t

s”(t) = -4 sin 2t

Kita cari batas kecekungan dengan mengambil

s”(t) = -4 sin 2t = 0

27. Diketahui fungsi p (x) = 4 cos x + cos 2x  dengan 0 < x < 2π Koordinat titik belok dari fungsi tersebut adalah …

A. (π/2 , 0)

B. (π/2, -1)

C. (π, -1)

D. (π. -2)

E. (π, -3)

Jawaban : E

Pembahasan :

Nilai stasioner fungsi p(x) yaitu p'(x) = 0, sehingga diperoleh

– 4 sin x (1 + cos x ) = 0

sin x = 0 atau cos x = -1

x = 0, π, 2π     atau  x = π

28. Sebuah partikel bergerak mengikuti sebuah lintasan yang dinyatakan dengan rumus s = 6 cos 3t + sin² t + t² + 5 (dalam m). Jika waktu yang ditempuh dalam  detik, maka kecepatan pada saat  detik adalah … m/detik

A. (18 + π)

B. (15 + π)

C. (11 + π)

D. (6 + π)

E. (5 + π)

Jawaban : A

Pembahasan :

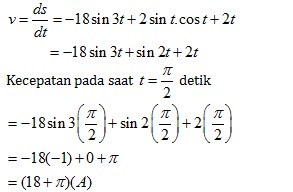
29. Nilai maksimum dan minimum dari fungsi q (x) = 2 sin (3x + 5) + 1 pada interval 0° < t < 180° adalah …

A. 2 dan 1

B. 2 dan -1

C. 3 dan 1

D. 3 dan -1

E. 4 dan -1

Jawaban : D

Pembahasan :

30. Perhatikan gambar berikut!

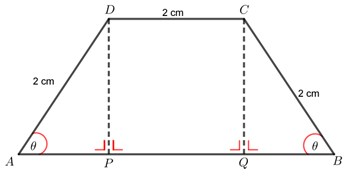
Pada gambar trapesium sama kaki ABCD, ∠DAB = ∠CBA = θ radian dengan sudut lancip. Jika luas trapesium sama kaki ABCD dinyatakan dengan fungsi t (θ) = 4 sin θ (1 + cos θ), maka pernyataan berikut yang benar adalah …

A. Luas minimumnya adalah  3√3 cm²

B. Luas maksimumnya adalah 3√3 cm²

C. Luas minimumnya adalah (2 + √3) cm²

D. Luas maksimumnya adalah (2 + √3) cm²

E. Luas maksimum atau minimum tidak dapat ditentukan

Jawaban : B

Pembahasan :

Sudah selesai membaca dan berlatih soal ini ? Ayo lihat dulu Soal Matematika lainnya

Posting terkait:

Contoh Soal Barisan dan Deret Aritmatika [Update 50 Butir]

Contoh Soal Lingkaran Kelas 8 SMP dan Jawaban [Update]

65+ Contoh Soal Limit Fungsi Aljabar dan Jawaban [Update]