Teori Relativitas Khusus – Konsep, Postulat dan Aplikasinya – Siapa yang tidak mengenal formula Einstein E = m c2 atau paradoks si kembar yang mendapati saudara kembarnya sudah jauh lebih tua setelah ia melakukan perjalanan dengan kecepatan mendekati kecepatan cahaya? Namun tidak semua orang tahu kalau “keajaiban” tersebut hanyalah bagian kecil dari teori relativitas Einstein, serta bagaimana sebenarnya Einstein mendapatkan teori relativitas tersebut.

Pada tahun 1905, Einstein menerbitkan sebuah makalah mengenai elektrodinamika benda bergerak, di dalamya Einstein membuat dua asumsi sederhana.
- Asumsi pertama, adalah asas relativitas. Menurut asas ini, tidak mungkin untuk membedakan satu system dari system yang lain jika kedua-duanya bergerak dengan kecepatan tetap (tidak dipercepat).
- Asumsi kedua, kecepatan cahaya dalam ruang kosong adalah tetap, bebas dari gerakan sumber cahaya maupun pengamat. (Gerry, 2004). Ternyata gagasan ini menuntut revolusi dalam konsep ruang dan waktu.
Simak Juga : Soal Teori Relativitas Khusus dan Jawaban
A. Konsep Teori Relativitas
Pada tahun 1915 Albert Einstein mempublikasikan sebuah teori yang kemudian disebut Teori Relativitas Umum oleh Akademi Sains Prussia. Teori-teori Einstein merupakan hal baru dalam dunia fisika saat itu dan beberapa bagian menyanggah teori Newton.
Teori Relativitas Umum menggambarkan alam semesta sebagai hubungan antara materi dan geometri ruang-waktu (spacetime). John Wheler menyederhanakan Teori Relativitas Umum Einstein ini dalam satu kalimat:
- materi membuat ruang-waktu melengkung (curved),
- dan ruang-waktu membuat materi bergerak (motion).
Kombinasi geometri-materi inilah yang kita rasakan sebagai gravitasi. Teori Relativitas Umum menjelaskan interaksi pada skala makro atau tingkat kasat mata, misalnya peredaran planet, bintang, dan galaksi.
Konsep relativitas khusus memandang ruang-waktu sebagai jalinan koordinat mirip sehelai permadani yang dibentangkan di lantai, alias datar. Dua tahun kemudian, Eisntein tidak bisa mempertahankan anggapan ruang-waktu yang datar ini ketika ia mencoba menerapkan kaitan antara relativitas khusus dan gravitasi. Akhirnya setelah memainkan matematika yang cukup rumit dan dengan menganggap bahwa cahaya adalah partikel yang sebenar-benarnya (foton) hingga bisa dipengaruhi gravitasi, didapatkanlah relativitas umum, yang dirumuskan Einstein di tahun 1916 dan demikian menggemparkan.
Pada intinya, ketika di ruang-waktu terdapat obyek yang cukup masif atau padat (seperti planet, bintang-bintang dan galaksi), ruang-waktu akan melengkung (mirip mangkok) dan itulah yang disebut gravitasi. Pada masa kini, selain mekanika kuantum, relativitas umum adalah permata nya fisika, yang sanggup menjelaskan perilaku alam semesta dalam struktur berskala besar. Penemuan black hole yaitu bintang bergravitasi sangat besar hingga mampu menyerap seluruh cahayanya sendiri terkait erat dengan teori gravitasi Einstein ini.

Gambar 1
Konsep Ruang-waktu dalam Teori Relativitas Umum. Massa mempengaruhi bentuk kontur dimensi ruang-waktu, dan bentuk kotur dimensi ruang-waktu mempengaruhi massa untuk bergerak
Teori Relativitas Umum membuat geger karena menyanggah Persamaan Gravitasi Hukum Newton bahwa gravitasi bukanlah sebuah gaya namun hanya konsekuensi dari akibat pelengkungan ruang-waktu. Waktu menjadi parameter bersama ruang tiga dimensi membentuk ruang-waktu atau spacetime, ruang-waktu memiliki referensi terhadap kejadian (event) yang secara matematis disimbolkan dengan koordinat (t, x, y, z) atau dalam koordinat angular (t, r, θ, dan φ).
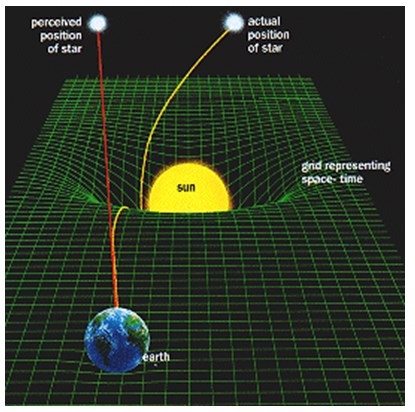
Gambar 2
Menurut teori relativitas umum ruang-waktu tidak datar tetapi melengkung karena cahaya sebagai foton dipengaruhi oleh gravitasi. Cahaya bintang yang sampai ke bumi dipengaruhi oleh gravitasi matahari (ditarik ke arah matahari) sehingga orang melihat letak bintang tidak pada tempat yang semestinya (garis kuning) tetapi berada pada posisi semu (garis merah)
Teori Relativitas Umum tidak dibahas lebih lanjut dalam materi melainkan Teori Relativitas Khusus. Melihat riwayat teori relativias umum ini saja, merujuk pada kata-kata Sir Arthur Eddington di tahun 1930-an, pada saat itu hanya ada 3 orang di dunia yang bisa memahami relativitas umum, yakni Einstein dan Eddington sendiri, serta orang muda India yang saat itu sedang berlayar ke Inggris untuk menuntut ilmu di Cambridge Inggris di bawah asuhan Eddington bernama Subrahmanyan Chandrasekhar.
B. Relativitas Newton
Teori relativitas muncul dari kebutuhan terhadap kerangka acuan, yaitu suatu patokan yang dapat digunakan ilmuwan untuk menganalisis hukum gerak. Pada waktu kelas X, kalian telah mempelajari Hukum Newton tentang gerak, di mana Hukum I Newton tidak membedakan antara partikel yang diam dan partikel yang bergerak dengan kecepatan konstan. Jika tidak ada gaya luar yang bekerja, partikel tersebut akan tetap berada dalam keadaan awalnya, diam atau bergerak dengan kecepatan awalnya.
Benda akan dikatakan bergerak apabila kedudukan benda tersebut berubah terhadap kerangka acuannya. Kerangka acuan di mana Hukum Newton berlaku disebut kerangka acuan inersia. Jika kita memiliki dua kerangka acuan inersia yang bergerak dengan kecepatan konstan relatif terhadap yang lainnya, maka tidak dapat ditentukan bagian mana yang diam dan bagian mana yang bergerak atau keduanya bergerak. Hal ini merupakan konsep Relativitas Newton, yang menyatakan “gerak mutlak tidak dapat dideteksi”.
Konsep ini dikenal oleh para ilmuwan pada abad ke-17. Tetapi, pada akhir abad ke-19 pemikiran ini berubah. Sejak saat itu konsep relativitas Newton tidak berlaku lagi dan gerak mutlak dideteksi dengan prinsip pengukuran kecepatan cahaya.
Transformasi Galileo
Pada sudut pandang klasik atau Galileo, jika terdapat dua kerangka acuan S dan S′ yang masing-masing dicirikan dengan sumbu koordinat yang ditunjukkan Gambar :
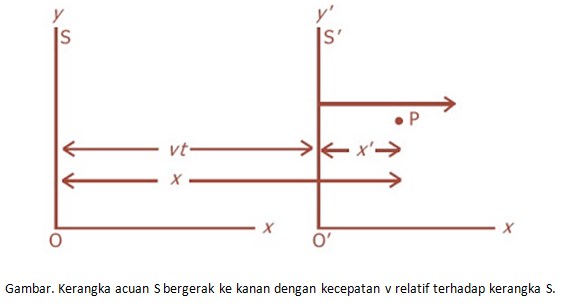
Sumbu x dan x’ saling berimpitan, dan diasumsikan kerangka S′ bergerak ke kanan (arah x) dengan kecepatan v relatif terhadap S. Untuk menyederhanakan, diasumsikan bahwa acuan O dan O’ dari kedua kerangka acuan saling berimpit pada t = 0.’
Sekarang, dimisalkan terjadi sesuatu di titik P yang dinyatakan dalam koordinat x ‘, y ‘, z’ dalam kerangka acuan S’ pada saat t’. Bagaimana koordinat P di S? Perlu diketahui, karena S dan S’ mula-mula berimpitan, setelah t, S’ akan bergerak sejauh vt’. Sehingga pada saat t ‘ akan berlaku:
x = x’ + vt’ …………………………………………….. (1)
y = y’…………………………………………………….. (2)
z = z’ ……………………………………………………. (3)
t = t ‘…………………………………………………….. (4)
Persamaan-persamaan tersebut dinamakan persamaan transformasi Galileo. Jika titik P pada Gambar 10.2 menunjukkan sebuah benda yang bergerak, maka komponen vektor kecepatannya di S’ dimisalkan ux‘, uy‘, uz‘. Diperoleh ux’ = Dx’/Dt’, uy’ = Dy’ /Dt’, dan uz‘ = Dz’ /Dt’. Jika pada t1‘ partikel berada di x1′ dan sesaat kemudian, t2 berada di x2′, diperoleh:
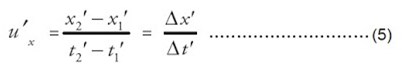
Jadi, kecepatan P seperti terlihat dari S akan memiliki komponen ux, uy, dan uz. Untuk komponen yang berhubungan dengan komponen kecepatan di S’ diperoleh:
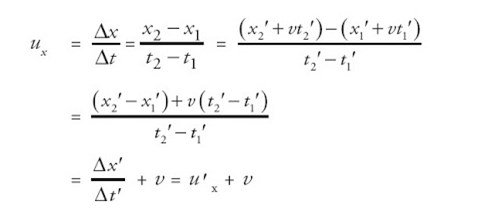
Dapat disimpulkan bahwa:
ux = ux‘ + v ………………………………………………… (6)
uy = uy‘ ……………………………………………………… (7)
uz = uz‘ ………………………………………………………. (8)
yang merupakan persamaan transformasi kecepatan Galileo
C. Percobaan Michelson-Morley
Pada tahun 1887, Albert Michelson (1852 – 1931) dan Edward Morley (1838 – 1923) melakukan suatu percobaan untuk mengukur kecepatan bumi dengan eter, yaitu suatu medium hipotetik yang dahulu diyakini diperlukan untuk membantu perambatan radiasi elektromagnetik. Dengan menggunakan interferometer Michelson, mereka berharap dapat mengamati suatu pergeseran pada pita interferensi yang terbentuk saat alat diputar 90°, untuk menunjukkan bahwa laju cahaya yang diukur pada arah rotasi bumi, atau arah lintasan orbit, berbeda dengan laju pada arah 90° terhadap arah rotasi.
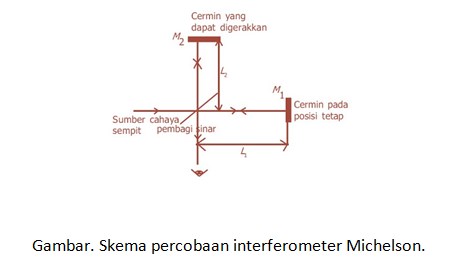
Dalam percobaan ini, yang ditunjukkan pada Gambar 1, satu berkas cahaya bergerak menurut arah gerak Bumi dan yang lain bergerak tegak lurus terhadap gerak ini. Perbedaan antara waktu tempuh berkas tergantung pada kecepatan Bumi dan dapat ditentukan dengan pengukuran interferensi.
Kita anggap interferometer tersebut diarahkan sedemikian rupa, sehingga berkas yang mengenai cermin M1 berada dalam gerak Bumi yang diandaikan. Berkas yang memantul dari pembagi berkas dan mengenai cermin M2 bergerak dengan kecepatan tertentu (relatif terhadap Bumi) yang tegak lurus terhadap kecepatan bumi. Kedua sinar dari cermin M1 dan M2 akan sampai pada pengamat. Jika ada eter yang bergerak dengan kelajuan v, maka akan timbul perbedaan waktu sebesar:
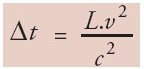
Dengan c menyatakan kecepatan cahaya.
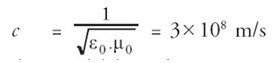
dan L adalah jarak cermin pada pembagi sinar
Perbedaan waktu tersebut dapat dideteksi dengan mengamati interferensi dari kedua berkas cahaya tadi. Pita interferensi yang diamati dalam kedudukan pertama haruslah mengalami pergeseran. Akan tetapi, pada kenyataannya, tidak ditemukan adanya pergeseran.
Percobaan yang sama dilakukan dengan berbagai keadaan, dan hasil yang diperoleh menunjukkan tetap tidak ditemukan adanya pergeseran. Jadi, dapat disimpulkan bahwa hipotesis yang menyatakan keberadaan eter tidak benar, dalam arti bahwa eter tidak ada.
D. Postulat Teori Relativitas Khusus
Transformasi Lorentz
- Postulat 1
“hukum-hukum fisika adalah sama dalam semua kerangka inersia”, postulat ini merupakan perluasan prinsip relativitas Newton untuk mencakup semua jenis pengukuran fisis, bukan hanya mekanis.
- Postulat 2
“ kelajuan cahaya adalah sama dalam semua kerangka inersia”, postulat pertama karena tidak adanya acuan universal sebagai acuan mutlak. Postulat kedua memiliki implikasi yang sangat luas dengan kecepatan, panjang, waktu dan massa benda yang semuanya bersifat relative.
Transformasi Galileo hanya berlaku jika kecepatan-kecepatan yang digunakan tidak bersifat relativistic, yaitu jauh lebih kecil dari kecepatan cahaya. Sesuai dengan teori relativitas bahwa kecepatan cahaya di S juga adalah c. maka diperlukan persamaan transformasi baru untuk bisa melibatkan kecepatan relativistic.
Dengan adanya Transformasi Lorentz, masalah perbedaan panjang, massa,dan waktu, antara di Bumi dan di luar angkasa dapat terpecahkan.
Kita asumsikan transformasi bersifat linier dalam bentuk :
X = ɤ(x’+vt’)………………….. (10.10)
Y = y’………………………………..(10.11)
Z = z’ ……………………………….(10.12)
Kita asumsikan bahwa y dan z tidak berubah karena diperkirakan tidak terjadi kontraksi panjang pada arah ini. Persamaan invers harus memiliki bentuk yang sama dimana v diganti dengan –v, sehingga
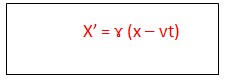
Maka diperolah ɤ :
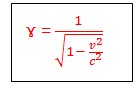
Dengan kata lan dapat disimpulkan:

Dilatasi Waktu
Akibat penting postulat Einstein dan transformasi Lorentz adalah bahwa selang waktu antara dua kejadian yang terjadi pada tempat yang sama dalam suatu kerangka acuan selalu lebih singkat daripada selang waktu antara kejadian sama yang diukur dalam kerangka acuan lain yang kejadiannya terjadi pada tempat yang berbeda.
Pada dua kejadian yang terjadi di x0‘ pada waktu t1‘ dan t2‘ dalam kerangka S ‘, kita dapat menentukan waktu t1 dan t2 untuk kejadian ini dalam kerangka S dari persamaan (9). Kita peroleh:
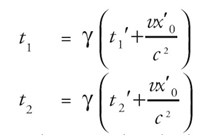
Sehingga, dari kedua persamaan tersebut diperoleh:
t2 – t1 = γ (t2‘ – t1‘) ……………………………………… (13)
Waktu di antara kejadian yang terjadi pada tempat yang sama dalam suatu kerangka acuan disebut waktu patut, tp. Dalam hal ini, selang waktu Δtp = t2‘ – t1‘ yang diukur dalam kerangka S’ adalah waktu patut. Selang waktu Δt yang diukur dalam kerangka sembarang lainnya selalu lebih lama dari waktu patut. Pemekaran waktu ini disebut dilatasi waktu, yang besarnya:
Δt = γ.Δtp …………………………………………….. (14)
Kontraksi Panjang
Kontraksi panjang adalah penyusutan panjang suatu benda akibat gerak relatif pengamat atau benda yang bergerak mendekati cepat rambat cahaya. Penyusutan panjang yang terjadi merupakan suatu fenomena yang berhubungan dengan pemekaran waktu. Panjang benda yang diukur dalam kerangka acuan di mana bendanya berada dalam keadaan diam disebut panjang patut (panjang benda menurut pengamat), l. Kita tinjau sebatang tongkat dalam keadaan diam di S’ dengan satu ujung di x2‘ dan ujung lainnya di x1‘ , seperti pada Gambar . Panjang tongkat dalam kerangka ini adalah l = x2‘ – x1‘.
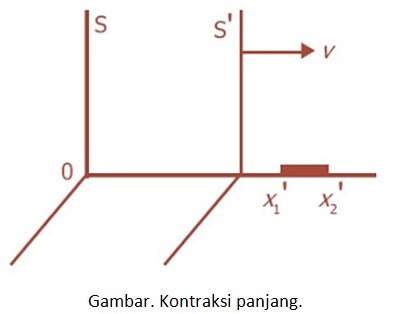
Untuk menentukan panjang tongkat di kerangka S, didefinisikan bahwa l = x2 – x1. Berdasarkan invers dari persamaan (18) akan diperoleh:
x2‘ = γ (x2 – vt2) …………………………………………. (15)
dan
x1‘ = γ (x1 – vt1) …………………………………………. (16)
Karena waktu pengukuran x1 sama dengan waktu pengukuran x2, maka t1 = t2, sehingga:
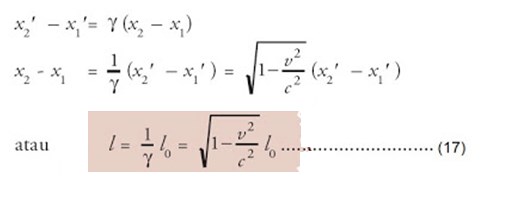
dengan l0 adalah panjang benda sebenarnya, v adalah kecepatan benda, c adalah cepat rambat cahaya, dan l adalah panjang benda menurut pengamat. Adanya dilatasi waktu yang dipengaruhi oleh gerak benda relatif, akan memengaruhi pengukuran panjang. Panjang benda yang bergerak terhadap pengamat kelihatannya lebih pendek daripada panjang sebenarnya.
E. Massa ,Momentum, dan Energi Relativistik
Massa Relativistik
Menurut teori relativitas khusus bahwa massa relativistik m dari sebuah partikel yang bergerak dengan laju v terhadap pengamat dinyatakan:
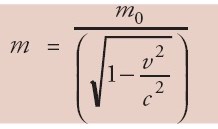
Dengan m0 adalah massa diam, yaitu massa yang diukur bila partikel tersebut berada dalam keadaan diam (v = 0) dalam suatu kerangka acuan, dan m disebut massa relativistik partikel.
Momentum Relativistik
Momentum suatu partikel didefinisikan sebagai perkalian massa dan kecepatannya. Berdasarkan hukum kekekalan momentum linier dalam relativitas umum, maka didefinisikan kembali momentum sebuah partikel yang massa diamnya m0 dan lajunya v adalah:
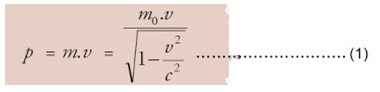
Energi Relativistik
Dalam mekanika klasik, usaha yang dilakukan oleh gaya yang bekerja pada partikel sama dengan perubahan pada energi kinetik partikel tersebut. Sebagaimana dalam mekanika klasik, kita akan mendefinisikan energi kinetik sebagai kerja yang dilakukan oleh gaya dalam mempercepat partikel dari keadaan diam hingga mencapai kecepatan tertentu. Jadi,
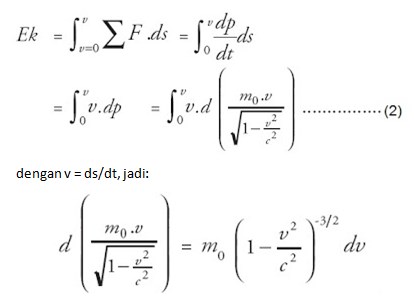
Kemudian, persamaan tersebut disubstitusikan ke persamaan (2), maka diperoleh:
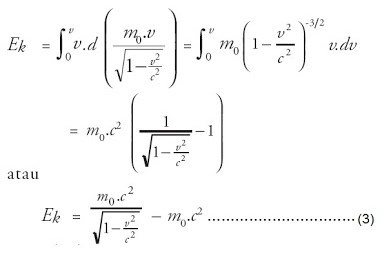
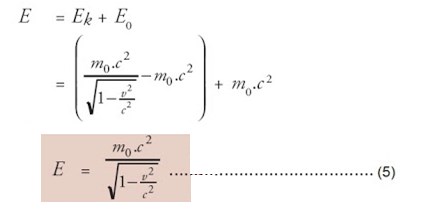
Suku kedua persamaan (3) tidak bergantung pada kecepatan dan disebut energi diam partikel E0, yang merupakan perkalian massa diam dengan c2 .
E0 = m0 . c2 ………………………………………………. (4)
Jumlah energi kinetik dan energi diam disebut energi relativistik, yaitu :
F. Aplikasi Teori Relativitas Khusus
Albert Einstein pada tahun 1905 menyatakan bahwa ada kesetaraan antara massa dan energi pada benda yang bergerak mendekati kecepatan cahaya. Pada penyinaran zat radioaktif, selalu disertai energi yang sangat besar. Energi ini diserap dan berubah menjadi panas. Jika benda diam menerima energi kinetik, massa relatif benda akan bertambah. Tetapi, jika kehilangan energi, massa benda relatif akan berkurang. Einstein merumuskan bahwa energi sebanding dengan massa dan kuadrat kecepatan cahaya, yang dinyatakan:
E = m.c2 ……………………………………………….. (1)
Dalam fisika klasik kita mengenal dua prinsip kekekalan, yaitu kekekalan massa (klasik) dan kekekalan energi. Dalam relativitas, kedua prinsip kekekalan tersebut bergabung menjadi prinsip kekekalan massa-energi, dan memegang peranan penting dalam reaksi inti.
Pada sebuah atom hidrogen mempunyai massa diam 1,00797 u setara dengan 938,8 MeV. Jika tenaga yang mencukupi (13,58 eV) ditambahkan untuk mengionisasi hidrogen tersebut, yaitu untuk memecahkan hidrogen menjadi bagian-bagian pembentuknya (proton dan elektron), maka perubahan pecahan massa diam sistem tersebut adalah:
13,58 eV / 938,8 106 eV = 1,45× 10-8.
Nilai itu setara dengan 1,45 × 10-6 persen, yang terlalu kecil untuk diukur. Tetapi, untuk sebuah inti seperti deuteron dengan massa diam 2,01360 u yang setara dengan 1876,4 MeV, maka diperlukan tambahan tenaga sebesar 2,22 MeV untuk memecahkan deuteron tersebut menjadi bagian pembentuknya. Perubahan pecahan massa diam sistem tersebut adalah:
2,22 MeV / 1876,4 MeV = 1,18 × 10-3
atau sekitar 0,12 persen, sehingga dengan mudah dapat diukur. Hal ini merupakan ciri perubahan massa diam pecahan dalam reaksi nuklir, sehingga hukum kekekalan energi-massa harus digunakan dalam suatu eksperimen reaksi nuklir, agar diperoleh kesesuaian dengan teorinya.
Reaksi fisi adalah reaksi pembelahan inti berat menjadi dua buah inti atau lebih yang lebih ringan, disertai pancaran energi yang sangat besar. Sementara itu, reaksi fusi merupakan reaksi penggabungan beberapa inti ringan, disertai pengeluaran energi yang sangat besar. Proses ini merupakan kebalikan dari fisi, tetapi hasil terakhir sama yaitu energi yang dahsyat.
Sudah selesai membaca materi ini ? Ayo lihat dulu Daftar Materi Fisika



