Gerak Melingkar Beraturan – Pengertian, Rumus, Besaran dan Contohnya – Gerak Melingkar adalah gerak suatu benda yang membentuk lintasan berupa lingkaran mengelilingi suatu titik tetap. Agar suatu benda dapat bergerak melingkar ia membutuhkan adanya gaya yang selalu membelokkan-nya menuju pusat lintasan lingkaran. Gaya ini dinamakan gaya sentripetal. Suatu gerak melingkar beraturan dapat dikatakan sebagai suatu gerak dipercepat beraturan, mengingat perlu adanya suatu percepatan yang besarnya tetap dengan arah yang berubah, yang selalu mengubah arah gerak benda agar menempuh lintasan berbentuk lingkaran.

A. Pengertian Gerak Melingkar
Gerak melingkar beraturan adalah gerak yang lintasannya berbentuk lingkaran dengan laju konstan dan arah kecepatan tegak lurus terhadap arah percepatan. Sebuah benda bergerak pada garis lurus jika gaya total yang ada padanya bekerja pada arah gerak benda tersebut, atau sama dengan nol. Dengan demikian, benda yang mengelilingi sebuah lingkaran terus dipercepat, bahkan ketika lajunya tetap konstan (v1= v2= v).
Simak Juga : Contoh Soal Gerak Melingkar Pilihan Ganda dan Pembahasan
B. Besaran dalam Gerak Melingkar Beraturan
1. Periode dan Frekuensi Gerak Melingkar Beraturan
Sebuah partikel/benda yang bergerak melingkar baik gerak melingkar beraturan ataupun yang tidak beraturan, geraknya akan selalu berulang pada suatu saat tertentu. Dengan memerhatikan sebuah titik pada lintasan geraknya, sebuah partikel yang telah melakukan satu putaran penuh akan kembali atau melewati posisi semula. Gerak melingkar sering dideskripsikan dalam frekuensi ( f ), yaitu jumlah putaran tiap satuan waktu atau jumlah putaran per sekon. Sementara itu, periode (T ) adalah waktu yang diperlukan untuk menempuh satu putaran.
Hubungan antara periode (T ) dan frekuensi ( f ) adalah:
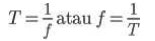
dengan:
T = periode (s)
f = frekuensi (Hz)
Untuk benda yang berputar membentuk lingkaran dengan laju konstan ν, dapat kita tuliskan:
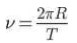
Hal ini disebabkan dalam satu putaran, benda tersebut menempuh satu keliling lingkaran (= 2 π R).
2. Posisi Sudut (θ) Gerak Melingkar Beraturan
Besar sudut satu putaran adalah 360° = 2 θ radian.
Jika θ adalah sudut pusat lingkaran yang panjang busurnya s dan jari – jarinya R, diperoleh hubungan:
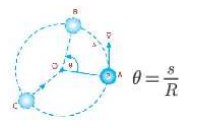
dengan:
θ = lintasan/posisi sudut (rad)
s = busur lintasan (m)
R = jari-jari (m)
3. Kecepatan Sudut/Kecepatan Angular Gerak Melingkar Beraturan
Kecepatan sudut didefinisikan sebagai besar sudut yang ditempuh tiap satu satuan waktu. Untuk partikel yang melakukan gerak satu kali putaran, didapatkan sudut yang ditempuh θ =2 π dan waktu tempuh t = T. Berarti, kecepatan sudut ( ω) pada gerak melingkar beraturan dapat dirumuskan :

dengan:
ω = kecepatan sudut (rad/s)
T = periode (s)
f = frekuensi (Hz)
4. Percepatan Sentripetal (αs)
Percepatan sentripetal didefinisikan sebagai percepatan yang selalu tegak lurus terhadap kecepatan linearnya dan mengarah ke pusat lingkaran. Percepatan sentripetal dapat dicarai dengan persamaan berikut:
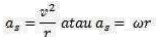
C. Rumus yang Biasanya Digunakan dalam Gerak Melingkar Beraturan :
1. Benda Yang Diputar Horizontal
Mempunyai kecepatan maksimum (vmaks) yang dibatasi oleh tegangan tali maksimum (Tmaks) agar talinya tidak sampai putus.
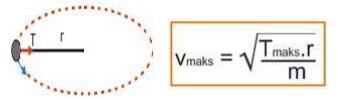
2. Ayunan Kerucut (Konis)
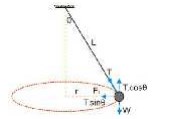
Rumus-rumus dalam ayunan kerucut :
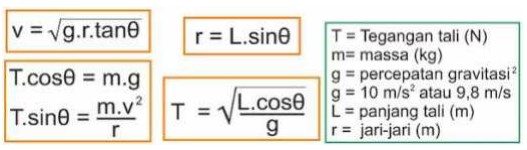
Kelajuan maksimum agar kendaraan membelok dengan baik
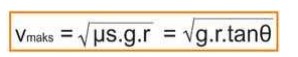
3. Sudut Kemiringan Jalan pada Belokan :
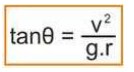
penggunaan rumus diatas ketika yang diketahui atai yang ditanyakan adalah kecepatan liniernya….namun bila yang diketahui adalah kecepatan sudutnya maka bagian rumus dibawah ini berubah menjadi :
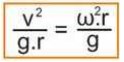
4. Gerak Melingkar Vertikal pada Seutas Tali
Penggabungan besarnya tegangan dan pengaruh berat bandul setara dengan gaya sentripetal benda (Fs).

maka tegangan tali dapat kita cari dengan memindahkan pengaruh berat benda ke ruas kanan :
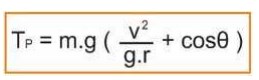
kedua rumus di atas sebenarnya sama persis, hanya terjadi peruraian rumus saja terserah yang akan kalian hafal yang mana.
bila sudah tahu prinsipnya sebenarnya tidak harus dihafal. sedangkan rumus-rumus khusus di beberapa titik sebagai berikut :
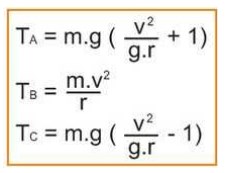
kecepatan minimum untuk :

5. Gerak Melingkar Vertikal dalam Lingkaran
Berbeda dengan gerak vertikal benda yang diikat dengan seutas tali, pada gerakan ini benda bergerak di dalam lintasan lingkaran yang vertikal atau dapat juga tempat berpijak bendalah yang berputar vertikal sementara benda tersebut berada di sebelah dalamnya.
seperti air dalam ember yang diikat tali atau pilot pesawat yang bermanuver membentuk lingkaran vertikal atau seperti contoh gambar di atas (bola dalam ember).
dalam kondisi ini berlaku rumus umum :
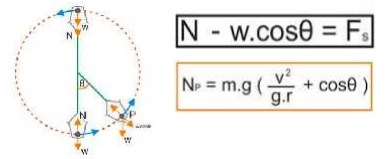
kecepatan minimal agar saat di titik tertinggi benda tidak meninggalkan lintasan :
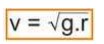
6. Gerakan Melingkar Vertikal di Luar Lingkaran
contoh gerakan ini adalah ketika sebuah kendaraan melintasi jalan yang gundukannya membentuk lingkaran.
coba kalian perhatikan, mengapa berat benda dikalikan dengan sin…dan bukannya cos…. alasannya terlihat dalam penguraian gaya berat pada gambar.
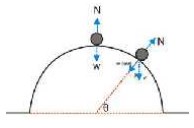
sehingga rumus umumnya :

saat di puncak berlaku :

7. Hubungan Roda – roda
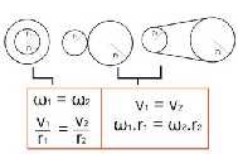
D. Ringkasan
Kita dapat menyimpulkan bahwa dalam Gerak Melingkar Beraturan :
- Besar kecepatan linear/kecepatan tangensial adalah tetap, tetapi arah kecepatan linear
selalu berubah setiap saat - kecepatan sudut (baik besar maupun arah) selalu tetap setiap saat
- percepatan sudut maupun percepatan tangensial bernilai nol
- dalam GMB hanya ada percepatan sentripetal
Sudah selesai membaca materi ini ? Ayo lihat dulu Daftar Materi Fisika



