Elastisitas – Pengertian, Sifat, Rumus dan Contohnya – Ketika Anda menarik karet mainan sampai batas tertentu, karet tersebut bertambah panjang. Jika tarikan dilepaskan, maka karet akan kembali ke panjang semula. Demikian juga ketika Anda merentangkan pegas, pegas tersebut akan bertambah panjang. Tetapi ketika dilepaskan, panjang pegas akan kembali seperti semula. Apabila di laboratorium sekolah Anda terdapat pegas, silahkan melakukan pembuktian ini. Regangkan pegas tersebut dan ketika dilepaskan maka panjang pegas akan kembali seperti semula. Mengapa demikian ? hal itu disebabkan karena benda-benda tersebut memiliki sifat elastis.
Simak Juga : 15+ Soal Elastisitas dan Hukum Hooke & Jawaban [+Pembahasan]
A. Pengertian Elastisitas
Elastisitas merupakan kecenderungan pada suatu benda untuk berubah dalam bentuk baik panjang, lebar maupun tingginya, tetapi massanya tetap, hal itu disebabkan oleh gaya-gaya yang menekan atau menariknya, pada saat gaya ditiadakan bentuk kembali seperti semula.
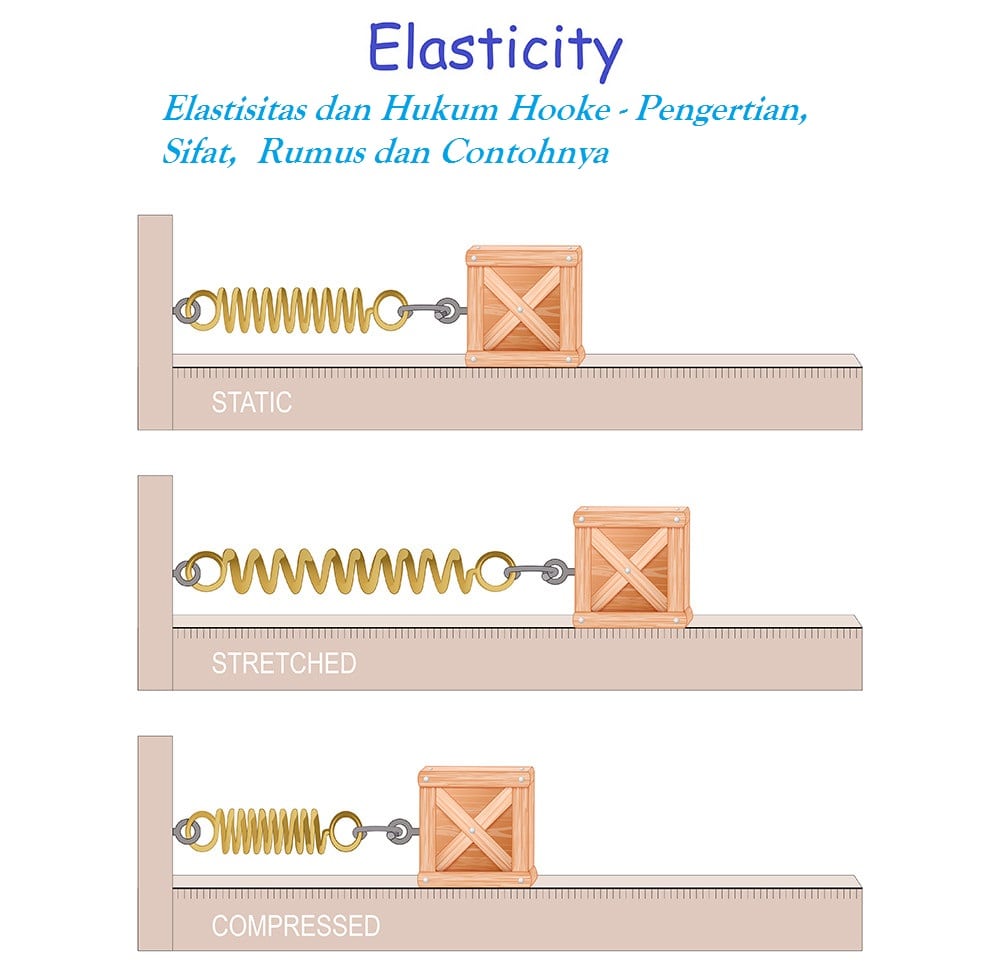
Elastis atau elastisitas dapat juga didefinisikan kemampuan sebuah benda untuk kembali ke bentuk awalnya ketika gaya luar yang diberikan pada benda tersebut dihilangkan. Jika sebuah gaya diberikan pada sebuah benda yang elastis, maka bentuk benda tersebut berubah. Untuk pegas dan karet, yang dimaksudkan dengan perubahan bentuk adalah pertambahan panjang. Perlu Anda ketahui bahwa gaya yang diberikan juga memiliki batas-batas tertentu. Sebuah karet bisa putus jika gaya tarik yang diberikan sangat besar, melawati batas elastisitasnya.
B. Sejarah Hukum Hooke
Robert Hooke (lahir 18 Juli 1635 – meninggal 3 Maret 1703 pada umur 67 tahun) adalah seorang polymath Inggris yang memainkan peranan penting dalam revolusi ilmiah, melalui kerja eksperimen dan teoretis. Dilahirkan di Freshwater di Pulau Wight, Hooke menerima pendidikan awal di Sekolah Westminster. Pada 1653, Hooke mendapatkan tempat di Christ Church, Oxford. Di sana ia bertemu dengan Robert Boyle, dan mendapat pekerjaan sebagai asistennya.

Dia berada di satu waktu bersamaan kurator percobaan dari Royal Society dan anggota dewan nya, Gresham Profesor Geometri dan Surveyor Kota London setelah Kebakaran Besar London, di mana kapasitas ia tampaknya telah melakukan lebih dari setengah dari semua survei setelah kebakaran. Hooke berperan penting dalam merancang satu set perencanaan kontrol untuk London yang pengaruhnya sampai sekarang. Allan Chapman telah ditandai sebagai “ini Inggris leonardo “.
Hooke belajar di Wadham College
selama Protektorat di mana ia menjadi salah satu dari kelompok erat merajut bersemangat royalis berpusat di sekitar John Wilkins. Di sini ia bekerja sebagai asisten Thomas Willis dan Robert Boyle, untuk siapa ia membangun pompa vakum yang digunakan dalam Boyle hukum gas eksperimen. Dia membangun beberapa yang paling awal teleskop Gregorian, mengamati rotasi Mars dan Jupiter dan, berdasarkan pengamatannya fosil, adalah pendukung awal evolusi biologis. Ia meneliti fenomena refraksi, menyimpulkan dengan teori gelombang cahaya, dan adalah yang pertama untuk menyarankan hal yang mengembang saat dipanaskan dan udara yang terbuat dari partikel-partikel kecil yang dipisahkan oleh jarak yang relatif besar.
Dia melakukan pekerjaan merintis di bidang survei dan pembuatan peta dan terlibat dalam pekerjaan yang menyebabkan peta modern pertama rencana-bentuk, meskipun rencananya untuk London pada sistem grid ditolak demi membangun kembali sepanjang rute yang ada. Dia juga datang dekat untuk menyimpulkan bahwa gravitasi mengikuti suatu hukum kuadrat terbalik , dan bahwa seperti relasi mengatur gerakan planet-planet, sebuah ide yang kemudian dikembangkan oleh Newton. Sebagian besar karya ilmiah Hooke dilakukan dalam kapasitasnya sebagai kurator percobaan dari Royal Society, sebuah pos ia diadakan dari 1662, atau sebagai bagian dari rumah tangga Robert Boyle.
Hukum Hooke
hukum atau ketentuan mengenai gaya dalam bidang ilmu fisika yang terjadi karena sifat elastisitas dari sebuah pir atau pegas. Besarnya gaya Hooke ini secara proporsional akan berbanding lurus dengan jarak pergerakan pegas dari posisi normalnya, atau lewat rumus matematis
Hukum Hooke yang ditemukan dengan rumus tanda (-) menyatakan bahwa arah F berlawanan dengan arah perubahan panjang x. Menurut Hooke , dengan x diukur dengan posisi keseimbangan pegas. Tanda (-) menunjukkan bahwa pegas diregangkan (L > 0), gaya yang dikerjakan pegas mempunyai arah sehingga menyusutkan L. Sebaliknya, waktu mendesak pegas (L < 0), gaya pegas pada arah L yang positif sedangkan k disebut konstanta pegas mempunyai dimensi gaya/panjang.
F = – kx
di mana :
- F adalah gaya (N)
- k adalah konstante pegas (N/m)
- x adalah jarak pergerakan pegas dari posisi normalnya (dalam unit meter).
Pada 1660, Hooke menemukan hukum dari elastisitas yang menyandang namanya dan yang menggambarkan variasi linier ketegangan dengan ekstensi dalam elastis semi. Dia pertama kali menggambarkan penemuan ini dalam anagram yang “ceiiinosssttuv”, yang solusinya ia diterbitkan pada 1678 sebagai “Ut Tensio, sic vis” yang berarti “Sebagai ekstensi, sehingga gaya.” Karya Hooke pada elastisitas memuncak, untuk tujuan praktis, dalam pengembangan tentang keseimbangan semi atau pegas rambut, yang untuk pertama kalinya memungkinkan sebuah arloji portabel – menonton – untuk menjaga waktu dengan akurasi yang wajar. Sebuah perselisihan sengit antara Hooke dan Christiaan Huygens pada prioritas penemuan ini adalah untuk terus selama berabad-abad setelah kematian kedua, tetapi catatan tanggal 23 Juni 1670 di Folio Hooke, menggambarkan demonstrasi keseimbangan- menonton dikendalikan sebelum Royal Society, telah diadakan untuk mendukung klaim Hooke.
Memasuki abad 20
Hal yang menarik dari sudut pandang abad kedua puluh yang pertama kali mengumumkan Hooke hukumnya elastisitas sebagai anagram. Ini adalah metode yang kadang-kadang digunakan oleh para ilmuwan, seperti Hooke, Huygens, Galileo , dan lain-lain, untuk menetapkan prioritas untuk penemuan tanpa mengungkapkan rincian.
Hooke menjadi Kurator Percobaan pada 1662 ke yang baru didirikan Royal Society , dan mengambil tanggung jawab untuk uji coba yang dilakukan pada pertemuan mingguan. Ini adalah posisi yang dipegangnya selama lebih dari 40 tahun. Sementara posisi ini terus dia di tengah-tengah ilmu pengetahuan di Inggris dan di luar, itu juga menyebabkan beberapa argumen dipanaskan dengan ilmuwan lain, seperti Huygens dan khususnya dengan Isaac Newton dan Royal Society Henry Oldenburg. Pada 1664 Hooke juga diangkat Profesor Geometry di Gresham College di London dan Dosen Cutlerian dalam Mekanika.
Pada tanggal 8 Juli 1680, Hooke mengamati pola nodal terkait dengan mode getaran pelat kaca. Dia berlari busur sepanjang tepi piring kaca ditutupi dengan tepung, dan melihat pola nodal muncul.
C. Teori Hukum Hooke
Hukum Hooke menyelidiki hubungan antara gaya F yang merenggangkan sebuah pegas dengan pertambahan panjang pegas (Δx), pada daerah batas elastisitas pegas. Pada daerah elastisitasnya, Besar gaya luar yang dibrikan (F) sebanding dengan pertambahan panjang pegas (Δx).

Persamaan hukum Hooke
Dari bunyi hukum Hooke di atas, hukum Hooke dapat dituliskan :
F = K . Δx atau K = F / Δx
Dimana:
F : besar gaya luar yang diberikan pada Pegas (N)
Δx : Pertambahan panjang pegas (m)
K : Konstanta Pegas (N/m)
Ketika sebuah pegas diberi gaya luar dengan ditarik, maka pegas akan mengeluarkan gaya yang besarnya sama dengan gaya luar yang menariknya, tetapi arahnya berlawanan (aksi = reaksi). Jika gaya yang diberikan pegas ini disebut Gaya pemulih pegas (Fp), gaya pemulih ini juga sebanding dengan pertambahan panjang pegas Δx. Secara matematis dapat
ditulis :
Fp = – K . Δx
Dari persaman persamaan di atas, dapat ditarik kesimpulan bahwa didalam batas elastisitas benda, gaya F sebanding dengan pertambahan panjang benda. Pernyataan inilah yang dikenal dengan Hukum Hooke.
Hukum Hooke adalah hukum atau ketentuan mengenai gaya yang diakibatkan oleh sifat elastisitas suatu bahan pegas atau peer. Besarnya hukum Hooke akan sebanding dengan ertambahan panjang pegas diukur dari posisi setimbangnya. Secaara matematis hukum Hooke dapat dituliskan :
F = – k . Δx
Dimana:
F : gaya luar yang diberikan (N)
k : konstante pegas (N/m)
Δx : pertambahan panjang pegas dari posisi normalnya (m)
D. Aplikasi Hukum Hooke
1. Neraca
Neraca yang dalam bahasa sehari – hari disebut timbangan . Neraca terdiri dari beberapa jenis, salah satunya adalah neraca pegas yang memanfaatkan teori hukum Hooke dalam aplikasinya. Neraca pegas digunakan untuk mengetahui massa tubuh seseorang.
2. Dinamometer
Dinamometer merupakan alat ukur gaya. Di dalam dinamometer terdapat pegas. Pegas akan bertambaha panjang ketika dinamometer diberi gaya. Hal ini sesuai dengan teori hukum Hooke.
3. Ketapel
Ketapel biasa digunakan anak – anak untuk membidik buah ataupun burung yang ada di atas. Cara penggunaan ketapel ialah batu yang akan digunakan untuk membidik diletakkan di ujung karet kemudian karet ditarik sehingga keret bertambah panjang. Setelah gaya tarik dihilangkan batu akan terlempar dan ketapel aka kembali pada panjang awal. Hal ini sesuai dengan konsep hukum Hooke.
4. Kasur Pegas
Ketika tiduran di atas kasur pegas ada gaya berat yang diberikan ubuh pada kasur. Akibat gaya berat tersebut pegas pada kasur akan termampatkan. Karena ada gaya emulih pada pegas maka pegas akan meregang kembali. Karena ada gesek anara pegas dan bagian dalam kasur maka peas akan berhenti bergerak. Sebagai akibat dari gaya yang diberikan pegas kita akan merasa empuk saat tiduran di atas kasur pegas.
E. Rangkaian Pegas
Susunan Seri
Saat pegas dirangkai seri, gaya tarik yang dialami tiap pegas sama besarnya dan gaya tarik ini = gaya tarik yang dialami pegas pengganti ( F1 = F2 = ….Fn). Pertambahan panjang pegas pengganti seri = total pertambahan panjang tiap – tiap pegas ( = x1 + x2 + ….. xn) maka nilai konstanta pengganti = total dari kebalikan tiap – tiap tetapan pegas ( 1/ks = 1/k1 + 1/k2 + ….1/kn ).
Susunan Paralel
Saat pegas dirangkai paralel, gaya tarik pada pegas pengganti F = total gaya tarik pada tiap pegas ( F = F1 + F2 + ….F ). Pertambahan panjang tiap pegas sama besarnya ( xtotal = x1 + x2 + ….. xn ) maka nilai konstanta pengganti = total dari tetapan tiap – tiap pegas (kp = k1 + k2 + …. kn).

F. Tengangan (Stress)
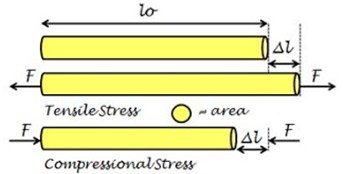
Jika sebuah benda elastis ditarik oleh suatu gaya, benda tersebut akan bertambah panjang sampai ukuran tertentu sebanding dengan gaya tersebut, yang berarti ada sejumlah gaya yang bekerja pada setiap satuan panjang benda. Gaya yang bekerja sebanding dengan panjang benda dan berbanding terbalik dengan luas penampangnya. Besarnya gaya yang bekerja dibagi dengan luas penampang didefinisikan sebagai tegangan (stress).

Apabila gaya tersebut menyebabkan pertambahan panjang pada benda, maka disebut tegangan tensil. Sebaliknya, jika gaya menyebabkan berkurangnya panjang benda, maka disebut tegangan kompresional.
G. Renggangan (Strain)
Regangan didefinisikan sebagai hasil bagi antara pertambahan panjang dengan panjang awal.
Contohnya benda yang menggantung pada tali, menimbulkan gaya tarik pada tali, sehingga tali memberikan perlawanan berupa gaya dalam yang sebanding dengan berat beban yang dipikulnya (gaya aksi = reaksi). Respon perlawanan dari tali terhadap beban yang bekerja padanya akan mengakibatkan tali menegang sekaligus juga meregang sebagai efek terjadinya pergeseran internal di tingkat atom pada partikel-partikel yang menyusun tali, sehingga tali mengalami pertambahan panjang.
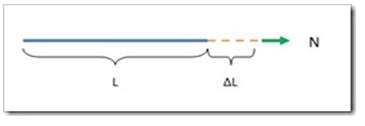
Jika tali mengalami pertambahan sejauh Δl dari yang semula sepanjang L, maka regangan yang terjadi pada tali merupakan perbandingan antara penambahan panjang yang terjadi terhadap panjang mula-mula dari tali dan dinyatakan sebagai berikut :

dimana :
ΔL = perubahan panjang (perpanjangan) …………… (satuan panjang)
L = panjang awal (panjang semula) …………… (satuan panjang)
karena pembilang dan penyebutnya memiliki satuan yang sama, maka regangan adalah sebuah nilai nisbi, yang dapat dinyatakan dalam persen dan tidak mempunyai satuan.
H. Sejarah Modulus Young
Thomas Young adalah seorang dokter Inggris dan ahli fisika, dengan pikiran yang brilian dan kepentingan eklektik. Thomas lahir di Milverton, Somerset, Inggris pada tanggal 13 Juni 1773. Pada usia empat belas dikatakan bahwa ia berkenalan dengan Latin, Yunani, Perancis, Italia, Ibrani, Arab dan Persia. Begitu besar pengetahuan bahwa ia dipanggil dipanggil Fenomena Muda oleh teman-temannya di Cambridge. Ia belajar kedokteran di London, Edinburgh, dan Göttingen dan mendirikan praktek medis di London.minat awal-nya dalam persepsi akal, dan ia adalah orang pertama yang menyadari bahwa mata memfokuskan dengan mengubah bentuk lensa. Ia menemukan penyebab astigmatisme, dan inisiator, dengan Helmoltz, dari teori warna tiga persepsi, percaya bahwa mata dibangun arti warna hanya menggunakan tiga reseptor, untuk merah, hijau dan biru. Pada 1801 ia diangkat sebagai Profesor Fisika di universitas Cambridge.

Artikel utamanya menggambarkan karakterisasi elastisitas yang kemudian dikenal sebagai modulus Young , dinotasikan sebagai E, pada tahun 1807, dan selanjutnya didituliskan dalam karya-karya berikutnya seperti 1845 Kursus Dosen Filsafat Alam dan Seni Mekanik. Namun, penggunaan pertama dari konsep modulus Young dalam percobaan adalah dengan Giordano Riccati pada tahun 1782
Modulus Young yang mengaitkan stres (tekanan) dalam tubuh untuk berhubungan strain nya (perubahan panjang sebagai rasio dari panjang asli), yaitu, stres = E × strain, untuk dimuat spesimen uniaksial. modulus Young tidak tergantung pada komponen yang diperiksa, yaitu, itu adalah aset yang material yang melekat (modulus merujuk pada sebuah aset yang material yang melekat). Modulus Young diizinkan, untuk pertama kalinya, prediksi regangan dalam subjek komponen tegangan diketahui (dan sebaliknya). Sebelum kontribusi Young, insinyur yang diperlukan untuk menerapkan F Hooke hubungan kx = untuk mengidentifikasi deformasi (x) dari suatu subjek tubuh untuk sebuah beban yang diketahui (F), di mana (k) konstan adalah fungsi dari kedua geometri dan material di bawah pertimbangan. Menemukan k diperlukan pengujian fisik untuk setiap komponen baru, sebagai F = hubungan kx merupakan fungsi dari kedua geometri dan material. Modulus Young hanya bergantung pada bahan, tidak geometri, sehingga memungkinkan sebuah revolusi dalam strategi rekayasa.
I. Teori Mudulus Young
Modulus elastisitas sering disebut sebagai Modulus Young yang merupakan perbandingan antara tegangan dan regangan aksial dalam deformasi yang elastis, sehingga modulus elastisitas menunjukkan kecenderungan suatu material untuk berubah bentuk dan kembali lagi kebentuk semula bila diberi beban (SNI 2826-2008).
Modulus elastisitas merupakan ukuran kekakuan suatu material, sehingga semakin tinggi nilai modulus elastisitas bahan, maka semakin sedikit perubahan bentuk yang terjadi apabila diberi gaya. Jadi, semakin besar nilai modulus ini maka semakin kecil regangan elastis yang terjadi atau semakin kaku
Besarnya pertambahan panjang yang dialami oleh setiap benda ketika merenggang adalah berbeda antara satu dengan yang lainnya tergantung dari elastisitas bahannya. Sebagai contoh, akan lebih mudah untuk meregangkan sebuah karet gelang daripada besi pegas. Untuk merenggangkan sebuah besi pegas membutuhkan ratusan kali lipat dari tenaga yang dibutuhkan untuk merenggangkan sebuah karet gelang.
Ketika diberi gaya tarik, karet ataupun pegas akan meregang dan mengakibatkan pertambahan panjang baik pada karet gelang ataupun besi pegas. Besarnya pertambahan yang terjadi tergantung pada elastisitas bahannya dan seberapa besar gaya yang bekerja padanya. Semakin elastis sebuah benda, maka semakin mudah benda tersebut untuk dipanjangkan atau dipendekan. Semakin besar gaya yang bekerja pada suatu benda, maka semakin besar pula tegangan dan regangan yang terjadi pada benda itu, sehingga semakin besar pula pemanjangan atau pemendekan dari benda tersebut. Jika gaya yang bekerja berupa gaya tekan, maka benda akan mengalami pemendekan, sedangkan jika gaya yang bekerja berupa beban tarik, maka benda akan mengalami perpanjangan.
Bisa disimpulkan bahwa :
regangan (ε) yang terjadi pada suatu benda berbanding lurus dengan tegangannya (σ) dan berbanding terbalik terhadap ke elastisitasannya. Ini dinyatakan dengan rumus :
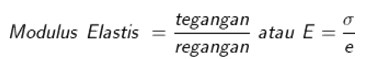
Bila nilai E semakin kecil, maka akan semakin mudah bagi bahan untuk mengalami perpanjangan atau perpendekan.
Jika kita menguraikan rumus tegangan dan regangan didapat persamaan:
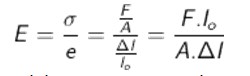
Dalam SI, satuan Modulus Young sama dengan satuan tegangan (N/m2), karena pembagian tegangan dengan regangan tidak menimbulkan pengurangan satuan (regangan tidak memiliki satuan).
Semakin besar regangan yang terjadi, maka semakin kecil nilai modulus elastisitas. Semakin besar nilai modulus suatu benda, maka semakin sulit benda tersebut dapat memanjang, dan sebaliknya.
- Jika modulus elastisitas menyatakan perbandingan antara tegangan terhadap regangan volume, maka disebut dengan Modulus Bulk yang menunjukkan besarnya hambatan untuk mengubah volume suatu benda, dan
- Jika modulus elastisitas menyatakan perbandingan antara tegangan terhadap regangan shear, maka disebut dengan Modulus Shear yang menunjukkan hambatan gerakan dari bidang-bidang benda padat yang saling bergesekan.
Dibawah ini adalah tabel yang menunjukkan nilai dari modulus elastisitas berbagai jenis benda.
| Bahan | Modulus Young | Modulus Shear | Modulus Bulk |
| (N/m2) | (N/m2) | (N/m2) | |
| Besi | 100.109 | 40. 109 | 90. 109 |
| Baja | 200. 109 | 80. 109 | 140. 109 |
| Kuningan | 90. 109 | 35. 109 | 75. 109 |
| Aluminum | 70. 109 | 25. 109 | 70. 109 |
| Beton | 20. 109 | – | – |
| Marmer | 50. 109 | – | 70. 109 |
| Granit | 45. 109 | – | 45. 109 |
| Nylon | 5. 109 | – | – |
| Tulang | 15. 109 | 80. 109 | – |
| Air | – | – | 2. 109 |
| Alkohol | – | – | 1. 109 |
| Raksa | – | – | 2. 109 |
| H2, He, CO2 | – | – | 1.01. 109 |
J. Aplikasi Modulus Young
Tiang dan Balok penyanggah pada pintu
Setiap rumah atau bangunan lainnya pasti memiliki pintu atau penghubung ruangan yang bentuknya seperti gambar di bawah. Kebanyakan bangunan menggunakan batu dan bata sebagai bahan dasar (disertai campuran semen dan pasir).
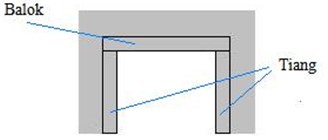
Persoalannya, batu dan bata sangat lemah terhadap tarikan dan geseran walaupun kuat terhadap tekanan. Dirimu bisa membuktikan hal ini. Jika disekitar tempatmu terdapat batu dan bata, jika batu dan bata ditumpuk(disusun secara vertikal) dalam jumlah banyak, batu dan bata tidak mudah patah (bentuknya tetap seperti semula).
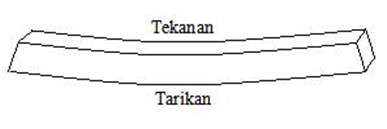
Dalam hal ini batu dan bata sangat kuat terhadap tekanan. Tetapi jika batu dan bata mengalami tegangan tarik dantegangan geser, batu dan bata mudah patah. Oleh karena itu digunakan balok untuk mengatasi masalah ini. Balok mampu mengatasi tegangan tarik, tegangan tekan dan tegangan geser. Jika anda amati balok penyanggah pada pintu rumah, tampak bahwa balok tersebut tidak berubah bentuk. Sebenarnya terdapat perubahan bentuk balok(amati gambar di bawah), hanya perubahannya sangat kecil sehingga tidak tampak ketika dilihat dari jauh. Bagian atas balok mengalami mampatan akibat adanya tegangan tekanyang disebabkan beban di atasnya (batu dan bata dkk), sedangkan bagian bawah balok mengalami pertambahan panjang (akibat tegangan tarik). Tegangan geser terjadi di dalam balok.
Sudah selesai membaca materi ini ? Ayo lihat dulu Daftar Materi Fisika



