Kesetimbangan Benda Tegar – Pengertian, Sifat, Jenis dan Contohnya – Konsep kesetimbangan benda tegar merupakan pengetahuan dasar yang sangat penting dan mempunyai banyak penerapan dalam kehidupan sehari-hari, khususnya pada bidang teknik.Pemahaman dan perhitungan mengenai gaya-gaya yang bekerja pada benda yang berada dalam keadaan setimbang statis sangat penting, khususnya bagi para ahli teknik (arsitek atau insinyur).

Dalam merancang sesuatu, baik gedung, jembatan, kendaraan, dll, para arsitek atau insinyur juga memperhitungkan secara saksama, apakah struktur suatu bangunan, kendaraan, jembatan dll, mampu menahan gaya-gaya yang bekerja padanya sehingga tidak terjadi kesalahan konstruksi pada pembangunan yang mengakibatkan bangunan tersebut mengalami kemiringan maupun ambruk.
Simak Juga : Momentum dan Impuls – Pengertian, Rumus, Hubungan dan Contoh Soal
Pengertian Kesetimbangan Benda Tegar
Dalam cabang ilmu fisika kita mengenal MEKANIKA.
Mekanika ini dibagi dalam 3 cabang ilmu yaitu :
- KINEMATIKA = Ilmu gerak
Ilmu yang mempelajari gerak tanpa mengindahkan penyebabnya. - DINAMIKA = Ilmu gaya
Ilmu yang mempelajari gerak dan gaya-gaya penyebabnya. - STATIKA = Ilmu keseimbangan
Ilmu yang mempelajari tentang keseimbangan benda.
Untuk cabang kinematika dan dinamika sudah dipelajari dikelas satu dan dua. Pada bab ini kita akan membahas mengenai STATIKA. dan benda-benda yang ditinjau pada bab ini dianggap sebagai benda tegar.
Definisi yang harus dipahami pada Statika
- Keseimbangan / benda seimbang artinya : Benda dalam keadaan diam atau pusat massanya bergerak dengan kecepatan tetap.
- Benda tegar : adalah suatu benda yang tidak berubah bentuk bila diberi gaya luar.
- Partikel : adalah benda dengan ukuran yang dapat diabaikan, sehingga benda dapat digambarkan sebagai titik dan gerak yang dialami hanyalah gerak translasi.
Momen gaya : adalah kemampuan suatu gaya untuk dapat menyebabkan gerakan rotasi. Besarnya MOMEN GAYA terhadap suatu titik sama dengan perkalian gaya dengan lengan momen.
λ = d . F
λ = momen gaya
d = lengan momen
F = gaya
Lengan momen : adalah panjang garis yang ditarik dari titik poros sampai memotong tegak lurus garis kerja gaya
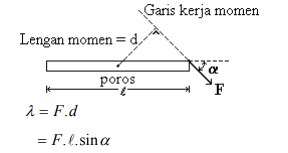
Perjanjian tanda untuk MOMEN GAYA.
- Momen gaya yang searah jarum jam bertanda POSITIF.
- Momen gaya yang berlawanan arah jarum jam bertanda NEGATIF
Koppel : adalah dua gaya yang sama besar tetapi berlawanan arah dan memiliki garisgaris kerja yang berbeda. Momen koppel terhadap semua titik sama besar, yaitu : F . d
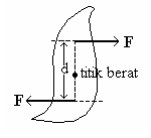
Pasangan gaya aksi – reaksi.
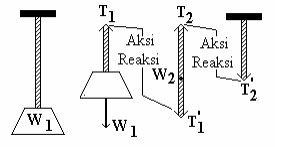
W1 = Gaya berat balok W2 = Gaya berat tali
Balok digantung dalam keadaan diam pada tali vertikal.
Gaya W1 dan T1 bukanlah pasangan aksi – reaksi, meskipun besarnya sama,
berlawanan arah dan segaris kerja. Sedangkan yang merupakan pasangan aksi – reaksi.
Macam – macam Kesetimbangan Benda Tegar
Seperti yang kita ketahui bahwa benda dapat mengalami kesetimbangan dinamis dan kesetimbangan statis. Kesetimbangan dinamis dikelompokkan menjadi dua, yaitu kesetimbangan translasi dan kesetimbangan rotasi.
Kesetimbangan translasi terjadi apabila benda bergerak dengan percepatan linier nol (a = 0), sedangkan kesetimbangan rotasi terjadi apabila benda bergerak dengan kecepatan sudut tetap atau percepatan sudut nol ( α = 0). Kesetimbangan statis benda dibedakan menjadi tiga jenis, yaitu kesetimbangan stabil, kesetimbangan labil, dan kesetimbangan netral.
Kesetimbangan Stabil
Kesetimbangan stabil atau mantap adalah kesetimbangan yang terjadi pada benda yang apabila dipengaruhi gaya akan kembali ke posisi semula, begitu gaya dihilangkan. Gambar berikut menunjukkan sebuah bola yang tergantung bebas pada sebuah tali.
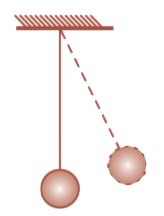
Jika bola digerakkan atau diberi gaya kemudian dihilangkan, maka bola akan segera kembali ke posisi semula. Kesetimbangan stabil ditandai dengan naiknya kedudukan titik berat benda jika dipengaruhi gaya.
Contoh :
Untuk benda yang digantung
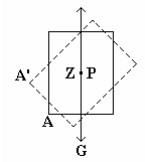
Keseimbangan stabil : apabila gaya yang diberikan padanya dihilangkan. Maka ia akan kedudukan semula. Sebuah papan empat persegi panjang digantungkan pada sebuah sumbu mendatar di P (sumbu tegak lurus papan).
Titik berat Z dari papan terletak vertikal di bawah titik gantung P, sehingga papan dalam keadaan ini setimbang stabil. Jika ujung A papan di putar sedikit sehingga titik beratnya semula (Z), maka kalau papan dilepaskan ia akan berputar kembali kekeseimbangannya semula.
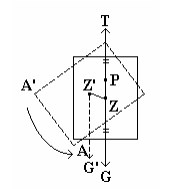
Hal ini disebabkan karena adanya suatu koppel dengan gaya berat G dan gaya tegangan tali T yang berputar kekanan. ( G = N ), sehingga papan tersebut kembali kekeseimbangannya semula yaitu seimbang stabil.
Untuk benda yang berada di atas bidang datar
Sebuah pararel epipedum siku-siku ( balok ) diletakkan di atas bidang datar, maka ia dalam keadaan ini seimbang stabil, gaya berat G dan gaya tekanan N yang masingmasing bertitik tangkap di Z ( titik berat balok ) dan di A terletak pada satu garis lurus.
Kalau balok tersebut diputar naik sedikit dengan rusuk B sebagai sumbu perputarannya, maka gaya tekanan N akan pindah ke B, dan dalam keadaan ini akan pindah ke B, dan dalam keadan ini akan timbul suatu koppel dengan gaya-gaya G dan N yang berputar ke kanan ( G = N ) sehingga balok tersebut kembali keseimbangannya semula yaitu seimbang stabil.
Kesetimbangan Labil
Kesetimbangan labil adalah kesetimbangan yang terjadi pada benda yang apabila dipengaruhi gaya tidak kembali ke posisi semula. Gambar berikut menunjukkan sebuah bola yang tergantung di atas tongkat.
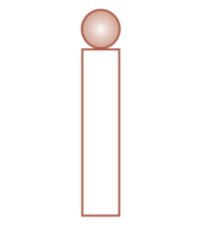
Jika bola digerakkan atau diberi gaya kemudian dihilangkan, maka bola tidak akan kembali ke posisi semula. Kesetimbangan labil ditandai dengan turunnya kedudukan titik berat benda jika dipengaruhi gaya.
Contoh :
Untuk benda yang digantung
Apabila gaya yang diberikan padanya dihilangkan, maka ia tidak akan dapat kembali ke kedudukan semula.
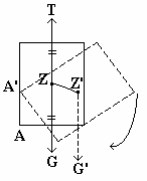
Kalau titik gantung P tadi sekarang berada vertikal di bawah titik berat Z maka papan dalam keadaan seimbang labil Kalau ujung A papan diputar sedikit naik kekiri sehingga titik beratnya sekarang ( Z’ ) di bawah titik beratnya semula ( Z ), maka kalau papan dilepaskan ia akan berputar turun ke bawah, sehingga akhirnya titik beratnya akan berada vertikal di bawah titik gantung P. Hal ini disebabkan karena adanya suatu koppel dengan gaya berat G dan gaya tekanan ( tegangan tali ) T yang berputar kekiri ( G = T ), sehingga papan turun ke bawah dan tidak kembali lagi kekeseimbangannya semula.
Untuk benda yang berada di atas bidang datar
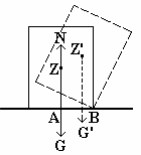
Sebuah pararel epipedum miring ( balok miring ) yang bidang diagonalnya AB tegak lurus pada bidang alasnya diletakkan diatas bidang datar, maka ia dalam keadaan ini setimbang labil, gaya berat G dan gaya tekanan N yang masingmasing melalui rusuk B dari balok tersebut terletak pada satu garis lurus.
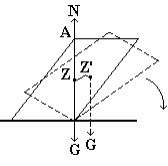
Titik tangkap gaya tekanan N ada pada rusuk N. Kalau balok tersebut diputar naik sedikit dengan rusuk B sebagai sumbu putarnya, maka gaya tekanan N yang berputar kekiri ( G = N ), sehingga balok tersebut akan turun kebawah dan tidak kembali lagi kekeseimbangannya semula.
Kesetimbangan Netral
Kesetimbangan netral atau indeferen adalah kesetimbangan yang terjadi pada benda yang apabila dipengaruhi gaya akan mengalami perubahan posisi, tetapi tidak mengalami perubahan titik berat. Gambar berikut menunjukkan sebuah bola yang berada pada lantai mendatar.
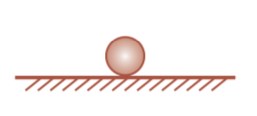
Jika bola diberi gaya kemudian dihilangkan, maka bola akan bergerak dan diam pada posisi yang berbeda. Kesetimbangan netral ditandai dengan tidak adanya perubahan (naik atau turunnya) kedudukan titik berat benda.
Contoh :
Untuk benda yang digantung
Apabila gaya yang diberikan padanya dihilangkan, maka ia
akan berada dalam keadaan keseimbangan, tetapi di tempat yang berlainan.
Kalau titik gantung P tadi sekarang berimpit dengan titik berat Z, maka papan dalam keadaan ini setimbang indiferen. Kalau ujung A papan di putar naik, maka gaya berat G dan gaya tekanan T akan tetap pada satu garis lurus seperti semula ( tidak terjadi koppel ) sehingga papan di putar bagaimanapun juga ia akan tetap seimbang pada kedudukannya yang baru.
Untuk benda yang berada di atas bidang datar
Sebuah bola diletakkan diatas bidang datar ia dalam keadaan ini seimbang indiferen.
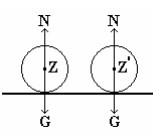
Kalau bola dipindah / diputar, maka gaya berat G dan gaya tekanan N akan tetap pada satu garis lurus seperti semula ( tidak terjadi koppel ), sehingga bola berpindah / berputar bagaimanapun juga ia akan tetap seimbang pada kedudukan yang baru.
Sudah selesai membaca materi ini ? Ayo lihat dulu Daftar Materi Fisika



