Momen Gaya dan Momen Inersia – Pengertian, Rumus dan Contohnya – Dalam gerak lurus, massa berpengaruh terhadap gerakan benda. Massa bisa diartikan sebagai kemampuan suatu benda untuk mempertahankan kecepatan geraknya. Apabila benda sudah bergerak lurus dengan kecepatan tertentu, benda sulit dihentikan jika massa benda itu besar.

Sebuah truk gandeng yang sedang bergerak lebih sulit dihentikan dibandingkan dengan sebuah taxi. Sebaliknya jika benda sedang diam (kecepatan = 0), benda tersebut juga sulit digerakan jika massanya besar. Misalnya jika kita menendang bola tenis meja dan bola sepak dengan gaya yang sama, maka tentu saja bola sepak akan bergerak lebih lambat.
Dalam gerak rotasi, “massa” benda tegar dikenal dengan julukan Momen Inersia atau MI. Momen Inersia dalam Gerak Rotasi mirip dengan massa dalam gerak lurus. Kalau massa dalam gerak lurus menyatakan ukuran kemampuan benda untuk mempertahankan kecepatan linear (kecepatan linear = kecepatan gerak benda pada lintasan lurus), maka Momen Inersia dalam gerak rotasi menyatakan ukuran kemampuan benda untuk mempertahankan kecepatan sudut (kecepatan sudut = kecepatan gerak benda ketika melakukan gerak rotasi. Disebut sudut karena dalam gerak rotasi, benda bergerak mengitari sudut). Makin besar Momen inersia suatu benda, semakin sulit membuat benda itu berputar alias berotasi. sebaliknya, benda yang berputar juga sulit dihentikan jika momen inersianya besar.
Momen Gaya
Momen gaya merupakan salah satu bentuk usaha dengan salah satu titik sebagai titik acuan. Misalnya anak yang bermain jungkat-jungkit, dengan titik acuan adalah poros jungkat-jungkit. Pada katrol yang berputar karena bergesekan dengan tali yang ditarik dan dihubungkan dengan beban. Momen gaya adalah hasil kali gaya dan jarak terpendek arah garis kerja terhadap titik tumpu. Momen gaya sering disebut dengan momen putar atau torsi, diberi lambang τ (baca: tau).
τ = F . d
Satuan dari momen gaya atau torsi ini adalah N.m yang setara dengan joule.
Momen gaya yang menyebabkan putaran benda searah putaran jarum jam disebut momen gaya positif. Sedangkan yang menyebabkan putaran benda berlawanan arah putaran jarum jam disebut momen gaya negatif.
Titik 0 sebagai titik poros atau titik acuan.
Momen gaya oleh F1 adalah τ1 = + F1 . d1
Momen gaya oleh F2 adalah τ2 = – F2 . d2
Pada sistem keseimbangan rotasi benda berlaku resultan momen gaya selalu bernilai nol, sehingga dirumuskan:
∑ τ = 0
Pada permainan jungkat-jungkit dapat diterapkan resultan momen gaya = nol.
∑ τ = 0
– F2 . d2 + F1 . d1 = 0
F1 . d1 = F2 . d2
Pada sistem keseimbangan translasi benda berlaku resultan gaya selalu bernilai nol, sehingga dirumuskan:
∑ F = 0
Pada mekanika dinamika untuk translasi dan rotasi banyak kesamaan-kesamaan besaran yang dapat dibandingkan simbol besarannya.
Contoh Soal :
Tentukan torsi di titik A, B, C, dan D pada batang homogen AD berikut!
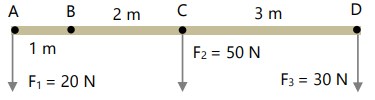
Jawaban :

Contoh Soal :
Tentukan torsi batang homogen berikut yang memiliki panjang 8 cm!
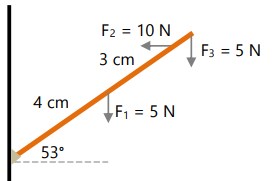
Jawaban :

Perbandingan Dinamika Translasi dan Rotasi
| Translasi | Rumus | Rotasi | Rumus |
| Momentum linier | p = mv | Momentum sudut* | L = Iω |
| Gaya | F = dp/dt | Torsi | τ = dL/dt |
| Benda massa Konstan | F = m(dv/dt) | Benda momen inersia konstan* | τ = I (dω/dt) |
| Gaya tegak lurus Terhadap momentum | F = ω x p | Torsi tegak lurus momentum sudut | τ = Ω x L |
| Energi kinetik | Ek = ½ mv2 | Energi kinetik | Ek = ½ Iω2 |
| Daya | P = F . v | Daya | P = τ . ω |
Analogi antara besaran translasi dan besaran rotasi
| Konsep | Translasi | Rotasi | Catatan |
| Perubahan sudut | s | θ | s = r.θ |
| Kecepatan | v = ds/dt | ω = dθ/dt | v = r.ω |
| Percepatan | a = dv/dt | α = dω/dt | a = r.α |
| Gaya resultan, momen | F | τ | τ = F.r |
| Keseimbangan | F = 0 | τ = 0 | |
| Percepatan konstan | v = v0 + at | ω = ω0 + at | |
| s = v0t = ½ at2 | q = ω0t + ½at2 | ||
| v2 = + 2as | ω2 = + 2θα | ||
| Massa, momen kelembaman | m | I | I = Σmiri2 |
| Hukum kedua Newton | F = ma | τ = Iα | |
| Usaha | W = ∫ F ds | W = ∫ τ dθ | |
| Daya | P = F.v | P = I ω | |
| Energi potensial | Ep = mgy | ||
| Energi kinetik | Ek = ½ mv2 | Ek = ½ Iω2 | |
| Impuls | ∫ F dt | τ ∫ dt | |
| Momentum | P = mv | L = Iω |
Momen Kopel adalah pasangan dua buah gaya yang sejajar, sama besar dan berlawanan arah. Kopel yang bekerja pada sebuah benda akan menghasilkan momen kopel yang mengakibatkan benda berotasi. Momen kopel disimbolkan M. Jika pada benda bekerja beberapa kopel maka resultan momen kopel total benda tersebut adalah
M = M1 + M2 + M3 + … + Mn Jika terdapat beberapa gaya yang bekerja pada bidang XY, maka setiap gaya tersebut dapat diuraikan atas komponen-komponennya pada sumbu-X dan sumbu-Y. Misalkan, komponen-komponen gaya pada sumbu-X adalah F1x, F2x, F3x,…,Fnx,yang jaraknya masing-masing terhadap sumbu-X adalahy1, y2, y3,…,yn. Komponen gaya pada sumbu-Y adalahF1 y , F 2y , F 3y , …,Fny , yang jaraknya masing-masing terhadap sumbu-Y adalah x1, x2, x3,…,xn. Semua komponen gaya pada sumbu-X dapat digantikan oleh sebuah gaya resultan F x yang jaraknya yo dari sumbu-X, demikian juga semua komponen gaya pada sumbu-Y dapat digantikan oleh sebuah gaya resultan F y yang jaraknya xo dari sumbu-Y.
Momen Inersia Benda Tegar
Benda tegar adalah benda padat yang tidak berubah bentuk apabila dikenai gaya luar. Dalam dinamika, bila suatu benda tegar berotasi, maka semua partikel di dalam benda tegar tersebut memiliki percepatan sudut a yang sama. Momen gaya atau gaya resultan gerak rotasi t didefinisikan sebagai berikut.
”Apabila sebuah benda tegar diputar terhadap suatu sumbu tetap, maka resultan gaya putar (torque, baca torsi) luar terhadap sumbu itu sama dengan hasil kali momen inersia benda itu terhadap sumbu dengan percepatan sudut”.
Dirumuskan sebagai berikut.
=τ Σ Fi Ri Sin qi atau τ = ( Σ mi R2 i ) . α
mSi Ri2 disebut momen inersia atau momen kelembaman benda terhadap sumbu putar, yaitu penjumlahan hasil kali massa tiap partikel dalam suatu benda tegar dengan kuadrat jaraknya dari sumbu.
Dirumuskan:
I = Σ mi . Ri2
Definisi lain dari momen inersia adalah perbandingan gaya resultan (momen) terhadap percepatan sudut.
Dirumuskan:
I =
maka τ = I . α
τ = I
Karena τ = ΣF . R dan τ = I . α
α = percepatan sudut (rad/s2)
maka ΣF . R = I . α
Percepatan tangensial adalah juga percepatan linier a, yaitu percepatan singgung tepi roda.
a = α . R
α =
persamaan menjadi :
ΣF . R = I .
Momen inersia harus dinyatakan sebagai hasil kali satuan massa dan kuadrat satuan jarak. Un tuk menghitungnya harus diperhatikan bentuk geometri dari benda tegar homogen.
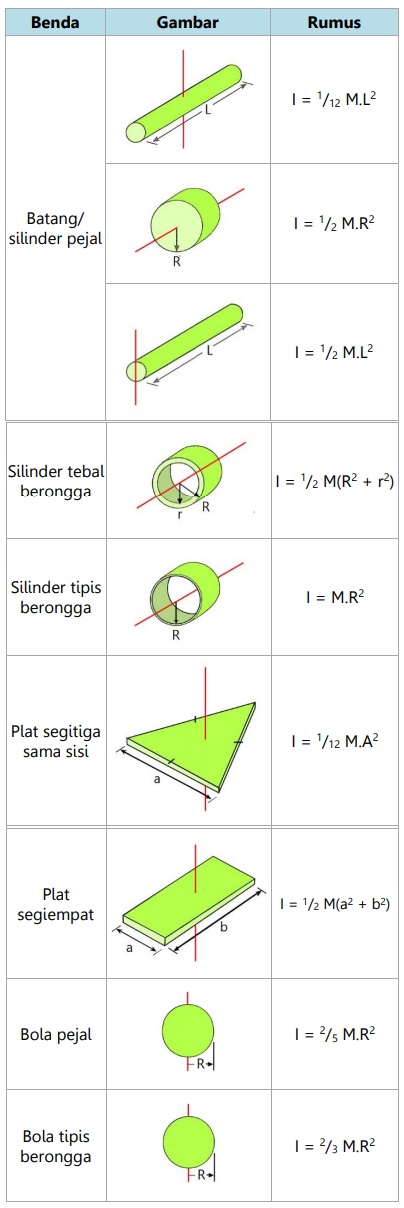
Tabel berikut menunjukkan momen inersia beberapa benda homogen.
Momen inersia berbagai benda yang umum dikenal
I = ½ M (R12 + R22) I = 1/3 MR2 I = MR2 I = 2/5 MR2 I = 2/3 MR2
Contoh :
- (1) Berapa besar momen gaya harus dikerjakan pada sistem untuk memberikan suatu percepatan µ terhadap poros ini (µ = 4 )?
- (2) Ulangi pertanyaan (a) dan (b) untuk poros AA1!
Penyelesaian:
I = Σ mi Ri2 = m1 R12 + m2 R22 + m3 R32 + m4 R42
= 3 . 22 + 2 . 22 + 1 . 22 + 2 . 22
= 12 + 8 + 4 + 8
= 32 kg m2
(1) τ = I . µ = 32 . 4 = 128 N.m
(2) I = m2 R12 + m2 R22 + m2 R22 + m3 R32 + m4R42
Daftar momen inersia dari beberapa benda tegar yang digunakan dalam perhitungan.
Momentum Sudut Gerak Rotasi Benda Tegar
Dalam dinamika, bila suatu benda berotasi terhadap sumbu inersia utamanya, maka momentum sudut total L sejajar dengan kecepatan sudut w, yang selalu searah sumbu rotasi. Momentum sudut (L) adalah hasil kali momen kelembaman I dan kecepatan sudut w. Sehingga dapat dirumuskan :
L = I . ω
Bagaimana persamaan tersebut diperoleh? Perhatikan gambar berikut. Momentum sudut terhadap titik 0 dari sebuah partikel dengan massa m yang bergerak dengan kecepatan V (memiliki momentum P = mv) didefinisikan dengan perkalian vektor,
L = R ´ P
atau L = R ´ mV
L = mR ´ V
Jadi momentum sudut adalah suatu vektor yang tegak lurus terhadap bidang yang dibentuk oleh R dan v.
Dalam kejadian gerak melingkar dengan 0 sebagai pusat lingkaran, maka vektor R dan v saling tegak lurus.
V = ω R
Sehingga L = m R v
L = m R ωR
L = m R2 ω
Arah L dan ω adalah sama, maka:
L = m R2 ω
atau L = I ω
karena ω =
maka : L = m R2
L = I
Momentum sudut sebuah partikel, relatif terhadap titik tertentu adalah besaran vektor, dan secara vektor ditulis:
L = R ´ P = m (R ´ v)
Bila diturunkan, menjadi:
karena t = F ´ R
maka t =
Apabila suatu sistem mula-mula mempunyai memontum sudut total SL, dan sistem mempunyai momentum sudut total akhir SL’, setelah beberapa waktu, maka berlaku hukum kekekalan momentum sudut. Perhatikan seorang penari balet yang menari sambil berputar dalam dua keadaan yang berbeda.
Pada keadaan pertama, penari merentangkan tangan mengalami putaran yang lambat, sedangkan pada keadaan kedua, penari bersedekap tangan roknya berkibar-kibar dengan putaran yang cepat. Momentum sudut total awal = momentul sudut total akhir
SL = SL’
L1 + L2 = L1’ + L2’
Hukum Kekekalan momentum rotasi sebagai berikut. I1 ω1 + I2 ω2 = I1’ ω1’+ I2’ ω2’
Simak Juga : Kesetimbangan Benda Tegar – Pengertian, Sifat, Jenis dan Contohnya
Energi Kinetik Rotasi
Misalkan sebuah sistem terdiri atas dua partikel yang massanya m1 dan m2 dan rotasi bergerak dengan kecepatan linier v1 dan v2, maka energi kinetik partikel ke 1 adalah ½ m1v12. Oleh karena itu, energi kinetik sistem dua partikel itu adalah (energi kinetik partikelke 2 adalah ½ m2v22 ) :
EK = ½ m1 v12 + ½ m2v22
Dalam sistem benda tegar energi kinetiknya:
EK = S ½ mi vi2
Benda tegar yang berotasi terhadap suatu sumbu dengan kecepatan sudut w, kecepatan tiap partikel adalah vi = ω . Ri , di mana Ri adalah jarak partikel ke sumbu rotasi.
jadi EK =S ½ mivi2
= S ½ mi Ri2 ω2
= ½ (S mi Ri2) ω2
EK = ½ I . ω2
karena L = I . ω
maka EK = ½ L . ω
atau EK = ½
Masalah umum di mana benda tegar berotasi terhadap sebuah sumbu yang melalui pusat massanya dan pada saat yang sama bergerak translasi relatif terhadap seorang pengamat. Karena itu, energi kinetik total benda dapat dituliskan sebagai berikut.
EK = ½ mv2 + ½ I . ω2
Dalam hal ini hukum kekekalan energi total atau energi mekanik adalah:
E = EK + EP = konstan
½ mv2 + ½ I ω2 + mgh = konstan
Sudah selesai membaca materi ini ? Ayo lihat dulu Daftar Materi Fisika



