Contoh Soal Dinamika Rotasi dan Keseimbangan Benda Tegar – Rotasi adalah perputaran benda pada suatu sumbu yang tetap, misalnya perputaran gasing dan perputaran bumi pada poros/sumbunya. Untuk bumi, rotasi ini terjadi pada garis/poros/sumbu utara-selatan. Keseimbangan benda tegar merupakan kondisi dimana momentum benda tegar sama dengan nol. Sedangkan benda tegar sendiri adalah benda yang bentuknya (geometrinya) akan selalu tetap sekalipun dikenakan gaya. Jadi sekalipun dia bergerak translasi atau rotasi bentuknya tidak akan berubah, contohnya meja, kursi, bola, dll.
Kali ini Soalkimia.com akan membagikan Contoh Soal dan Penyelesaian Dinamika Rotasi dari berbagai penerbit buku fisika untuk kamu pelajari sebagai persiapan ulangan harian (UH) ataupun Ujian Nasional.
1 – 10 Soal Dinamika Rotasi dan Pembahasan
1. Besaran yang dapat menyebabkan benda bergerak secara rotasi adalah…
a. momentum sudut
b. pecepatan sudut
c. momen gaya
d. momen inersia
e. gaya sentripetal
Jawaban : C
Pembahasan :
Benda dapat berotasi bila dikenai torsi atau momen gaya. Momen gaya itu
sendiri merupakan besaran yang dipengaruhi oleh gaya dan lengan, jadi hal tersebutlah yang dapat menyebabkan berda mengalami rotasi.
2. Bentuk lintasan dari gerak rotasi adalah…
a. lurus
b. melingkar
c. bergerigi
d. miring
e. horizontal
Jawaban : B
Pembahasan :
Bentuk lintasan dari gerak rotasi yaitu berbentuk lingkaran
3. Berikut yang merupakan symbol dari momen inersia adalah…
a. L
b. A
c. F
d. i
e. I
Jawaban : E
Pembahasan :
Momen inersia disimbolkan dengan I. Dengan persamaan I= Mr²
Dengan
I= momen inersia (Kg.m²)
m= massa partikel (Kg)
R= Jari- jari rotasi (m)
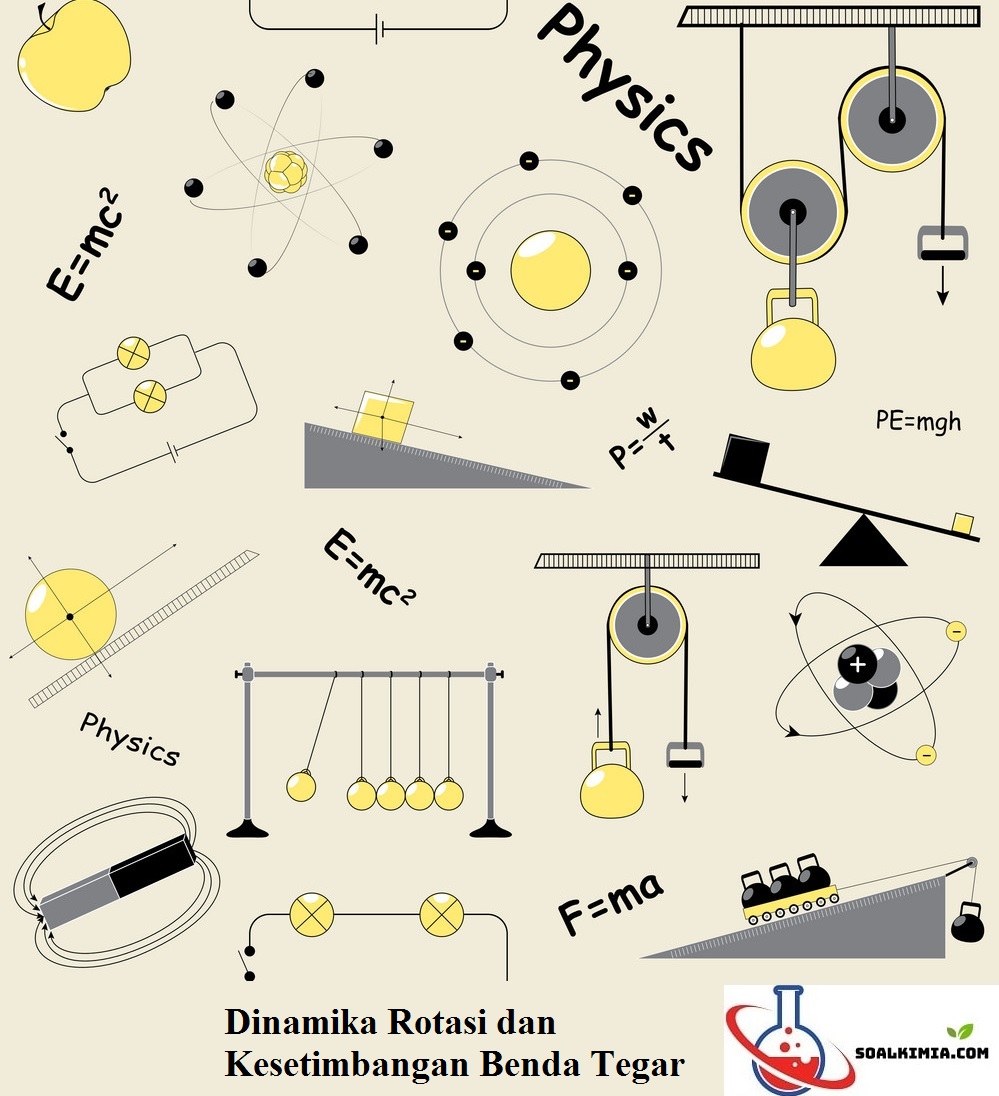
4. Perhatikan gambar lengan dari orang yang mencoba memutar baut
menggunakan kunci pas di bawah ini!
Berdasarkan gambar di atas, pernyataan manakah yang menghasilkan momen gaya paling besar?
a. besar f = 25 n bekerja tegak lurus batang berjarak 0,75 m dari baut
b. besar f = 50 n bekerja membentuk sudut 30° dengan kunci pas berjarak 0,75 m dari baut
c. besar f = 30n bekerja tegak lurus batang berjarak 1,0m dari baut
d.besar f = 75 n bekerja sejajar dengan panjang kunci pas berjarak 0,50m dari baut
e. besar f = 100n bekerja membentuk sudut 150° dengan kunci pas berjarak 0,50 m dari baut
Jawaban : A
Pembahasan :
Gambar di atas, pernyataan yang menghasilkan momen gaya paling besar
besar f = 25 n bekerja tegak lurus batang berjarak 0,75 m dari baut
5. Momen gaya menghasilkan nilai maksimum saat…
a. membentuk sudut 0°
b. saling berlawanan arah
c. tegak lurus antara F dengan r
d. putarannya searah jarum jam
e. putarannya berlawanan arah jarum jam
Jawaban : C
Pembahasan :
Momen gaya selalu membentuk sudut 90 derajat, momen gaya bernilai
maksimum ketika tegak lurus antara F dan r
Simak Juga : Contoh Soal Hukum Newton Pilihan Ganda
6. Katrol cakram pejal bermassa 1 kg dan berjari-jari 10 cm, pada tepinya dililitkan tali, salah satu ujung tali digantungi beban 1 kg. Anggap tali tak bermassa. Percepatan gerak turunnya beban adalah… (g=10m/s²)
a. 10 m/s²
b. 12 m/s²
c.15 m/s²
d. 20 m/s²
e. 22 m/s²
Jawaban : D
Pembahasan :
Diketahui :
F = w = m g = (1)(10) = 10 Newton
r = 0,1 meter
Ditanya : percepatan beban (a) ?
Jawaban :
Hitung momen inersia dan momen gaya :
Momen inersia katrol cakram pejal :
I = ½ m r²
= ½ (1)(0,1)²
= (0,5)(0,01) = 0,005 kg m²
7. Sebuah pesawat terbang dapat mengangkasa karena…..
a. perbedaan tekanan dari aliran- aliran udara
b. pengaturan titik berat pesawat
c. gaya angkat dari mesin pesawat
d. perubahan momentum dari pesawat
e. berat pesawat yang lebih kecil daripada berat udara yang dipindahkan
Jawaban : A
Pembahasan :
Pesawat terbang dapat mengangkasa karena kelajuan udara yang melalui sayap pesawat, adanya perbedaan tekanan udara yang melalui sayap pesawat yang menyebabkan pesawat dapat terangkat dan mengudara
8. Berikut yang merupakan simbol dari torsi adalah…
a. τ
b. µ
c. ω
d. α
e. θ
Jawaban : A
Pembahasan :
Torsi disimbolkan dengan τ. Dengan persamaan τ= r x F
Dengan τ= torsi
r= lengan momen
F= gaya
9. Momen gaya disebut juga dengan…
a. pusat gaya
b. torsi
c. momentum
d. kecepatan sudut
e. percepatan sudut
Jawaban : B
Pembahasan :
Benda dapat berotasi bila dikenai torsi atau momen gaya
10. Dibawah ini yang merupakan contoh penerapan dinamika rotasi dalam kehidupan sehari- hari adalah…
a. penembak
b. pemanah
c. penari balet
d. peselancar
e. pelari
Jawaban : C
Pembahasan :
Penari balet contoh penerapan dari dinamika rotasi karena ada unsur perputaran didalamnya, saat ingin melakukan perputaran penari balet terkadang melipat dan merentangkan tangannya untuk menambah kecepatan.
11 – 20 Soal Dinamika Rotasi dan Pembahasan
11. Soal Tentang Momentum Sudut
Seorang anak dengan kedua lengan berada dalam pangkuan sedang berputar pada suatu kursi putar dengan 1,00 putaran/s.
Ketika ia merentangkan kedua lengannya, ia diperlambat sampai 0,40 putaran/s. Tentukan perbandingan:
a. momen inersia gabungan anak + kursi sebelum dan sesudah kedua lengannya direntangkan
b. energi kinetik sebelum dan sesudahnya
Cara Penyelesaian:
ω₁= 1 rps (sebelum merentangkan tangan)
ω₂= 0,4 rps (sesudah merentangkan tangan)
(a) Gunakan Hukum Kekekalan momentum sudut
L₁= L₂
I₁ω₁= I₂ω₂
=>I₁(1) = I₂(0,4)
maka : I₁: I₂= 0,4 : 1
atau : I₁: I₂= 2 : 5
(b) Rumus energi kinetik rotasi adalah : Ekr = ½ I ω²
Maka :
Ekr₁= ½ I₁ω₁² dan Ekr₂= ½ I₂ω₂²
Sehingga perbandingan :
Ekr₁: Ekr₂= (I₁/ I₂).(ω₁: ω₂)²
Ekr₁: Ekr₂= (2/5) . (5/2)² = 5/2
Ekr₁: Ekr₂= 5 : 2
12. Soal Tentang Momen Inersia
Sebuah roda bermassa 6 kg dengan radius girasi 40 cm, berputar dengan kecepatan 300 rpm. Tentukan momen inersia dan energi kinetik rotasi roda itu.
Cara Penyelesaian :
I = M k2 = (6 kg) (0,40 m)2 = 0,96 kg . m2
Ekr = ½ I ω2 ; dengan ω harus dinyatakan dalam rad/s.
ω harus dinyatakan dalam rad/s.
ω = (300 putaran / menit) (1 menit / 60 sekon) (2 π rad / 1 putaran) = 31,4 rad/s
maka Ekr = ½ I ω2 = ½ (0,96 kg . m2) (31,4 rad/s)2 = 473 J.
13. Tentang Momentum Sudut
Sebuah bola pejal 500g berjari – jari 7 cm dengan momen kelembaman (inersia) sebesar 0,00098 kg . m2, berputar dengan 30 putaran/detik (put/s) pada sebuah sumbu yang melalui titik pusatnya. Berapakah
a. energi kinetik rotasi
b. momentum sudut.
(Catatan : ω harus dalam rad/s).
Penyelesaian :
(a) Dengan mengetahui bahwa ω = 30 put/s = 188 rad/s, maka akan kita peroleh :
Ekr = ½ I ω2 = ½ (0,00098 kg . m2) (188 rad/s)2 = 17,3 J
(b) Momentum sudutnya :
L = I ω = (0,00098 kg . m2) (188 rad/ s) = 0,184 kg . m2/s
14. Soal Tentang Hubungan antara Momen gaya dan percepatan sudut
Baling – baling suatu pesawat bermassa 70 kg dengan radius girasi 75 cm. Berapakah momen inersia baling – baling itu?
Agar baling – baling dapat dipercepat dengan percepatan sudut sebesar 4 put/s2, berapakah torsi yang diperlukan?
M = 70 kg ; k = 75 cm = 0,75 m ; I = ….? dan τ = ….?
Pembahasan :
I = Mk2 = (70 kg) (0,75 m)2 = 39 kg . m2
Dengan menggunakan τ = I α, dan α harus dalam rad/s2
α = (4 put / s2) (2 π rad/putaran) = 8 π rad/s2
Maka,
τ = I α = (39 kg . m2) (8 π rad/s2) = 990 N . m
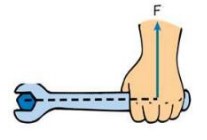
15. Momen gaya (torsi)
Pada gambar menunjukkan gaya 40 N yang dikerjakan secara tangensial pada tepi roda berjari – jari 20 cm, dan ber-momen inersia 30 kg . m2. Tentukan momen gaya τ = ..? yang dimiliki benda tersebut.
r = 20 cm = 0,2 m
F = 40 N
Penyelesaian :
16. Usaha dan Usaha dalam Gerak Rotasi
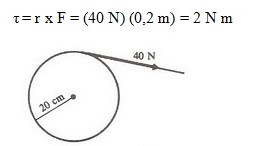
Sebuah silinder pejal menggelinding menaiki suatu bidang miring seperti pada gambar. Kecepatan awal silinder saat akan menaiki bidang miring adalah 20 m/s.
Bila energi yang hilang akibat gesekan dapat diabaikan, ternyata silinder mampu mencapai ketinggian h sebelum berbalik arah. Berapakah tinggi h ? (Silinder pejal, I = ½ mR2)
Penyelesaian :
17. Usaha dalam Gerak Rotasi
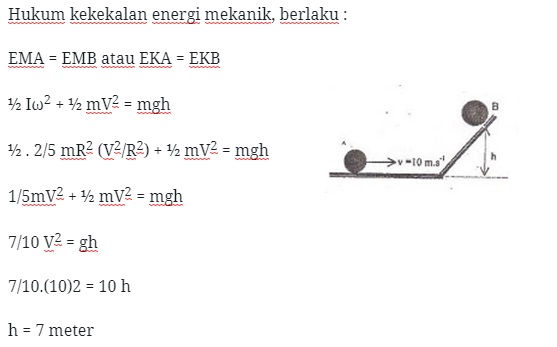
Sebuah pejal homogen menggelinding pada bidang datar dengan kecepatan v = 10 m/s. Bola kemudian menggelinding ke atas menurut bidang miring hingga menc apai titik balik B setinggi h.
Jika percepatan gravitasi g = 10 m/s, maka h = ? (benda berbentuk bola pejal maka : I = 2/5mR2 dan ω = V/R)
Penyelesaian :
Lihat Juga : Contoh Soal Virus Biologi Pilihan Ganda [+Kunci Jawaban]
18. Hubungan antara Momen gaya dan percepatan sudut
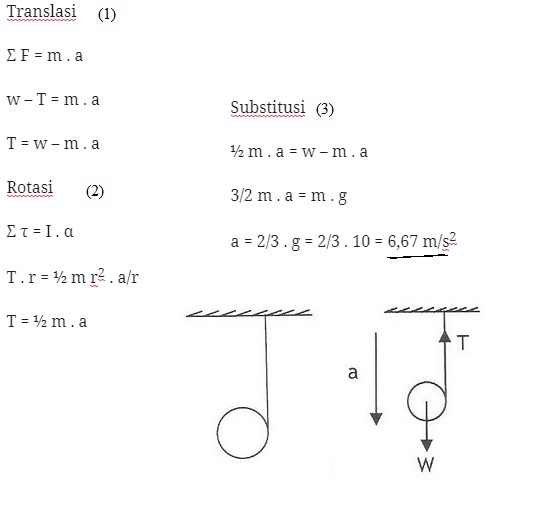
Sebuah yoyo bermassa 500 gram melakukan gerak seperti pada gambar. Berapa percepatan yang dialami?
Penyelesaian :
Kita Umpakan yoyo tersebut adalah silinder pejal
19. Momen Inersia
Sebuah partikel bermassa 2 kg diikatkan pada seutas tali yang panjangnya 0,5 meter. Berapa momen Inersia partikel tersebut jika diputar ?
Cara Penyelesaian :
(Dalam soal ini kita membahas tentang rotasi partikel, bukan benda tegar. Jadi bisa dianggap massa benda terkonsentrasi pada pusat massanya)
Momen inersianya :
I = mr2
I = (2 kg) (0,5m)2
I = 0,5 kg m2
20. Momen gaya (torsi)
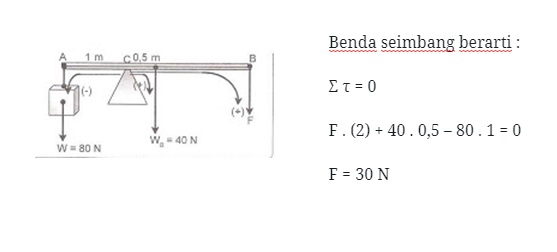
Batang AB yang massanya 4 kg dan panjang 3 m diberi penopang pada jarak 1 m dari ujung A. Pada ujung A diberi beban 80 N.
Agar batang seimbang, maka di ujung B harus diberi gaya sebesar ?
Penyelesaian :
Wbatang = 4 . 10 = 40 N (di tengah – tengah)
Jadi gaya – gaya yang bekerja terlihat seperti pada gambar berikut
Download soal Dinamika rotasi dan Kesetimbangan benda tegar
Penting : Kami menyarankan untuk mendownload File dalam format .doc atau .pdf melalui link dibawah ini agar mudah dibaca apabila beberapa equation diwebsite kurang jelas.
Sudah selesai membaca dan berlatih soal ini ? Ayo lihat dulu Daftar Soal Fisika





Terima kasih sangat membantu semoga menjadi ladang amal
Cara download nya gmn min
https://drive.google.com/file/d/1k9IuOKmAT9BWOx5yU90LyqzNbJwDDtYi/view