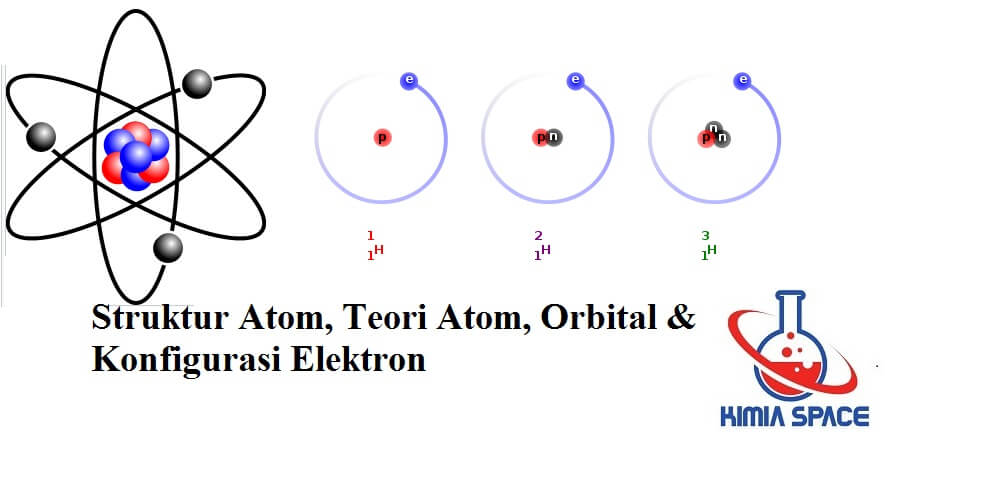
Struktur Atom (Atomic Structure) adalah teori terhadap nukleus, di pusat atom, terdiri dari proton dan neutron. Mengorbit di sekitar nukleus adalah elektron.
Hukum-hukum mekanika klasik seperti Hukum Newton dapat menjelaskan materi berukuran makro dengan akurat. Akan tetapi, hukum tersebut tidak mampu menjelaskan gejala yang ditimbulkan oleh materi berukuran mikro, seperti elektron, atom, atau molekul. Materi berukuran mikro hanya dapat dijelaskan dengan teori mekanika kuantum.
Teori atom berdasarkan mekanika kuantum dirumuskan oleh Werner Heisenberg dan Erwin Schrodinger. Selain itu, sumbangan pemikiran terhadap teori ini diberikan juga oleh Paul Dirac, Max Born, dan Pauli.
Keunggulan teori atom mekanika kuantum dapat menjelaskan materi berskala mikro seperti elektron dalam atom sehingga penyusunan (keberadaan) elektron dalam atom dapat digambarkan melalui penulisan konfigurasi elektron dan diagram orbital. Bagaimanakah menuliskan konfigurasi elektron dan diagram orbital? Simak Materi berikut ini.
Simak Juga : Soal Struktur Atom
A. Teori Atom Modern
Teori atom Bohr cukup berhasil dalam menjelaskan gejala spektrum atom hidrogen, bahkan dapat menentukan jari-jari atom hidrogen dan tingkat energi atom hidrogen pada keadaan dasar berdasarkan postulat momentum sudut elektron.
Seiring dengan perkembangan ilmu pengetahuan, ditemukan fakta-fakta baru yang menunjukkan adanya kelemahan pada teori atom Bohr. Oleh karena itu, dikembangkan teori atom mekanika kuantum
Teori Atom Bohr
Sebagaimana telah Anda ketahui, teori atom Bohr didasarkan pada empat postulat sebagai berikut.
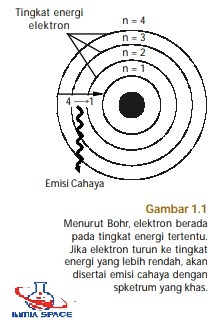
- Elektron-elektron dalam mengelilingi inti atom berada pada tingkattingkat energi atau orbit tertentu. Tingkat-tingkat energi ini dilambangkan dengan n=1, n=2, n=3, dan seterusnya. Bilangan bulat ini dinamakan bilangan kuantum (perhatikan Gambar 1.1).
- Selama elektron berada pada tingkat energi tertentu, misalnya n=1, energi elektron tetap. Artinya, tidak ada energi yang diemisikan (dipancarkan) maupun diserap.
- Elektron dapat beralih dari satu tingkat energi ke tingkat energi lain disertai perubahan energi. Besarnya perubahan energi sesuai dengan persamaan Planck, E=hv.
- Tingkat energi elektron yang dibolehkan memiliki momentum sudut tertentu. Besar momentum sudut ini merupakan kelipatan dari h/2p atau nh/2p, n adalah bilangan kuantum dan h tetapan Planck.
a. Peralihan Antartingkat Energi
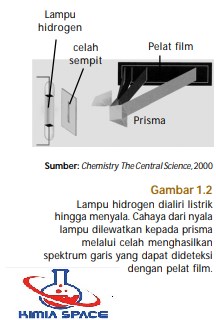
Model atom Bohr dapat menerangkan spektrum atom hidrogen secara memuaskan. Menurut Bohr, cahaya akan diserap atau diemisikan dengan frekuensi tertentu (sesuai persamaan Planck) melalui peralihan elektron dari satu tingkat energi ke tingkat energi yang lain. Jika atom hidrogen menyerap energi dalam bentuk cahaya maka elektron akan beralih ke tingkat energi yang lebih tinggi.
Sebaliknya, jika atom hidrogen mengemisikan cahaya maka elektron akan beralih ke tingkat energi yang lebih rendah. Pada keadaan stabil, atom hidrogen memiliki energi terendah, yakni elektron berada pada tingkat energi dasar (n=1). Jika elektron menghuni n>1, dinamakan keadaan tereksitasi. Keadaan tereksitasi ini tidak stabil dan terjadi jika atom hidrogen menyerap sejumlah energi.
Atom hidrogen pada keadaan tereksitasi tidak stabil sehingga energi yang diserap akan diemisikan kembali menghasilkan garis-garis spektrum (perhatikan Gambar 1.2). Kemudian, elektron akan turun ke tingkat energi yang lebih rendah. Nilai energi yang diserap atau diemisikan dalam
transisi elektron bergantung pada transisi antartingkat energi elektron.
Persamaannya dirumuskan sebagai berikut :
b. Kelemahan Model Atom Bohr
Gagasan Bohr tentang pergerakan elektron mengitari inti atom seperti sistem tata surya membuat teori atom Bohr mudah dipahami dan dapat diterima pada waktu itu. Akan tetapi, teori atom Bohr memiliki beberapa kelemahan, di antaranya sebagai berikut.
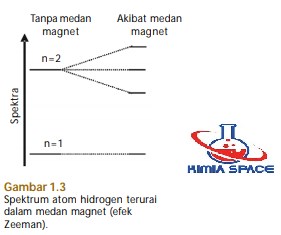
- Jika atom ditempatkan dalam medan magnet maka akan terbentuk spektrum emisi yang rumit. Gejala ini disebut efek Zeeman (perhatikan Gambar 1.3).
- Jika atom ditempatkan dalam medan listrik maka akan menghasilkan spektrum halus yang rumit. Gejala ini disebut efek Strack.
Pakar fisika Jerman, Sommerfeld menyarankan, disamping orbit berbentuk lingkaran juga harus mencakup orbit berbentuk elips. Hasilnya, efek Zeeman dapat dijelaskan dengan model tersebut, tetapi model atom Bohr-Sommerfeld tidak mampu menjelaskan spektrum dari atom berelektron banyak.
Sepuluh tahun setelah teori Bohr lahir, muncul gagasan de Broglie tentang dualisme materi, disusul Heisenberg tentang ketidakpastian posisi dan momentum partikel. Berdasarkan gagasan tersebut dan teori kuantum dari Planck, Schrodinger berhasil meletakkan dasar-dasar teori atom terkini, dinamakan teori atom mekanika kuantum.
Teori Atom Mekanika Kuantum
Kegagalan teori atom Bohr dalam menerangkan spektra atom hidrogen dalam medan magnet dan medan listrik, mendorong Erwin Schrodinger mengembangkan teori atom yang didasarkan pada prinsipprinsip mekanika kuantum.
Teori atom mekanika kuantum mirip dengan yang diajukan oleh model atom Bohr, yaitu atom memiliki inti bermuatan positif dikelilingi oleh elektron-elektron bermuatan negatif. Perbedaannya terletak pada posisi elektron dalam mengelilingi inti atom.
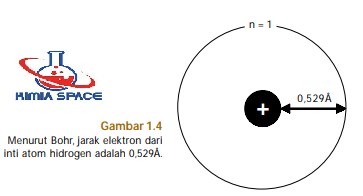
Menurut Bohr, keberadaan elektron-elektron dalam mengelilingi inti atom berada dalam orbit dengan jarak tertentu dari inti atom, yang disebut jari-jari atom (perhatikan Gambar 1.4).
Menurut teori atom mekanika kuantum, posisi elektron dalam mengelilingi inti atom tidak dapat diketahui secara pasti sesuai prinsip ketidakpastian Heisenberg. Oleh karena itu, kebolehjadian (peluang) terbesar ditemukannya elektron berada pada orbit atom tersebut. Dengan kata lain, orbital adalah daerah kebolehjadian terbesar ditemukannya elektron dalam atom.
Baca Juga : 25+ Soal Struktur Atom Pilihan Ganda Beserta Pembahasannya
Menurut model atom mekanika kuantum, gerakan elektron dalam mengelilingi inti atom memiliki sifat dualisme sebagaimana diajukan oleh de Broglie. Oleh karena gerakan elektron dalam mengelilingi inti memiliki sifat seperti gelombang maka persamaan gerak elektron dalam mengelilingi inti harus terkait dengan fungsi gelombang. Dengan kata lain, energi gerak (kinetik) elektron harus diungkapkan dalam bentuk persamaan fungsi gelombang.
Persamaan Schrodinger
Persamaan yang menyatakan gerakan elektron dalam mengelilingi inti atom dihubungkan dengan sifat dualisme materi yang diungkapkan dalam bentuk koordinat Cartesius.
Persamaan ini dikenal sebagai persamaan Schrodinger. Dari persamaan Schrodinger ini dihasilkan tiga bilangan kuantum, yaitu
- bilangan kuantum utama (n),
- bilangan kuantum azimut( A ),
- dan bilangan kuantum magnetik(m).
Ketiga bilangan kuantum ini merupakan bilangan bulat sederhana yang menunjukkan peluang adanya elektron di sekeliling inti atom. Penyelesaian persamaan Schrodinger menghasilkan tiga bilangan kuantum. Orbital diturunkan dari persamaan Schrodinger sehingga terdapat hubungan antara orbital dan ketiga bilangan kuantum tersebut.
a. Bilangan Kuantum Utama (n)
Bilangan kuantum utama (n) memiliki nilai n = 1, 2, 3, …, n. Bilangan kuantum ini menyatakan tingkat energi utama elektron dan sebagai ukuran kebolehjadian ditemukannya elektron dari inti atom. Jadi, bilangan kuantum utama serupa dengan tingkat-tingkat energi elektron atau orbit menurut teori atom Bohr. Bilangan kuantum utama merupakan fungsi jarak yang dihitung dari inti atom (sebagai titik nol). Jadi, semakin besar nilai n, semakin jauh jaraknya dari inti.
Oleh karena peluang menemukan elektron dinyatakan dengan orbital maka dapat dikatakan bahwa orbital berada dalam tingkat-tingkat energi sesuai dengan bilangan kuantum utama (n). Pada setiap tingkat energi terdapat satu atau lebih bentuk orbital. Semua bentuk orbital ini membentuk kulit (shell). Kulit adalah kumpulan bentuk orbital dalam bilangan kuantum utama yang sama.
Kulit-kulit ini diberi lambang mulai dari K, L, M, N, …, dan seterusnya. Hubungan bilangan kuantum utama dengan lambang kulit sebagai berikut.
b. Bilangan Kuantum Azimut ( A )
Bilangan kuantum azimut disebut juga bilangan kuantum momentum sudut, dilambangkan dengan A. Bilangan kuantum azimut menentukan bentuk orbital. Nilai bilangan kuantum azimut adalah A= n–1. Oleh karena nilai n merupakan bilangan bulat dan terkecil sama dengan satu maka harga A juga merupakan deret bilangan bulat 0, 1, 2, …, (n–1). Jadi, untuk n=1 hanya ada satu harga bilangan kuantum azimut, yaitu 0. Berarti, pada kulit K (n=1) hanya terdapat satu bentuk orbital. Untuk n=2 ada dua harga bilangan kuantum azimut, yaitu 0 dan 1. Artinya, pada kulit L (n=2) terdapat dua bentuk orbital, yaitu orbital yang memiliki nilai A=0 dan orbital yang memiliki nilai A=1
Pada pembahasan sebelumnya, dinyatakan bahwa bentuk-bentuk orbital yang memiliki bilangan kuantum utama sama membentuk kulit. Bentuk orbital dengan bilangan kuantum azimut sama dinamakan subkulit. Jadi, bilangan kuantum azimut dapat juga menunjukkan jumlah subkulit dalam setiap kulit. Masing-masing subkulit diberi lambang dengan s, p, d, f, …, dan seterusnya. Hubungan subkulit dengan lambangnya adalah sebagai berikut
c. Bilangan Kuantum Magnetik (m)
Bilangan kuantum magnetik disebut juga bilangan kuantum orientasi sebab bilangan kuantum ini menunjukkan orientasi (arah orbital) dalam ruang atau orientasi subkulit dalam kulit. Nilai bilangan kuantum magnetik berupa deret bilangan bulat dari –m melalui nol sampai +m. Untuk A=1, nilai m=0, ±l. Jadi, nilai bilangan kuantum magnetik untuk A=1 adalah –l melalui 0 sampai +l.
- Subkulit-s (A =0) memiliki harga m=0, artinya subkulit-s hanya memiliki satu buah orbital. Oleh karena m=0, orbital-s tidak memiliki orientasi dalam ruang sehingga bentuk orbital-s dikukuhkan berupa bola yang simetris.
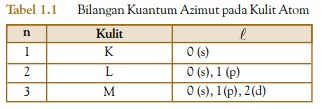
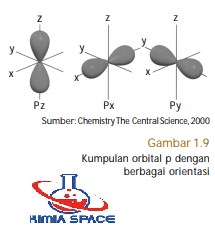
- Subkulit-p ( A=1) memiliki nilai m= –1, 0, +1. Artinya, subkulit-p memiliki tiga buah orientasi dalam ruang (3 orbital), yaitu orientasi pada sumbu-x dinamakan orbital px , orientasi pada sumbu-y dinamakan orbital py , dan orientasi pada sumbu-z dinamakan orbital pz .
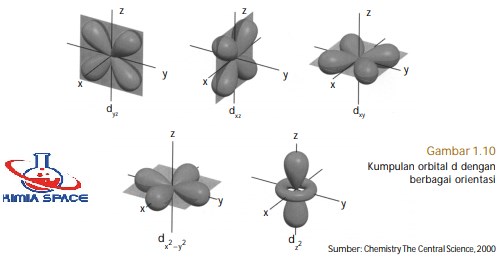
- Subkulit-d ( A=2) memiliki harga m= –2, –1, 0, +1, +2. Artinya, subkulit-d memiliki lima buah orientasi dalam ruang (5 orbital), yaitu pada bidang-xy dinamakan orbital dxy, pada bidang-xz dinamakan orbital dxz, pada bidang-yz dinamakan orbital dyz, pada sumbu x2 –y2 dinamakan orbital −2 2 dx y , dan orientasi pada sumbu z2 dinamakan orbital 2 dz .
Contoh orientasi orbital dapat dilihat pada Gambar 1.5
d. Bilangan Kuantum Spin (s)
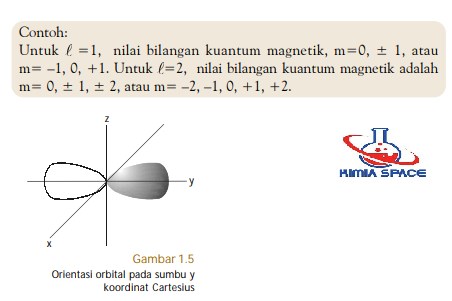
Di samping bilangan kuantum n, A , dan m, masih terdapat satu bilangan kuantum lain. Bilangan kuantum ini dinamakan bilangan kuantum spin, dilambangkan dengan s. Bilangan kuantum ini ditemukan dari hasil pengamatan radiasi uap perak yang dilewatkan melalui medan magnet, oleh Otto Stern dan W. Gerlach.
Pada medan magnet, berkas cahaya dari uap atom perak terurai menjadi dua berkas. Satu berkas membelok ke kutub utara magnet dan satu berkas lagi ke kutub selatan magnet (perhatikan Gambar 1.6). Berdasarkan pengamatan tersebut, disimpulkan bahwa atom-atom perak memiliki sifat magnet. Pengamatan terhadap atom-atom unsur lain, seperti atom Li, Na, Cu, dan Au selalu menghasilkan gejala yang serupa.
Atom-atom tersebut memiliki jumlah elektron ganjil. Munculnya sifat magnet dari berkas uap atom disebabkan oleh spin atau putaran elektron pada porosnya. Berdasarkan percobaan Stern-Gerlach, dapat disimpulkan bahwa ada dua macam spin elektron yang berlawanan arah dan saling meniadakan.
Pada atom yang jumlah elektronnya ganjil, terdapat sebuah elektron yang spinnya tidak ada yang meniadakan. Akibatnya, atom tersebut memiliki medan magnet.
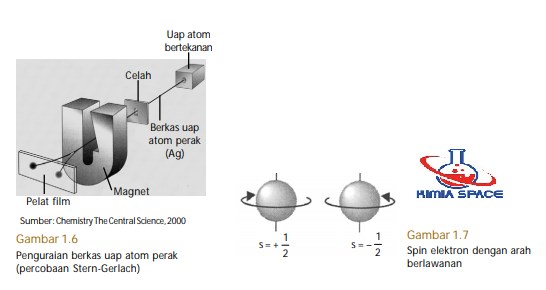
Spin elektron dinyatakan dengan bilangan kuantum spin. Bilangan kuantum ini memiliki dua harga yang berlawanan tanda, yaitu +½ dan –½ . Tanda (+) menunjukkan putaran searah jarum jam dan tanda (–) arah sebaliknya (perhatikan Gambar 1.7). Adapun harga ½ , menyatakan fraksi elektron.
B. Bentuk Orbital
Bentuk orbital ditentukan oleh bilangan kuantum azimut. Bilangan kuantum ini diperoleh dari suatu persamaan matematika yang mengandung trigonometri (sinus dan cosinus). Akibatnya, bentuk orbital ditentukan oleh bentuk trigonometri dalam ruang.
Orbital-s
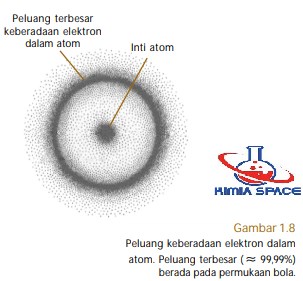
Orbital-s memiliki bilangan kuantum azimut, A= 0 dan m= 0. Oleh karena nilai m sesungguhnya suatu tetapan (tidak mengandung trigonometri) maka orbital-s tidak memiliki orientasi dalam ruang sehingga orbital-s ditetapkan berupa bola simetris di sekeliling inti.
Permukaan bola menyatakan peluang terbesar ditemukannya elektron dalam orbital-s. Hal ini bukan berarti semua elektron dalam orbital-s berada di permukaan bola, tetapi pada permukaan bola itu peluangnya tertinggi (≈ 99,99%), sisanya boleh jadi tersebar di dalam bola, lihat Gambar 1.8.
Orbital-p
Orbital-p memiliki bilangan kuantum azimut, A= 1 dan m= 0, ±l. Oleh karena itu, orbital-p memiliki tiga orientasi dalam ruang sesuai dengan bilangan kuantum magnetiknya. Oleh karena nilai m sesungguhnya mengandung sinus maka bentuk orbital-p menyerupai bentuk sinus dalam ruang, seperti ditunjukkan pada Gambar 1.9.
Ketiga orbital-p memiliki bentuk yang sama, tetapi berbeda dalam orientasinya. Orbital-px memiliki orientasi ruang pada sumbu-x, orbital-py memiliki orientasi pada sumbu-y, dan orbital-pz memiliki orientasi pada sumbu-z. Makna dari bentuk orbital-p adalah peluang terbesar ditemukannya elektron dalam ruang berada di sekitar sumbu x, y, dan z. Adapun pada bidang xy, xz, dan yz, peluangnya terkecil.
Orbital-d
Orbital-d memiliki bilangan kuantum azimut A = 2 dan m = 0, ±1, ±2. Akibatnya, terdapat lima orbital-d yang melibatkan sumbu dan bidang, sesuai dengan jumlah bilangan kuantum magnetiknya. Orbital-d terdiri atas orbital- 2 dz , orbital- xz d , orbital- xy d , orbital- yz d , dan orbital- −2 2 dx y (perhatikan Gambar 1.10).
Orbital dxy, dxz, dyz, dan −2 2 dx y memiliki bentuk yang sama, tetapi orientasi dalam ruang berbeda. Orientasi orbital-dxy berada dalam bidang xy, demikian juga orientasi orbital-orbital lainnya sesuai dengan tandanya. Orbital −2 2 dx y memiliki orientasi pada sumbu x dan sumbu y. Adapun orbital 2 dz memiliki bentuk berbeda dari keempat orbital yang lain.
Orientasi orbital ini berada pada sumbu z dan terdapat “donat” kecil pada bidang-xy. Makna dari orbital-d adalah, pada daerah-daerah sesuai tanda dalam orbital (xy, xz, yz, x2 –y2 , z2 ) menunjukkan peluang terbesar ditemukannya elektron, sedangkan pada simpul-simpul di luar bidang memiliki peluang paling kecil. Bentuk orbital-f dan yang lebih tinggi dapat dihitung secara matematika,
Baca Juga : 10+ Soal Menentukan Bentuk Molekul (PEB dan PEI) [+Pembahasan]
tetapi sukar untuk digambarkan atau diungkapkan kebolehjadiannya sebagaimana orbital-s, p, dan d. Kesimpulan umum dari hasil penyelesaian persamaan Schrodinger dapat dirangkum sebagai berikut :
C. Konfigurasi Elektron Atom Polielektron
Persamaan Schrodinger hanya dapat diterapkan secara eksak untuk atom berelektron tunggal seperti hidrogen, sedangkan pada atom berelektron banyak tidak dapat diselesaikan.
Kesulitan utama pada atom berelektron banyak adalah bertambahnya jumlah elektron sehingga menimbulkan tarikmenarik antara elektron-inti dan tolak-menolak antara elektron-elektron semakin rumit. Oleh karena itu, untuk atom berlektron banyak digunakan metode pendekatan berdasarkan hasil penelitian dan teori para ahli.
Tingkat Energi Orbital
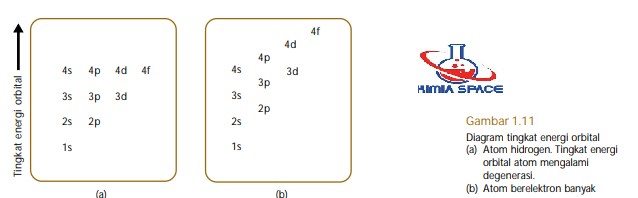
Pada atom berelektron banyak, setiap orbital ditandai oleh bilangan kuantum n, A, m, dan s. Bilangan kuantum ini memiliki arti sama dengan yang dibahas sebelumnya. Perbedaannya terletak pada jarak orbital dari inti. Pada atom hidrogen, setiap orbital dengan nilai bilangan kuantum utama sama memiliki tingkat-tingkat energi sama atau terdegenerasi. Misalnya, orbital 2s dan 2p memiliki tingkat energi yang sama. Demikian pula untuk orbital 3s, 3p, dan 3d.
Pada atom berelektron banyak, orbital-orbital dengan nilai bilangan kuantum utama sama memiliki tingkat energi yang sedikit berbeda. Misalnya, orbital 2s dan 2p memiliki tingkat energi berbeda, yaitu energi orbital 2p lebih tinggi. Perbedaan tingkat energi elektron pada atom hidrogen dan atom berelektron banyak ditunjukkan pada Gambar 1.11.
Perbedaan tingkat energi ini disebabkan oleh elektron yang berada pada kulit dalam menghalangi elektron-elektron pada kulit bagian luar. Sebagai contoh, elektron pada orbital 1s akan tolak-menolak dengan elektron pada orbital-2s dan 2p sehingga orbital-2s dan 2p tidak lagi sejajar (terdegenerasi) seperti pada atom hidrogen.
Hal ini menyebabkan elektron-elektron dalam orbital-2s memiliki peluang lebih besar ditemukan di dekat inti daripada orbital-2p (orbital-2s lebih dekat dengan inti).
Distribusi Elektron dalam Atom
Kulit terdiri atas subkulit yang berisi orbital-orbital dengan bilangan kuantum utama yang sama. Jumlah orbital dalam setiap kulit dinyatakan dengan rumus n2 dan jumlah maksimum elektron yang dapat menempati setiap kulit dinyatakan dengan rumus 2n²
Subkulit terdiri atas orbital-orbital yang memiliki bilangan kuantum azimut yang sama. Jumlah orbital, dalam setiap subkulit dinyatakan dengan rumus (2 A + 1). Oleh karena setiap orbital maksimum dihuni oleh dua elektron maka jumlah elektron dalam setiap subkulit dinyatakan dengan rumus 2(2 A + 1).
Aturan dalam Konfigurasi Elektron
Penulisan konfigurasi elektron untuk atom berelektron banyak didasarkan pada aturan aufbau, aturan Hund, dan prinsip larangan Pauli. Untuk menentukan jumlah elektron dalam atom, perlu diketahui nomor atom unsur bersangkutan.
a. Aturan Membangun (Aufbau)
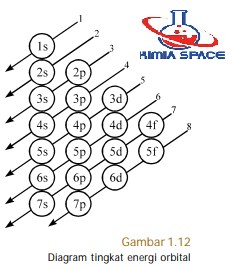
Aturan pengisian elektron ke dalam orbital-orbital dikenal dengan prinsip Aufbau (bahasa Jerman, artinya membangun). Menurut aturan ini, elektron dalam atom harus memiliki energi terendah, artinya elektron harus terlebih dahulu menghuni orbital dengan energi terendah (lihat diagram tingkat energi orbital pada Gambar 1.12).
Tingkat energi elektron ditentukan oleh bilangan kuantum utama. Bilangan kuantum utama dengan n = 1 merupakan tingkat energi paling rendah, kemudian meningkat ke tingkat energi yang lebih tinggi, yaitu n = 2, n = 3, dan seterusnya. Jadi, urutan kenaikan tingkat energi elektron adalah (n = 1) < (n = 2) < (n =3) < … < (n = n).
Setelah tingkat energi elektron diurutkan berdasarkan bilangan kuantum utama, kemudian diurutkan lagi berdasarkan bilangan kuantum azimut sebab orbital-orbital dalam atom berelektron banyak tidak terdegenerasi. Berdasarkan bilangan kuantum azimut, tingkat energi terendah adalah orbital dengan bilangan kuantum azimut terkecil atau A= 0. Jadi, urutan tingkat energinya adalah s < p < d < f < [ A = (n–1)].
Terdapat aturan tambahan, yaitu aturan (n+ A). Menurut aturan ini, untuk nilai (n+ A) sama, orbital yang memiliki energi lebih rendah adalah orbital dengan bilangan kuantum utama lebih kecil,
contoh:
2p (2+1 = 3) < 3s (3+0 =3), 3p (3+1 = 4) < 4s (4+0 =4), dan seterusnya.
Jika nilai (n+ A) berbeda maka orbital yang memiliki energi lebih rendah adalah orbital dengan jumlah (n+ A) lebih kecil,
contoh:
4s (4+0 = 4) < 3d (3+2 =5).
Dengan mengacu pada aturan aufbau maka urutan kenaikan tingkat energi elektron-elektron dalam orbital adalah sebagai berikut.
1s < 2s < 2p < 3s < 3p < 4s < 3d < 4p < 5s < 4d < 5p < 6s < 4f < …
b. Aturan Hund
Aturan Hund disusun berdasarkan data spektroskopi atom. Aturan ini menyatakan sebagai berikut.
- Pengisian elektron ke dalam orbital-orbital yang tingkat energinya sama, misalnya ketiga orbital-p atau kelima orbital-d. Oleh karena itu, elektron-elektron tidak berpasangan sebelum semua orbital dihuni.
- Elektron-elektron yang menghuni orbital-orbital dengan tingkat energi sama, misalnya orbital pz , px , py . Oleh karena itu, energi paling rendah dicapai jika spin elektron searah.
c. Prinsip Larangan Pauli
Menurut Wolfgang Pauli, elektron-elektron tidak boleh memiliki empat bilangan kuantum yang sama. Aturan ini disebut Prinsip larangan Pauli. Makna dari larangan Pauli adalah jika elektron-elektron memiliki ketiga bilangan kuantum (n, A, m) sama
maka elektron-elektron tersebut tidak boleh berada dalam orbital yang sama pada waktu bersamaan. Akibatnya, setiap orbital hanya dapat dihuni maksimum dua elektron dan arah spinnya harus berlawanan.
Sebagai konsekuensi dari larangan Pauli maka jumlah elektron yang dapat menghuni subkulit s, p, d, f, …, dan seterusnya berturut-turut adalah 2, 6, 10, 14, …, dan seterusnya. Hal ini sesuai dengan rumus: 2(2 A + 1)
Penulisan Konfigurasi Elektron
Untuk menuliskan konfigurasi elektron, bayangkan bahwa inti atom memiliki tingkat-tingkat energi, dan setiap tingkat energi memiliki orbitalorbital yang masih kosong. Kemudian, elektron-elektron ditempatkan pada orbital-orbital sesuai dengan urutan tingkat energinya (aturan Aufbau), dan tingkat energi paling rendah diisi terlebih dahulu.
Pengisian orbital dengan tingkat energi sama, seperti px , py , pz , diusahakan tidak berpasangan sesuai aturan Hund, tempatnya boleh di mana saja, px , py , atau pz . Jika setelah masing-masing orbital dihuni oleh satu elektron masih ada elektron lain maka elektron ditambahkan untuk membentuk pasangan dengan spin berlawanan.
Dalam setiap orbital maksimum dihuni oleh dua elektron, sesuai aturan Pauli (perhatikan Gambar 1.13). Penulisan konfigurasi elektron dapat diringkas sebab dalam kimia yang penting adalah konfigurasi elektron pada kulit terluar atau elektron valensi. Contoh konfigurasi elektron atom natrium dapat ditulis sebagai:
11Na: [Ne] 3s1 .
Lambang [Ne] menggantikan penulisan konfigurasi elektron bagian dalam
(10Ne: 1s2 2s2 2p6 ).
Sudah selesai membaca materi ini ? Ayo lihat dulu Daftar Materi Kimia