Vektor – Pengertian, Notasi, Ruang Lingkup, Sifat dan Operasi Hitungnya – Besaran Vektor dapat disajikan dengan menggunakan suatu bilangan real, kemudian diikuti dengan sistem suatu yang sesuai. Secara geometri, besaran vektor dapat disajikan dengan ruas garis berarah. Panjang ruas garis menyatakan panjang atau besar vaktor, sedangkan arah anak panah menunjukan arah vaktor.

Simak Juga : Contoh Soal Vektor dan Jawaban
A. Vektor dan Notasinya
Suatu vektor ialah suatu besaran yang mempunyai besar dan arah. Dengan demikian maka dua vektor yang mempunyai besar dan arah yang sama, maka dua vektor tersebut adalah sama, tanpa memandang di mana vektor tersebut berada.
Suatu vektor digambarkan dengan suatu anak panah di mana panjangnya anak panah menyatakan besarnya vektor dan arah anak panah menunjukkan arah dari vektor.
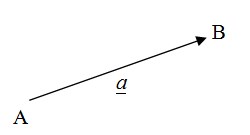
Gambar ini menunjukkan gambar vektor, A disebut titik tangkap vektor / titik pangkal vektor dan B disebut titik ujung vektor (terminal).
Vektor tersebut dinyatakan : ᾹB atau α.
Simak Juga : Besaran dan Satuan – Pengertian, Pengelompokan dan Contohnya
B. Vektor pada Bidang Datar R2 (Dimensi Dua)
Di dalam bidang datar (R2) suatu vektor yang titik pangkalnya di A (x1, y1) dan titik ujungnya di B (x2, y2) dapat dituliskan dalam bentuk komponen :

Vektor dalam bidang datar juga dapat dinyatakan dalam bentuk :
- Kombinasi linear vektor satuan i, j , misalnya vektor = xi + yj.
- Koordinat kartesius, yaitu : = (a1, a2).
- Koordinat kutub, yaitu :
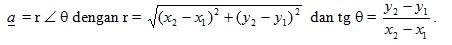
C. Ruang Lingkup Vektor
1. Kesamaan Dua Vektor
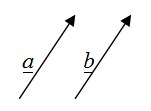
Dua buah vektor ḁ dan ḇ dikatakan sama apabila keduanya mempunyai besar (panjang) dan arah yang sama. Diperoleh: α = ḇ
2. Vektor Negatif
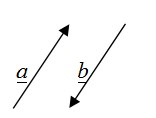
Vektor negatif dari α adalah vektor yang besarnya sama dengan vektor α tetapi arahnya berlawanan dan ditulis -α . Diperoleh: α = -ḇ.
3. Vektor Nol
Vektor nol adalah vektor yang besar / panjangnya nol dan arahnya tak tentu. Pada sistem koordinat kartesius vektor nol digambarkan berupa titik.
Di ruang dimensi dua vektor nol dilambangkan dengan :
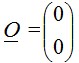
4. Vektor Posisi
Vektor posisi adalah vektor yang titik pangkalnya terletak pada pusat koordinat O(0,0) dan titik ujungnya berada pada koordinat lain. Vektor posisi pada R2 dari titik A(x,y) dinyatakan sebagai kombinasi linear vektor satuan sebagai berikut :
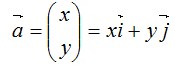
Penulisan vektor dan menyatakan vektor satuan pada sistem koordinat. Vektor satuan adalah vektor yang searah dengan sumbu X positif dan besarnya 1 satuan. Vektor satuan adalah vektor yang searah dengan sumbu Y positif dan besarnya 1 satuan.
5. Modulus atau Besar Vektor atau Panjang vektor
Misalnya
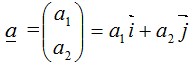
panjang vektor
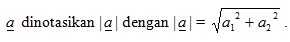
Jika diketahui titik A (x1, y1) dan B (x2, y2). Secara analitis, diperoleh komponen vektor
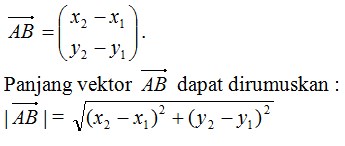
Contoh :
Diketahui titik A(3, -5) dan B(-2, 7), tentukan hasil operasi vektor tersebut !
- (a) Komponen vektor
- (b) Modulus/besar vektor
Jawab :
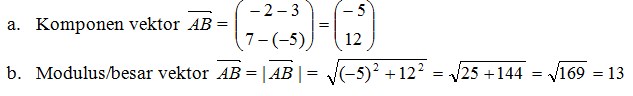
6. Vektor Satuan
Vektor satuan adalah vektor yang mempunyai panjang (besar) 1 satuan. Vektor satuan dapat ditentukan dengan cara membagi vektor tersebut dengan besar (panjang) vektor semula. Vektor satuan dari vektor dirumuskan:
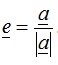
D. Operasi Hitung Vektor di R2
1. Operasi Penjumlahan Vektor
Penjumlahan dua vektor dapat dikerjakan dalam dua cara yaitu cara grafis dan analitis.
- Cara Grafis
1) Dengan cara penjumlahan segitiga atau segitiga vektor
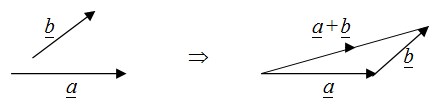
Cara: pangkal vektor ḇ digeser ke ujung vektor α maka vektor hasil α + ḇ adalah vektor yang menghubungkan pangkal vektor α dengan ujung vektor ḇ.
2) Dengan cara penjumlahan jajar genjang atau jajar genjang vektor
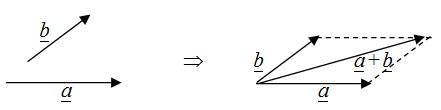
Cara: pangkal vektor ḇ digeser ke pangkal vektor α, dilukis jajar genjang, maka diagonal dari ujung persekutuan adalah α + ḇ.
Untuk melakukan penjumlahan lebih dari dua vektor digunakan aturan segi banyak (potongan).
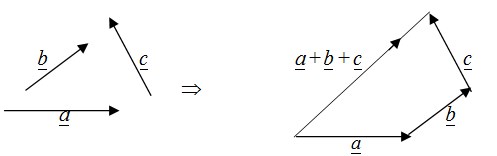
- Cara Analitis
1) Apabila kedua vektor diketahui mengapit sudut tertentu , maka dapat digunakan perhitungan dengan memakai rumus aturan cosinus seperti pada trigonometri.
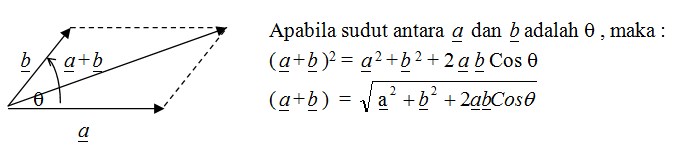
2) Jika vektor disajikan dalam bentuk komponen (dalam bidang kartesius) maka penjumlahan dapat dilakukan dengan menjumlahkan komponennya.
Misalnya:
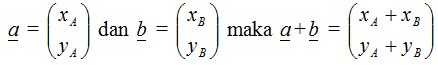
Contoh :

2) Operasi Pengurangan Vektor
Memperkurangkan vektor ḇ dari vektor α didefinisikan sebagai menjumlahkan vektor negatif ḇ pada vektor α dan ditulis :α – ḇ = α + (ḇ).
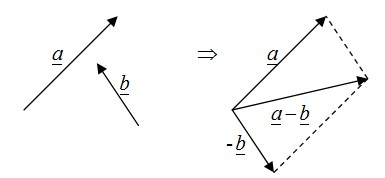
Apabila vektor disajikan dalam bentuk komponen (dalam bidang kartesius) maka pengurangan dapat dilakukan dengan mengurangkan komponen-komponennya.
3. Perkalian Vektor dengan Skalar
Jika α suatu vektor dan m adalah skalar (bilangan nyata), maka mα atau mα adalah suatu vektor dengan kemungkinan :
- Jika m > 0 maka mα adalah vektor yang besarnya m kali α dan searah dengan α.
- Jika m < 0 maka mα adalah vektor yang besarnya m kali α dan arahnya berlawanan dengan α.
- Jika m = 0 maka mα adalah nektor nol.
Contoh perkalian vektor dan skalar
- Vektor diberikan dalam bentuk gambar
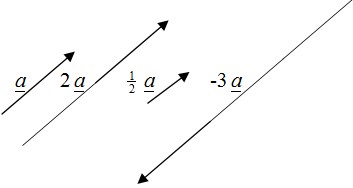
- Vektor diberikan dalam bentuk kpmponen
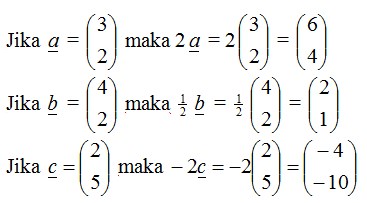
Apabila titik-titik dalam vektor dapat dinyatakan sebagai perkalian vektor yang lain, titik-titik itu disebut kolinier (segaris).
4. Perkalian dua vektor
Operasi perkalian pada vektor dapat dikerjakan melalui dua cara sebagai berikut :
Sudut antara kedua vektor diketahui
Diberikan vektor α =(a1, a2), ḇ = (b1, b2) dan sudut yang dibentuk oleh vektor α dan ḇ adalah ἀ. Perkalian antara vektor α dan ḇ dirumuskan sebagai berikut :
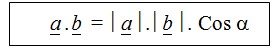
Contoh :
Tentukan hasil kali kedua vektor
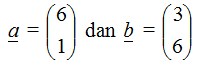
serta sudut antara kedua vektor adalah 60°!
Jawab:
Diketahui dua buah vektor sebagai berikut :

Sudut antara kedua vektor tidak diketahui
Diberikan vektor α = (a1, a2) dan ḇ = (b1, b2). Hasil kali kedua vektor dirumuskan sebagai berikut :
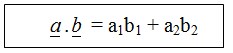
Contoh:
Diberikan vektor
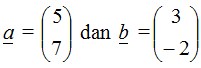
Tentukan hasil kali vektor α dan ḇ!
Jawab:
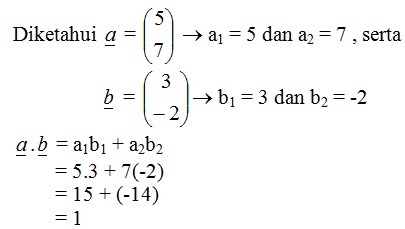
Jadi, hasil kali vektor α dan ḇ adalah 1.
Sementara itu, dari dua buah vektor pada sistem koordinat kartesius dapat kita cari besar sudut yang dibentuk oleh kedua vektor yang dirumuskan sebagai berikut :
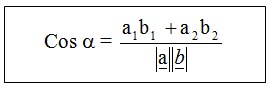
Sudah selesai membaca materi ini ? Ayo lihat dulu Daftar Materi Fisika



