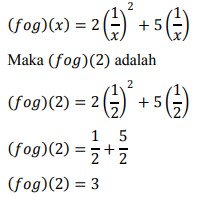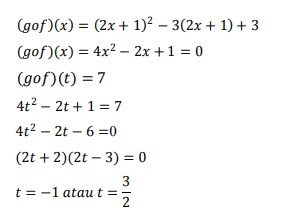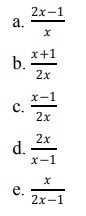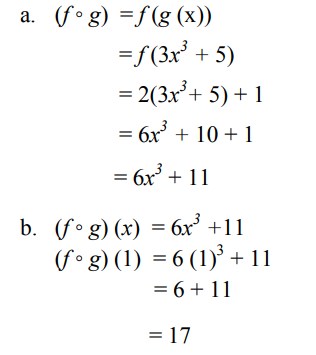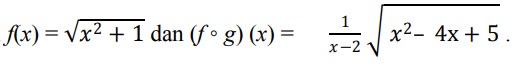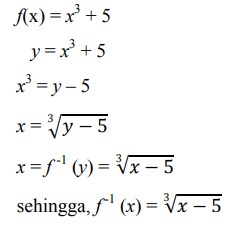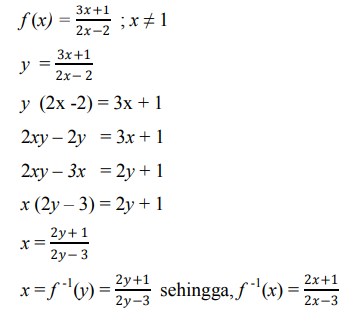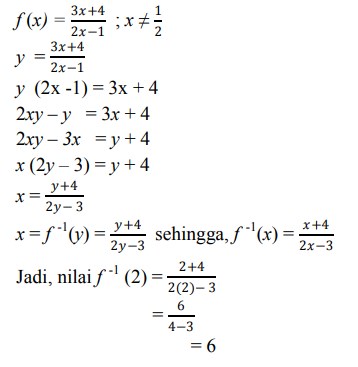Contoh Soal Fungsi Komposisi dan Jawaban

Contoh Soal Fungsi Komposisi dan Jawaban – Fungsi komposisi adalah penggabungan sebuah operasi dua jenis fungsi f(x) dan g(x) sehingga mampu menghasilkan sebuah fungsi baru.

Operasi fungsi komposisi tersebut biasa dilambangkan dengan “o” kemudian dapat dibaca komposisi ataupun bundaran. Fungsi baru inilah yang dapat terbentuk dari f(x) dan g(x) yaitu:

(f o g)(x) yang artinya g dimasukkan ke f
(g o f)(x) yang artinya f dimasukkan ke g

Fungsi tunggal adalah merupakan fungsi yang bisa dilambangkan dengan huruf “f o g” atau bisa dibaca “f bundaran g”.

Kemudian Fungsi (f o g) (x) = f (g (x)) → fungsi g (x) dikomposisikan sebagai fungsi f (x)

Sedangkan, “g o f” dibaca sebagai fungsi g bundaran f. Jadi, “g o f” adalah fungsi f diselesaikan dulu dari fungsi g.

Sifat yang terdapat pada fungsi komposisi adalah :

Jika f : A → B , g : B → C , h : C → D, maka berlaku :

(f o g)(x)≠(g o f)(x). Tidak berlaku sifat komutatif
[f o (g o h)(x)] = [(f o g ) o h (x)]. bersifat asosiatif
Jika fungsi identitas I(x), maka berlaku (f o l)(x) = (l o f)(x) = f(x)

1 – 10 Contoh Soal Fungsi Komposisi dan Jawaban

1. Jika f(x) = 2x² + 5x dan g(x) = 1/x maka (fog) (2) adalah …

a. 3

b. 2

c. 1

d. ½

e. 1/3

Jawaban : A

Pertama kita cari fungsi (f o g) (𝑥) dulu

2. Diketahui fungsi 𝑓(𝑥) = 2𝑥 + 1 dan 𝑔(𝑥) = 𝑥² − 3𝑥 + 3. Jika nilai (𝑔 o f) (𝑡) = 7 maka nilai t adalah …

a. 1 atau 2

b. -2/3 atau 1

c. -1 atau 2/3

d. -1 atau 3/2

e. -2 atau -1

Jawaban : D

Pertama kita hitung (𝑔 o f) (𝑥)

3. Diberikan dua buah fungsi masing-masing f(x) dan g(x) berturut-turut adalah sebagai berikut :

f(x) = 3x + 2

g(x) = 2 − x

Tentukan:

a) (f o g)(x)

b) (g o f)(x)

Pembahasan :

a) (f o g)(x)
“Masukkan g(x) nya ke f(x)” sehingga:
(f o g)(x) = f ( g(x) )
= f (2 − x)
= 3(2 − x) + 2
= 6 − 3x + 2
= − 3x + 8
b) (g o f)(x)
“Masukkan f (x) nya ke g (x)” sehingga:
(g o f)(x) = g ( f (x) )
= g ( 3x + 2)
= 2 − ( 3x + 2)
= 2 − 3x − 2
= − 3x

4. Diketahui 𝑓(𝑥) = 1 𝑥 dan 𝑔(𝑥) = 2𝑥 −1 maka nilai (𝑔‾¹𝑜𝑓‾¹)(𝑥) adalah …

Jawaban : B

Ada 2 cara untuk menyelesaikan soal tersebut, yaitu dengan menginvers masing-masing fungsi kemudian di komposisikan, atau menggunakan :
(𝑓𝑜 𝑔)−1(𝑥) = (𝑔‾¹𝑜𝑓‾¹)(𝑥)

5. Diberikan dua buah fungsi:

f(x) = 3x² + 4x + 1

g(x) = 6x

Tentukan:

a) (f o g)(x)

b) (f o g)(2)

Pembahasan :

Diketahui:
f(x) = 3x² + 4x + 1
g(x) = 6x
a) (f o g)(x)
= 3(6x)² + 4(6x) + 1
= 108x² + 24x + 1
= 18x² + 24x + 1
b) (f o g)(2)
(f o g)(x) = 108x² + 24x + 1
(f o g)(2) = 108(2)² + 24(2) + 1
(f o g)(2) = 432 + 48 + 1 = 481

Simak Juga : Soal Limit Fungsi Aljabar

6. Diketahui f(x) = x² + 1 dan g(x) = 2x − 3, maka (f o g)(x) = ….

A. 4x² − 12x + 10

B. 4x² + 12x + 10

C. 4x² − 12x − 10

D. 4x² + 12x − 10

E. − 4x² + 12x + 10

Jawaban : A

Pembahasan :

f(x) = x² + 1
g(x) = 2x − 3
(f o g)(x) =…….?
Masukkan g(x) nya ke f(x)
(f o g)(x) =(2x − 3)² + 1
(f o g)(x) = 4x² − 12x + 9 + 1
(f o g)(x) = 4x² − 12x + 10

7. Diketahui fungsi f(x) = 3x − 1 dan g(x) = 2x² + 3. Nilai dari komposisi fungsi (g o f)(1) =….

A. 7

B. 9

C. 11

D. 14

E. 17

Jawaban : C

Pembahasan :

Diketahui:
f(x) = 3x − 1 dan g(x) = 2x² + 3
(g o f)(1) =…….
Masukkan f(x) nya pada g(x) kemudian isi dengan 1
(g o f)(x) = 2(3x − 1)² + 3
(g o f)(x) = 2(9x² − 6x + 1) + 3
(g o f)(x) = 18x² − 12x + 2 + 3
(g o f)(x) = 18x² − 12x + 5
(g o f)(1) = 18(1)² − 12(1) + 5 = 11

8. Diberikan rumus komposisi dari dua fungsi :

(g o f)(x) = − 3x

dengan

g(x) = 2 − x

Tentukan rumus fungsi f(x) …

A. 3x + 1

B 3x – 2

C. 3x + ½

D. 3x – 1

E. 3x + 2

Jawaban : E

Pembahasan :

(g o f)(x) = − 3x
(g o f)(x) = g(f(x))
− 3x = 2 − (f(x))
− 3x = 2 − f(x)
f(x) = 2 + 3x
atau
f(x) = 3x + 2

9. Diberikan fungsi-fungsi sebagai berikut:

f(x) = 2 + x

g(x) = x² − 1

h(x) = 2x

Tentukan rumus dari (h o g o f)(x)…

A. x² – 4x + 3

B. x² – 4x – 3

C. x² + 4x + 3

D. x² + 4x – 3

E. x² + x + 3

Jawaban : C

Pembahasan :

Bisa dengan cara satu-satu dulu, mulai dari g bundaran f
(g o f)(x) = (2 + x)² − 1
= x² + 4x + 4 − 1
= x² + 4x + 3
Masukkan hasilnya ke fungsi h(x) sehingga didapatkan
(h o g o f)(x) = 2(x² + 4x + 3)
= 2x² + 8x + 6

10. Diketahui fungsi f(x) = x – 4 dan g(x) = x² – 3x + 10. Fungsi komposisi (gof)(x) =….

A. x² – 3x + 14

B. x² – 3x + 6

C. x² – 11x + 28

D. x² -11x + 30

E. x² -11x + 38

Jawaban : E

Pembahasan :

g (x) = x² – 3x + 10
(gof)(x) = (x – 4)² – 3 (x – 4) + 10
= x² – 8x + 16 – 3x + 12 + 10
= x² -11x + 38

11 – 15 Contoh Soal Fungsi Komposisi dan Jawaban

11. Fungsi f : R → R dan g : R → R ditentukan oleh f (x) = 2x + 1 dan g(x) = 3x³ + 5.

Tentukan :

a. (f ◦ g) (x)

b. (f ◦ g) (1)

Jawaban :

12. Jika g (x) = 3x – 2 dan (g ◦f) (x) = 3x² +1, maka tentukan f (x) !

Jawaban :

(g ◦ f) (x) = 3x² + 1 g
(f (x)) = 3x² + 1
3(f (x)) – 2 = 3x² + 1
3.f (x) = 3x² + 1
f (x) = x² + 1

13. Tentukanlah g(x-3), Jika diketahui

Jawaban :

14. Tentukan invers fungsi dari f (x) = x³ +5!

Jawaban :

15. Diketahui fungsi f : R → R dengan

Invers fungsi f adalah …..

Jawaban :

16. Nilai fungsi invers f(2) dari :

maka hasilnya adalah …

Jawaban :

Sudah selesai membaca dan berlatih Soal Fungsi Komposisi ini ? Ayo lihat dulu Soal Matematika lainnya

Contoh Soal Fungsi Komposisi dan Jawaban