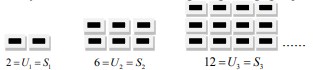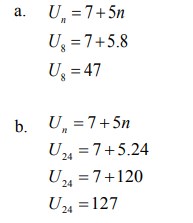Contoh Soal Pola Bilangan dan Jawaban [+Pembahasan] – Pola bilangan adalah susunan bilangan yang memiliki aturan atau pola tertentu.
Contoh :
- 1) 1, 2, 3, 4,5, ….mempunyai pola bilangan ditambah satu dari bilangansebelumnya, dimulai dari 1
- 2) 0, 2, 4, 6, 8, ….mempunyai pola bilangan ditambah dua dari bilangan sebelumnya, dimulai dari 0
Barisan bilangan adalah suatu urutan bilangan dengan pola tertentu. Masing-masing bilangan dalam urutan tersebut disebut suku-suku barisan dan setiap suku digabungkan dengan tanda koma(,).
Contoh:
1, 5, 9, 13, 17, 21, 25, 29,….
Angka 9 merupakan suku ketiga, 17 merupakan suku kelima. 25 merupakan suku ketujuh.

1 – 10 Contoh Soal Pola Bilangan dan Jawaban
1. Tentukan 3 bilangan selanjutnya dari barisan bilangan berikut.
a. 2, 5, 8, 11, 14,….,….,….
b. 3,5,8,12,17,…,…,…
c. 2,6,18,54,162,…,…,…
d. 1,4,9,16,….,….
Jawaban :
Pembahasan :
Tiga Bilangan Selanjutnya
- a.) 2, 5, 8, 11, 14,17,20,23
- b.) 3,5,8,12,17,23,30,38
- c.) 2,6,18,54,162,468,1458,4374
- d.) 1,4,9,16,25,36,49
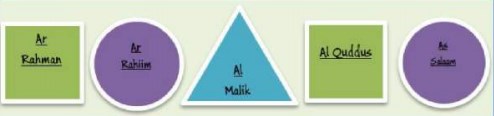
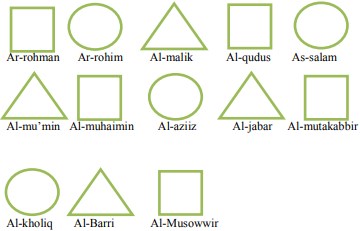
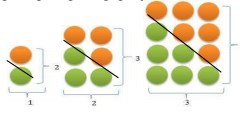
2. Selepas shalat dzuhur dan makan siang, Ali dengan teman-temannya langsung ke Pondok Pesantren El-falah untuk mengaji. Sesampainya di Pondok ternyata sedang ada pemasangan tulisan asmaul husna di dinding. Semua santri diminta oleh pak Ustad untuk membantu menempel tulisan asmaul husna dengan susunan sebagai berikut.
Berdasarkan pemaparan tersebut,selesaikan masalah-masalah berikut ini.
a. Ali dan teman-temannya membantu Pak Ustadz untuk menyusun asmaul husna sampai pola ke-13, gambar dan tuliskan nama asmaul husnanya ?
b. Tentukan jumlah masing-masing asmaul husna yang terdapat pada bentuk persegi, lingkaran dan segitiga!
Jawaban :
Pembahasan :
Menyusun dan menentukan jumlah asmaul husna :
a. Susunan ke-13 dalam asmaul husna
Jadi pola ke-13 dalam asmaul husna adalah AlMusowwir
b. Jumlah asmaul husna
3. Perhatikan barisan bilangan berikut
2,6,12,20,….,….
a. Tentukan rumus suku ke-n
b. Tentukan pola ke-7
Jawaban :
Pembahasan :
2,6,12,20,…. termasuk pola persegi panjang
Diketahui:
Bilangan 2,6,12,20,… Pola
Ditanya :
a. = Un = ?
b. pola ke-7 atau U7 = ?
Dijawab:
Misalkan
Luas Persegi Panjang ( L ) = Bilangan pada suku ( U )
Panjang = p
Lebar = tinggi = l
Pada bagian ke-n dalam Luas Persegi panjang
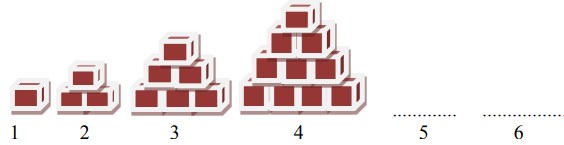
4. Perhatikan gambar berikut :
Zafir menumpuk beberapa batu bata, tumpuk pada bagian 1 berjumlah 1 buah dan tingginya 6 cm, tumpukan pada bagian 2 berjumlah 3 dan tingginya 12 cm, tumpukan pada bagian 3 berjumlah 6 dan tingginya 18 cm, begitu seterusnya.
a. Tentukan tinggi tumpukan batu bata pada bagian ke-5 dan ke-6?
b. Jika tinggi tumpukan batu bata 54 cm, tentukan banyak batu bata yang di tumpuk?
Jawaban :
Pembahasan :
Mencari tinggi dan banyaknya batu bata
a. Maka :
Bagian ke-1 =6 diperoleh dari 1 x 6
Bagian ke-2 =12 diperoleh dari 2 x 6
Bagian ke-3 =18 diperoleh dari 3 x 6
Bagian ke-4 =24 diperoleh dari 4 x 6
Bagian ke-5 =30 diperoleh dari 5 x 6
Bagian ke-6 =36 diperoleh dari 6 x 6
b. Diketahui:
Tinggi tumpukan gelas = 54 cm
Ditanya:
Banyak gelas yang ditumpuk atau Un ?
Jawab:
5. Tentukan:
a. Jumlah 10 suku pertama pada bilangan ganjil?
b. Jumlah 15 suku pertama pada bilangan genap?
Jawaban :
Pembahasan :
Mencari jumlah pada pola bilangan
- a. Jumlah 10 pada bilangan ganjil
Diketahui:
Bilangan ganjil terdiri dari 1,3,5,7,9,11,13,15,17,19,…
Ditanya: Jumlah 10 bilangan ganjil?
Jawab:
Untuk mencari jumlah bilangan ganjil, maka setiap suku pada pola bilangan ganjil tersebut di jumlahkan sampai suku ke-10
U1 + U2 + U3 + U4 + U5 + U6 + U7 + U8 + U9 + U10 = U1 + U2 + U3 + U4 + U5 + U6 + U7 + U8 + U9 + U10 = s10
1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 = 100
Jumlah S1 = 1 diperoleh dari U1
Jumlah S2 = 4 diperoleh dari U1 + U2 atau S1 + U2
Jumlah S3 = 9 diperoleh dari S2 + U3
Jumlah S4 = 16 diperoleh dari S3 + U4
Jumlah S5 = 25 diperoleh dari S4 + U5
Jumlah S6 = 36 diperoleh dari S5 + U6
Jumlah S7 = 49 diperoleh dari S6 + U7
Jumlah S8 = 64 diperoleh dari S7 + U8
Jumlah S9 = 81 diperoleh dari S8 + U9
Jumlah S10 = 100 diperoleh dari S9 + U10
karena jumlah suku pada bilangan ganjil merupakan bilangan kuadrat, maka:
Sn = n2
S10 = 102
S10 = 100
- b. Jumlah 15 pada bilangan genap
Diketahui:
Pola bilangan genap terdiri dari 2,4,6,8,10,12,…
Untuk jumlah berarti setiap suku pada pola harus dijumlahkan 2 + 4 + 6 + 8 + 10 + 12 …
Jawab:
2 + 3 + 4 + 15 + 2 + 4 + 6 + 10 … + 30
Untuk mencari Jumlah (S) pada pola bilangan genap
S1= 2 diperoleh dari U1
S2= 6 diperoleh dari U1 + U2
S3= 12 diperoleh dari S2 + U3
S4= 20 diperoleh dari S3 + U4
Seterusnya sampai S15 . dari hasil S1, S2, S3, S4 yang bilangannya 2,6,12,20 ternyata membentuk sebuah pola persegi panjang
untuk jumlah 15 pola bilangan genap dapat diperoleh dari suku ke-15 pada pola persegi panjang.
Simak Juga : Contoh Soal Penyajian Data
6. Tentukan 3 bilangan selanjutnya dari barisan bilangan berikut ini!
a. -27, -22, -17, -12,….,….,….
b. 3,5,7,9,11,…,…,…
c. 8,16,32,64,128,…,…,…
d. 1,1,2,3,5,8,13,….,….,….
Jawaban :
Pembahasan :
Tiga bilangan selanjutnya
a. -27, -22, -17, -12, -7, -2,3 setiap tingkatan selisih 5
b. 3,5,7,9,11,13,15,17 setiap tingkatan selisih 2
c. 8,16,32,64,128,256,512,1024 setiap tingkatan dikali 2
d. 1,1,2,3,5,8,13,21,34,55 termasuk bilangan fibonacci
7. Perhatikan barisan bilangan berikut ini!
1,3,6,10,12,….,….
a. Tentukan rumus suku ke-n
b. Tentukan pola ke-12
Jawaban :
Pembahasan :
1,3,6,10,15,…. termasuk pola bilangan segitiga
- a) Untuk mencari rumus suku ke-n atau Un pada pola segitiga, diperoleh dari setengah rumus suku ke-n pada pola persegi panjang
Un = n (n + 1) ( rumus suku ke-n pada persegi panjang),
yaitu Un =½ n (n + 1)
- b) Menentukan pola ke-12 adalah
Un =1/2 n (n + 1)
Un = ½ 12(12 + 1)
= 6 (13)
= 78
8. Perhatikan gambar berikut:
Anwar menumpuk beberapa gelas, tumpukan gelas pada bagian 1
berjumlah 1 buah dan tingginya 8 cm, tumpukan gelas pada bagian 2
berjumlah 4 dan tingginya 16 cm, tumpukan gelas pada bagian 3 berjumlah 9 dan tingginya 24 cm, begitu seterusnya.
a. Tentukan tinggi tumpukan gelas pada bagian ke-7 dan ke-8?
b. Jika tinggi tumpukan gelas 96 cm, tentukan banyak gelas yang di tumpuk?
Jawaban :
Pembahasan :
Menentukan tinggi tumpukan dan banyaknya tumpukan
9. Tentukan:
a. Jumlah 22 suku pertama pada bilangan genap?
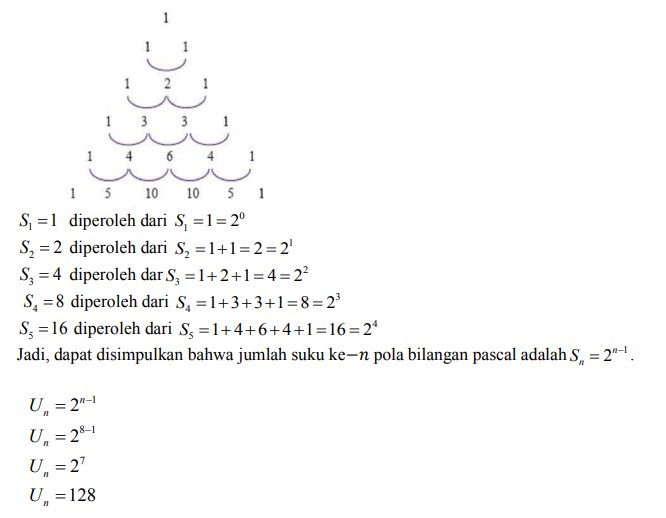
b. Jumlah bilangan pada baris ke-8 pada Segitiga Pascal?
Jawaban :
Pembahasan :
Mencari jumlah pada pola
- a. Jumlah 22 suku pertama pada pola bilangan genap
Diketahui:
Pola bilangan genap terdiri dari 2,4,6,8,10,12,…
Untuk jumlah berarti setiap suku pada pola harus dijumlahkan 2 + 4 + 6 + 8 + 10 + 12 …
Ditanya: S22 = ?
Jawab
2 + 4 + 6 + 10 + … + 44
U1 + U2 + U3 + U4 + … + U22
Untuk mencari Jumlah ( S ) pada pola bilangan genap
S1= 2 diperoleh dari U1
S2= 6 diperoleh dari U1 + U2
S3= 12 diperoleh dari S2 + U3
S4= 20 diperoleh dari S3 + U4
Seterusnya sampai S15 . dari hasil S1, S2, S3, S4 yang bilangannya 2,6,12,20 ternyata membentuk sebuah pola persegi panjang
untuk jumlah 22 pola bilangan genap dapat diperoleh dari suku ke-22 pada pola persegi panjang.
- b. Pola ke-8 pada segitiga pascal adalah
10. Diketahui suku ke-n pada suatu barisan bilangan adalah Un = 7 + 5n . Hitunglah suku ke-8 dan suku ke-24 pada barisan bilangan tersebut!
Jawaban :
Pembahasan :
Diketahui
Un = 7 + 5n
Ditanya
Suku ke-8?
Suku ke-24?
Jawab
Sudah selesai membaca dan berlatih Soal Pola Bilangan ini ? Ayo lihat dulu Soal Matematika lainnya