25+ Soal Aplikasi Turunan (Diferensial) dan Jawaban [Update]

Contoh Soal Aplikasi Turunan (Diferensial) Pilihan Ganda dan Jawaban – Secara umum sebelum mendiskusikan tema tentang turunan, perlu diingat kembali konsep tentang limit, hal ini cukup diperlukan mengingat turunan merupakan kelanjutan dari kajian tentang limit.

Teori tentang limit sebuah fungsi merupakan “akar” dari aljabar kalkulus. Oleh sebab itu uraian mengenai kalkulus selalu diawali dengan bahasan tentang limit.

Bank Soal Aplikasi Turunan (Diferensial) Pilihan Ganda dan Kunci Jawaban beserta Pembahasan untuk Siswa yang berjumlah 20 butir. Contoh Soal yang telah kami rangkum ini sering keluar dalam ulangan ataupun ujian nasional, jadi insyaallah sangat bermanfaat untuk siswa pelajari.

Turunan (diferensial) merupakan pengukuran terhadap bagaimana sebuah fungsi berubah seiring perubahan nilai yang dimasukan (input), secara umum turunan menunjukkan bagaimana suatu besaran berubah akibat perubahan besaran lainnya. Proses dalam menemukan turunan disebut diferensiasi.

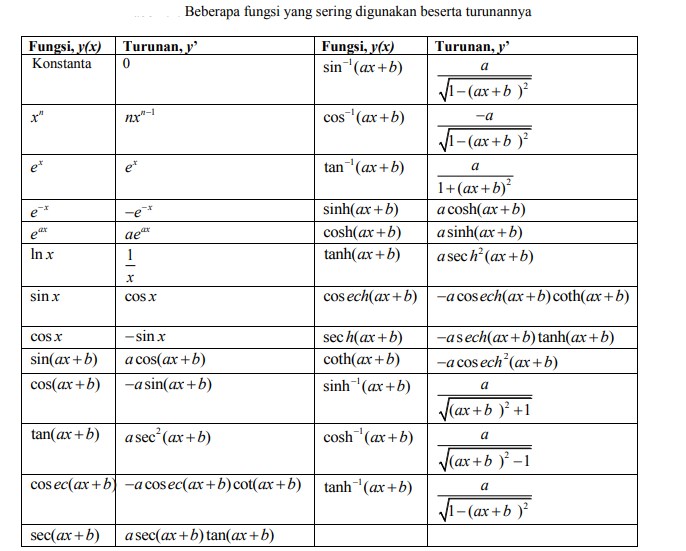
1 – 10 Soal Aplikasi Turunan (Diferensial) Beserta Jawaban dan Pembahasan

1. Tentukan persamaan garis singgung kurva y = f (x) =  5x² – 3x  di titik (2, 14) adalah. . . 

Jawaban :

2. Tentukan koordinat titik singgung dari garis singgung kurva y = f ( x ) = 3x² – 3x + 1 yang bergradien 15 adalah . . .

Jawaban :

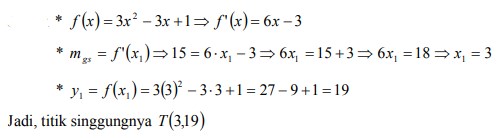
3. Tentukan persamaan garis singgung kurva f(x) = x² + 2x – 3 yang sejajar garis y = -2x + 5 adalah. . .

Jawaban : 

4. Tentukan persamaan garis singgung kurva f ( x ) = x² + 4x + 2 yang tegak lurus garis x – 2y + 6 = 0 adalah . . .

Jawaban : 

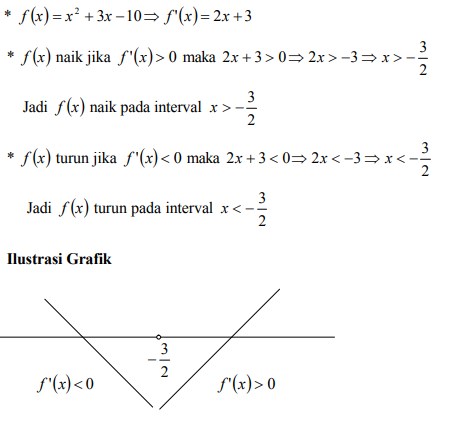
5. Tentukan interval dimana f (x) naik dan f (x) turun dari fungsi f ( x ) = x²  + 3x – 10

Jawaban : 

Baca Juga : 25+ Contoh Soal Induksi Matematika & Jawaban [+Pembahasan Lengkap]

6. Tentukan interval fungsi naik dan fungsi turun dari

Jawaban : 

7. Tentukan titik stasioner dan jenisnya dari fungsi f (x) = 2x³ – 9x² + 12x adalah . . .

Jawaban : 

8. Fungsi f (x) = ax³ + bx² memiliki titik stasioner (1, -1) tentukan nilai a dan b adalah . . .

Jawaban : 

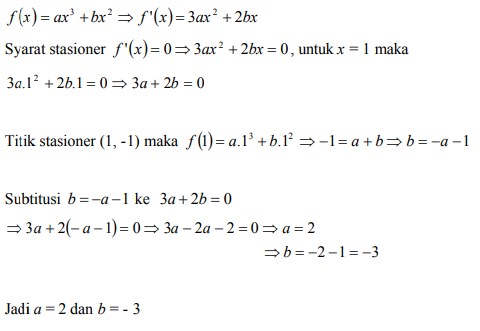
9. Tentukan nilai maksimum dan minimum dari fungsi f (x) = 2x³ + 15x² + 36x dalam interval 1 ≤ x ≤ 5

Jawaban : 

Dari nilai-nilai tersebut dapat kita lihat bahwa nilai maksimumnya adalah 55 dan nilai minimumnya adalah 23.

Penerapan Nilai Maksimum dan Minimum dalam Kehidupan Sehari-hari

10. Kebun Pak Subur berbentuk persegi panjang dengan kelilingnya 60 meter. Jika panjangnya x meter dan lebarnya y meter, tentukan:

a. Persamaan yang menyatakan hubungan antara x dan y

b. Ukuran kebun Pak Subur agar luasnya maksimum.

Jawaban : 

Dengan menguji nilai L'(x) menggunakan garis bilangan, diperoleh

11 – 20 Soal Aplikasi Turunan (Diferensial) dan Jawaban

11. Sebuah benda bergerak sepanjang garis lurus dengan panjang lintasan s meter pada waktu t detik, didefinisikan dengan persamaan s = 5 +12t – t³.

a. Tentukan rumus kecepatan saat t detik.

b. Tentukan t jika kecepatan sesaatnya nol.

c. Tentukan percepatan benda pada saat t detik.

d. Hitunglah jarak dan kecepatan sesaat jika percepatannya nol.

Jawaban : 

12. Garis g menyinggung kurva y = x³ – 3x² + 5x – 10 di titik potongnya dengan garis y=5. Persamaan garis lain yang sejajar g dan menyinggung kurva tersebut adalah ….

Jawaban : 

Titik potong kurva dengan garis y = 5

x³ – 3x² + 5x – 10 = 5

x³ – 3x² + 5x – 15 = 0

x² (x – 3) + 5(x – 3) = 0

(x² + 5)(x – 3) = 0

x² = -5 (tidak mungkin)

x = 3

m = y’ = 3x² – 6x + 5

m = 3.3² – 6.3 + 5

m = 27 – 18 + 5 = 14

cari absis titik singgung garis yang lain. Karena sejajar maka gradiennya tetap 14

m = 14

y’ = 14

3x² – 6x + 5 = 14

3x² – 6x – 9 = 0

x² – 2x – 3 = 0

(x – 3)(x + 1) = 0

x = 3 (tidak memenuhi, sebab ini adalah absis titik singgung garis g)

x = -1

y = x³ – 3x² + 5x – 10

y = (-1)³ – 3(-1)² + 5(-1) – 10

y = -1 – 3 – 5 – 10 = -19

y – y₁ = m(x – x₁)

y + 19 = 14 ( x + 1)

y + 19 = 14x + 14

y = 14x – 5

13. Diberikan suatu fungsi dengan persamaan y = 2x − √x Tentukan persamaan garis singgung kurva melalui titik (9, 16)…

Jawaban : 

Pembahasan 

Penggunaan turunan untuk menentukan persamaan garis singgung.

Turunkan fungsi untuk mendapatkan gradien dan masukkan x untuk mendapat nilainya.

14. Tentukan persamaan garis singgung pada kurva y = 2x³ – 24 di titik yang berordinat 30

Jawaban :

y = 30

2x³ – 24 = 30

2x³ = 54

x³ = 27

x = 3

m = y’ = 6x² = 6.3² = 54

y – y₁ = m(x – x₁)

y – 30 = 54 (x – 3)

y – 30 = 54x – 162

y = 54x – 132

15. Garis singgung parabola y = x² + 10x + 7 di titik yang berabsis 1 menyinggung kurva y = ax³ + b di titik yang berabsis 4. Nilai b = …

Jawaban :

Pembahasan 

x = 1 maka

y = x² + 10x + 7

y = 1² + 10.1 + 7 = 18

m = y’ = 2x + 10 = 2.1 + 10 = 12

y – y₁ = m(x – x₁)

y – 18 = 12 (x – 1)

y – 18 = 12x – 12

y = 12x + 6

y = ax³ + b

y’ = m

3ax² = 12

karena menyinggung di x = 4 maka

3a.4²=12

48a = 12

a = 1/4

Kurva menjadi y = 1/4 x³ + b

garis singgung y = 12x + 6

saat x = 4 maka y = 48 + 6 = 54

maka kurva y = 1/4 x³ + b melalui (4, 54)

54 = 1/4 . 4³ + b

54 = 16 + b

b = 38

Baca Juga : Soal Persamaan Kuadrat Pilihan Ganda dan Jawaban [+Pembahasan]

16. Sebuah benda bergerak dengan persamaan gerak y = 5t² − 4t + 8 dengan y dalam meter dan t dalam satuan detik. Tentukan kecepatan benda saat t = 2 detik . . .

Jawaban : 

Pembahasan 

Persamaan kecepatan benda diperoleh dengan menurunkan persamaan posisi benda.

y = 5t² − 4t + 8

ν = y ‘ = 10t − 4

Untuk t = 2 detik dengan demikian kecepatan benda adalah

ν = 10(2) − 4 = 20 − 4 = 16 m/detik

17. Persamaan garis yang menyinggung kurva y = x³ + 2x² − 5x di titik (1, −2) adalah….

Jawaban : 

Pembahasan 

Tentukan dulu gradien garis singgung

y = x³ + 2x² − 5x

m = y ‘ = 3x² + 4x − 5

Nilai m diperoleh dengan memasukkan x = 1

m = 3(1)² + 4(1) − 5 = 2

Persamaan garis dengan gradiennya 2 dan melalui titik (1, −2) adalah

y − y₁ = m(x − x₁)

y − (−2) = 2(x − 1)

y + 2 = 2x − 2

y = 2x – 4

18. Tentukan nilai maksimum dari fungsi f(x) = 3x(x² − 12) adalah. . .

Jawaban : 

Pembahasan 

Nilai maksimum diperoleh saat f ‘(x) = 0

Urai kemudian turunkan

f(x) = 3x(x² − 12)

f(x) = 3x³ − 36x

f ‘(x) = 9x² − 36 = 0

9x² = 36

x² = 4

x = √4 = ±2

Untuk x = +2

f(x) = 3x³ − 36x = 3(2)³ − 36(2) = 24 − 72 = − 48

Untuk x = −2

f(x) = 3x³ − 36x = 3(−2)³ − 36(−2) = −24 + 72 = 48

Dengan demikian nilai maksimumnya adalah 48

19. Tentukan persamaan garis singgung pada kurva y = 2x³ – 24 di titik yang berordinat 30 adalah . . .

Jawaban : 

Pembahasan 

y = 30

2x³ – 24 = 30

2x³ = 54

x³ = 27

x = 3

m = y’ = 6x² = 6.3² = 54

y – y₁ = m(x – x₁)

y – 30 = 54 (x – 3)

y – 30 = 54x – 162

y = 54x – 132

20. Tentukan persamaan garis singgung pada kurva y = x⁴ – 3x³ + 6x + 7 di titik yang berabsis 2 adalah. . .

Jawaban : 

Pembahasan 

x = 2

y = x⁴ – 3x³ + 6x + 7

y = 2⁴ – 3.2³ + 6.2 + 7 = 16 – 24 + 12 + 7 = 11

m = y’ = 4x³ – 9x² + 6 = 4.2³ – 9.2² + 6 = 32 – 36 + 6 = 2

y – y₁ = m(x – x₁)

y – 11 = 2 (x – 2)

y – 11 = 2x – 4

y = 2x + 7

21. Tentukan persamaan garis singgung pada kurva y = x² + 8x + 1 yang tegak lurus pada garis x + 2y – 4 = 0.

Jawaban : 

Diketahui :

kurva y = x² + 8x + 1

Garis x + 2y – 4 = 0

Ditanyakan : persamaan garis singgung pada kurva yang tegak lurus dengan garis x + 2y – 4 = 0

Jawab:

Gradien garis singgung kurva y = x² + 8x + 1 adalah y’ = m₁ = 2x + 8.

Garis x + 2y – 4 = 0 atau y = –¹/₂ x + 4 mempunyai gradien m₂ = –¹/₂

Karena garis singgung pada kurva y = x² + 8x + 1 tegak lurus dengan garis y = –¹/₂ x + 4 maka haruslah m₁.m₂ = -1

m₁ (-¹/₂) = -1

m₁ = 2

Untuk m₁ = 2 maka diperoleh 2 = 2x + 8, sehingga x = -3

Untuk x = -3 diperoleh y = (-3)² + 8. (-3) + 1 = 14, sehingga koordinat titik singgungnya adalah (-3,-14).

Persamaan garis singgungnya adalah

y + 14 = 2 (x + 3)

y + 14 = 2x + 6

y = 2x – 8

Jadi, persamaan garis singgungnya adalah y = 2x – 8

22. Jarak yang ditempuh sebuah mobil dalam waktu t diberikan oleh fungsi f (t) = ¹/₃t³ – 4t² + 20t + 2 km

a. Tentukan persamaan kecepatan dan percepatan dari fungsi tersebut.

b. Tentukan pada waktu (jam) ke berapa mobil itu mencapai kecepatan tertinggi? Tentukan pula kecepatan tertinggi mobil tersebut.

Jawaban : 

Diketahui : fungsi jarak s (t) = ¹/₃t³ – 4t² + 20t + 2 km

Ditanyakan :

a. Tentukan persamaan kecepatan dan percepatan dari fungsi tersebut.

b. Tentukan pada waktu (jam) ke berapa mobil itu mencapai kecepatan tertinggi? Tentukan pula kecepatan tertinggi mobil tersebut.

Jawab:

23. Ditentukan fungsi f (x) = x³ – 27x + 10 tentukan :

a. Turunan pertama dan kedua fungsi tersebut.

b. Tentukan nilai stasioner dan titik stasioner.

c. Tentukan titik balik maksimum, titik balik minimum, nilai balik maksimum, nilai balik minimum, titik belok (disertakan dengan uji turunan pertama)

Jawaban : 

Diketahui : f (x) = x³ – 27x + 10

Ditanyakan :

a. Turunan pertama dan kedua fungsi tersebut.

b. Tentukan nilai stasioner dan titik stasioner.

c. Tentukan titik balik maksimum, titik balik minimum, nilai balik maksimum, nilai balik minimum, titik belok (disertakan dengan uji turunan pertama)

Jawab :

a. Turunan pertama fungsi adalah f'(x) = 3x² – 27

Turunan kedua fungsi adalah f”(x) = 6x

b. Nilai stasioner f'(x) = 0

3x² – 27 = 0

x² – 9 = 0

(x – 3) (x + 3) = 0

x =3 V x = -3

Untuk x = 3 , diperoleh y = 3³ – 27.3 + 10 = -44

Untuk x = -3 , diperoleh y = (-3)³ – 27 (-3) + 10 = 64

Jadi, fungsi f (x) = x³ – 27x + 10 mempunyai nilai stasioner f (3) = -44 dan f(-3) = 64, serta titik stasionernya adalah (3, -44) dan (-3, dan 64).

c. Turunan pertama fungsi adalah f'(x) = 3x² – 27

Uji turunan pertama

Dari uji turunan pertama diatas, diperoleh Titik balik maksimum adalah (-3, 64) , Titik balik minimum adalah (3, -44), Nilai balik maksimum adalah f(-3) = 64, Nilai balik minimum adalah f(3) = -44

Titik belok

f”(x) = 0

6x = 0 ⇒ x = 0

Untuk x = 0, diperoleh y = 10

Jadi, titik belok fungsi f(x) = x³ – 27x + 10 adalah (0, 10)

24. Suatu perusahaan tekstil menghasilkan x celana jeans dengan biaya total sebesar 20x – 75 + x² ribu rupiah. Jika semua celana jeans terjual dengan harga Rp 100.000,- untuk setiap celana jeans, berapa keuntungan maksimum yang diperoleh perusahaan tersebut!

Jawaban : 

Diketahui :

perusahaan memproduksi = x celana jeans

Biaya total : 20x – 75 + x² ribu rupiah

Harga 1 celana jeans = Rp 100.000,-

Ditanyakan : Berapa keuntungan maksimum yang diperoleh perusahaan?

Jawab :

25. Selembar karton berbentuk persegi panjang dengan ukuran panjang 16 cm dan lebar 10 cm. kertas karton itu akan dibuat menjadi kotak tanpa tutup dengan cara memotong empat bagian pojoknya sehingga diperoleh kotak tanpa tutup seperti diperlihatkan pada gambar :

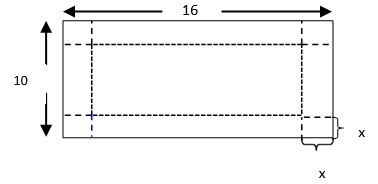
a. Jika volume kotak tanpa tutup itu dilambangkan dengan V, nyatakan V sebagai fungsi dari x.

b. Tentukan nilai x agar V mencapai maksimum

c. Hitunglah nilai V yang maksimum itu.

Jawaban : 

Sudah selesai membaca dan berlatih soal ini ? Ayo lihat dulu Soal Matematika lainnya

Posting terkait:

29+ Contoh Soal Garis dan Sudut dan Jawaban [Update]

Contoh Soal Penyajian Data dan Jawaban [Update]

25+ Soal Operasi Hitung Bentuk Aljabar dan Jawaban [Update]