Contoh Soal Induksi Matematika dan Jawaban – Induksi matematika merupakan metode pembuktian yang sering digunakan untuk menentukan kebenaran dari suatu pernyataan yang diberikan dalam bentuk bilangan asli.
Induksi matematika adalah teknik pembuktian yang baku didalam matematika. Induksi matematika dapat melakukan pembuktian kebenaran suatu pernyataan matematika yang berhubungan dengan bilangan asli, bukan untuk menemukan formula.

Prinsip Induksi Matematika
Langkah Awal (basic Step): P(1) benar.
Langkah Induksi (induction Step): jika P(k) benar,
maka P(k+1)benar, untuk setiap k bilangan asli.
Pada proses pembuktian dengan prinsip Induksi Matematika, untuk langkah awal tidak selalu dipilih untuk n=1, n= 2, dan n= 3, tetapi dapat dipilih sembarang nilai n sedemikian hingga dapat mempermudah supaya langkah awal terpenuhi.
1 – 10 Soal Induksi Matematika dan Jawaban
1. Buktikan bahwa pernyataan dibawah bernilai benar untuk n bilangan asli dan tentukan jumlah tujuh suku pertamannya !
Jawaban :
Pembuktian :
Jumlah tujuh suku pertama :
2. Buktikan bahwa pernyataan dibawah bernilai benar untuk n bilangan asli dan tentukanlah suku kesepuluhnya !
Jawaban :
Pembuktian :
suku kesepuluh :
3. Gunakan induksi matematik untuk membuktikan bahwa jumlah n buah bilangan ganjil positif pertama adalah n² adalah . . .
Jawaban :
(i) Basis induksi: Untuk n = 1, jumlah satu buah bilangan ganjil positif pertama adalah 12 = 1. Ini benar karena jumlah satu buah bilangan ganjil positif pertama adalah 1.
(ii) Langkah induksi: Andaikan p(n) benar, yaitu pernyataan :
Karena langkah basis dan langkah induksi keduanya telah diperlihatkan benar, maka jumlah n buah bilangan ganjil positif pertama adalah n².
4. Untuk semua bilangan bulat tidak-negatif n, buktikan dengan induksi matematik bahwa 20 + 21 + 22 + … + 2n = 2n+1 – 1
Jawaban :
(i) Basis induksi.
Untuk n = 0 (bilangan bulat tidak negatif pertama), kita peroleh: 20 = 20+1 – 1.
Ini jelas benar, sebab 20 = 1 = 20+1 – 1
= 21 – 1
= 2 – 1
= 1
(ii) Langkah induksi. Andaikan bahwa p(n) benar, yaitu
20 + 21 + 22 + … + 2n = 2n+1 – 1
adalah benar (hipotesis induksi). Kita harus menunjukkan bahwa p(n +1) juga benar, yaitu
20 + 21 + 22 + … + 2n + 2n+1 = 2(n+1) + 1 – 1
juga benar. Ini kita tunjukkan sebagai berikut:
20 + 21 + 22 + … + 2n + 2n+1 = (20 + 21 + 22 + … + 2n) + 2n+1
= (2n+1 – 1) + 2n+1 (hipotesis induksi)
= (2n+1 + 2n+1) – 1
= (2 . 2n+1) – 1
= 2n+2 – 1
= 2(n+1) + 1 – 1
Karena langkah 1 dan 2 keduanya telah diperlihatkan benar, maka untuk semua bilangan bulat tidak-negatif n, terbukti bahwa 20 + 21 + 22 + … +132n = 2n+1 – 1¾
5. Untuk tiap n ≥ 3 jumlah sudut dalam sebuah poligon dengan n sisi adalah 180(n − 2)°. Buktikan pernyataan ini dengan induksi matematik.
Jawaban :
Basis, Untuk nilai n = 3, poligon akan berbentuk segitiga dengan jumlah sudut 180°. Jumlah sisi sebanyak 3 sehingga 180(3 − 2) = 180°. Jadi untuk n = 3 proposisi benar
Induksi, Asumsikan bahwa jumlah sudut dalam poligon dengan n sisi yaitu 180(n − 2)° adalah benar (hipotesis induksi).
Kita ingin menunjukkan bahwa jumlah sudut poligon yang memiliki n+1 sisi yaitu 180(n − 1)°
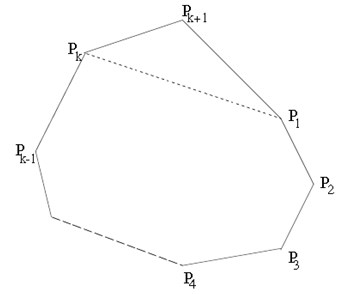
Pada gambar diatas dapat ditunjukkan terdapat dua bagian yaitu segitiga P1PnPn+1 dan poligon dengan n sisi Jumlah sudut dalam poligon n sisi menurut asumsi yaitu 180(n − 2)° dan jumlah sudut di dalam untuk segitiga yaitu 180◦.
Jadi jumlah sudut dalam dari poligon dengan n + 1 sisi yaitu 180(n − 2)° + 180° = 180(n − 1)°.
Karena basis dan langkah induksi benar, maka proposisi di atas terbukti benar.
Baca Juga : Soal Pertidaksamaan Nilai Mutlak
6. Buktikan pernyataan “Untuk membayar biaya pos sebesar n sen (n ≥ 8) selalu dapat digunakan hanya perangko 3 sen dan perangko 5 sen” benar
Jawaban :
(i) Basis induksi. Untuk membayar biaya pos 8 sen dapat digunakan 1 buah perangko 3 sen dan 1 buah perangka 5 sen saja. Ini jelas benar.
(ii) Langkah induksi. Andaikan p(n) benar, yaitu untuk membayar biaya pos sebesar n (n ≥ 8) sen dapat digunakan perangko 3 sen dan 5 sen (hipotesis induksi). Kita harus menunjukkan bahwa p(n +1) juga benar, yaitu untuk membayar biaya pos sebesar n + 1 sen juga dapat menggunakan perangko 3 sen dan perangko 5 sen. Ada dua kemungkinan yang perlu diperiksa:
Kemungkinan pertama, misalkan kita membayar biaya pos
senilai n sen dengan sedikitnya satu perangko 5 sen. Dengan mengganti satu buah perangko 5 sen dengan dua buah perangko 3 sen, akan diperoleh susunan perangko senilai n + 1 sen.
Kemungkinan kedua, jika tidak ada perangko 5 sen yang digunakan, biaya pos senilai n sen menggunakan perangko 3
sen semuanya. Karena n ≥ 8, setidaknya harus digunakan tiga buah perangko 3 sen. Dengan mengganti tiga buah perangko 3 sen dengan 2 buah perangko 5 sen, akan dihasilkan nil1a8i perangko n + 1 sen ¾
7. Bilangan bulat positif disebut prima jika dan hanya jika bilangan bulat tersebut habis dibagi dengan 1 dan dirinya sendiri. Kita ingin membuktikan bahwa setiap bilangan bulat positif n (n ≥ 2) dapat dinyatakan sebagai perkalian dari (satu atau lebih) bilangan prima. Buktikan dengan prinsip induksi kuat.
Jawaban :
Basis induksi. Jika n = 2, maka 2 sendiri adalah bilangan prima dan di sini 2 dapat dinyatakan sebagai perkalian dari satu buah bilangan prima, yaitu dirinya sendiri.
Langkah induksi. Misalkan pernyataan bahwa bilangan 2, 3, …, n dapat dinyatakan sebagai perkalian (satu atau lebih) bilangan prima adalah benar (hipotesis induksi). Kita perlu menunjukkan bahwa n + 1 juga dapat dinyatakan sebagai perkalian bilangan prima. Ada dua kemungkinan nilai n + 1:
a) Jika n + 1 sendiri bilangan prima, maka jelas ia dapat dinyatakan sebagai perkalian satu atau lebih bilangan prima.
Jika n + 1 bukan bilangan prima, maka terdapat bilangan bulat positif a yang membagi habis n + 1 tanpa sisa. Dengan kata lain,
(n + 1)/ a = b atau (n + 1) = ab
yang dalam hal ini, 2 ≤ a ≤ b ≤ n. Menurut hipotesis induksi, a dan b dapat dinyatakan sebagai perkalian satu atau lebih bilangan prima. Ini berarti, n + 1 jelas dapat dinyatakan sebagai perkalian bilangan prima, karena n + 1 = ab.
Karena langkah (i) dan (ii) sudah ditunjukkan benar, maka terbukti bahwa setiap bilangan bulat positif n (n ≥ 2) dapat dinyatakan sebagai perkalian dari (satu atau lebih) bilangan prima.
9. Buktikan 1 + 2 + 3 + … + n = n/2 (n + 1) dengan menggunakan induksi matematika!
Jawaban :
10. Buktikan bahwa 1 + 2 + 3 + … + n = ½ n(n+1) untuk setiap n bilangan integer positif adalah. . .
Jawaban :
Basis : Untuk n = 1 akan diperoleh :
1 = ½ 1 . (1+1) → 1 = 1
Induksi : misalkan untuk n = k asumsikan 1 + 2 + 3 + …+ k = ½ k (k+1)
Untuk n = k+1 berlaku
1 + 2 + 3 + …+ (k+1) = ½ (k+1) (k+2)
Penyelesaian :
11 – 15 Contoh Soal Induksi Matematika dan Jawaban
11. Buktikan bahwa 1 + 3 + 5 + … + n = (2n – 1) = n2 untuk setiap n bilangan bulat positif adalah. . .
Jawaban :
Basis : Untuk n = 1 akan diperoleh :
1 = 12 → 1 = 1
Induksi : misalkan untuk n = k asumsikan 1 + 3 + 5 + …+ (2k – 1) = k2
Untuk n = k + 1 berlaku
12. Buktikan bahwa N3 + 2n adalah kelipatan 3 untuk setiap n bilangan bulat positif adalah. . .
Jawaban :
Basis : Untuk n = 1 akan diperoleh :
1 = 13 + 2(1) → 1 = 3 , kelipatan 3
Induksi : misalkan untuk n = k asumsikan k 3 + 2k = 3x
adib. Untuk n = k + 1 berlaku
(k + 1)3 + 2(k + 1) adalah kelipatan 3
(k 3 + 3k 2 + 3 k+1) + 2k + 2
(k 3 + 2k) + (3k 2 + 3k + 3)
(k 3 + 2k) + 3 (k 2 + k + 1)
Induksi
3x + 3 (k 2 + k + 1)
3 (x + k 2 + k + 1)
Kesimpulan : N 3 + 2n adalah kelipatan 3
Untuk setiap bilangan bulat positif n
13. Buktikan bahwa 2n > n + 20, untuk setiap bilangan bulat n ≥ 5 adalah. . .
Jawaban :
14. Buktikan bahwa 22n-1 habis dibagi 3 untuk semua bilangan bulat n ≥ 1 adalah. . .
Jawaban :
15. Buktikan bahwa setiap bilangan bulat positif n yang lebih besar atau sama dengan 2 merupakan bilangan prima atau hasil kali beberapa bilangan prima.
Jawaban Soal Induksi Matematika :
Pembahasan :
Misalkan P(n) adalah proposisi bahwa setiap bilangan bulat positif n yang lebih besar atau sama dengan 2 merupakan bilangan prima atau hasilkali beberapa bilangan prima.
Basis induksi.
Untuk n = 2, karena 2 adalah bilangan prima, maka pernyataan tersebut benar.
Langkah induksi
Misalkan P(k) benar, yaitu asumsikan bahwa 2,3,…,k dapat dinyatakan sebagai perkalian (satu atau lebih) bilangan prima (hipotesis induksi), akan ditunjukkan bahwa P(k+1) juga benar, yaitu n+1 juga dapat dinyatakan sebagai perkalian bilangan prima.
Ada 2 kasus:
Jika k+1 sendiri bilangan prima, maka jelas ia dapat dinyatakan sebagai perkalian satu atau lebih bilangan prima.
Jika k+1 bukan bilangan prima, maka terdapat bilangan bulat positif a yang habis membagi k+1 tanpa sisa. Dengan kata lain ,
(k + 1)/a = b ,atau (k + 1) = ab
Yang dalam hal ini, 2 ≤ a ≤ b ≤ k. Menurut hipotesis induksi, a dan b dapat dinyatakan sebagai perkalian satu atau lebih bilangan prima. Ini berarti, k+1 jelas dapat dinyatakan sebagai perkalian bilangan prima, karena k+1 = ab.
Karena (1) dan (2) benar, maka terbukti bahwa setiap bilangan bulat positif n (n ≥ 2) dapat dinyatakan sebagai perkalian satu atau lebih bilangan prima.
Sudah selesai membaca dan berlatih Soal Induksi Matematika ini ? Ayo lihat dulu Soal Matematika lainnya














Buktikan bahwa penjumlahan n bilangan asli berurutan berlaku: 1 + 2 + 3 + 4 + 5 + … + n= n(n+1) / 2 HOTS