Contoh Soal Pertidaksamaan Nilai Mutlak dan Jawaban – Pertidaksamaan nilai mutlak merupakan pertidaksamaan yang selalu benar untuk setiap nilai pengganti variabel. Suatu pertidaksamaan nilai mutlak selalu salah untuk setiap pengganti variabelnya disebut pertidaksamaan palsu (fake). Definisi Pertidaksamaan yang Memuat Nilai Mutlak Pertidaksamaan nilai mutlak adalah pertidaksamaan yang variabelnya di dalam tanda mutlak. Pertidaksamaan nilai mutlak dapat diselesaikan dengan menggunakan konsep dasar dari sifat persamaan nilai mutlak.

Persamaan |x| = 5 meminta kita untuk menentukan semua bilangan x yang memiliki jarak 5 dengan titik 0, sedangkan pertidaksamaan |x| < 5 meminta kita untuk menentukan semua bilangan x yang memiliki jarak kurang dari 5 dengan titik 0.
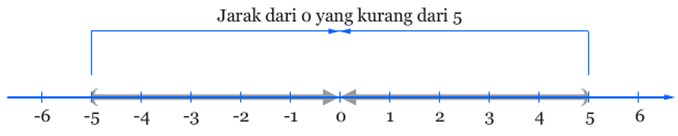
Seperti ilustrasi dari gambar di atas, selesaian dari pertidaksamaan |x| < 5 adalah x > –5 dan x < 5, yang juga dapat dituliskan ke dalam pertidaksamaan gabungan –5 < x < 5. Ilustrasi ini dapat digunakan untuk membangun konsep sifat pertidaksamaan nilai mutlak berikut.
Sifat I: Pertidaksamaan Nilai Mutlak
Jika X adalah suatu bentuk aljabar dan k adalah bilangan real positif, maka |X| < k akan mengimplikasikan –k < X < k.
Contoh sederhana :
Pertidaksamaan Nilai Mutlak “Kurang Dari”
Tentukan himpunan selesaian dari pertidaksamaan-pertidaksamaan: |3x + 2|/4 ≤ 1 dan |2x – 7| < –5.
Pembahasan
Untuk menyelesaikan pertidaksamaan |3x + 2|/4 ≤ 1, kita harus mengisolasi simbol nilai mutlak di satu ruas.
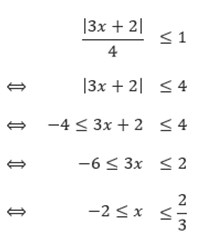
Sehingga, himpunan selesaian dari pertidaksamaan |3x + 2|/4 ≤ 1 adalah {x | –2 ≤ x ≤ 2/3, x bilangan real}.
Selanjutnya, perhatikan pertidaksamaan |2x – 7| < –5.
Karena nilai mutlak dari setiap bilangan adalah positif atau nol, maka himpunan selesaian dari pertidaksamaan tersebut adalah himpunan kosong
1 – 10 Soal Pertidaksamaan Nilai Mutlak dan Pembahasan
1. Carilah himpunan penyelesaian dari pertidaksamaan | x + 1 | < 3 adalah . . .
Jawaban :
2. Selesaikanlah dari pertidaksamaan | x + 3 | < 2 – x adalah . . .
Jawaban :
3. Selesaikanlah | 3x + 7|> | 4x -8 | adalah. . .
Jawaban :
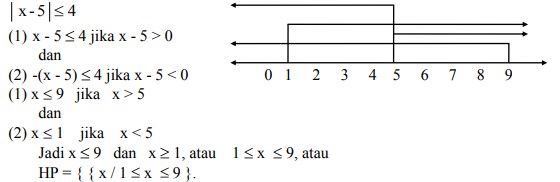
4. Carilah himpunan penyelesaian dari pertidaksamaan harga mutlak | x – 5 | ≤ 4 adalah . . .
Jawaban :
Menurut definisi harga mutlak
5. Carilah himpunan penyelesaian | x² – 10 | < 6
Jawaban :
Cara Pertama :
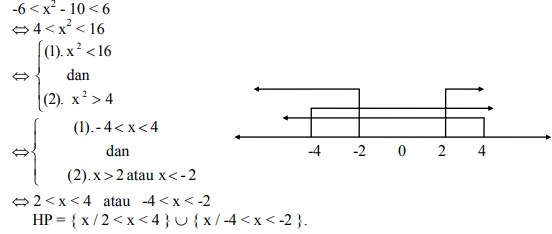
Cara kedua :
Simak Juga : Soal Persamaan Nilai Mutlak
6. Buktikanlah, bahwa untuk setiap x, y, z ∈ R berlaku | x – y| ≤ | x – z | + | z – y | adalah. . .
Jawaban :
7. Selesaikanlah pertidaksamaan | 3x + 2| > 5 adalah. . .
Jawaban :
8. Selesaikanlah pertidaksamaan | 3x + 2| > | 3x + 2| adalah. . .
Jawaban :
| 3x + 2| > | 3x + 2|
9. Tentukan penyelesaianya dan lukiskan garis bilangannya dari 10 – 5x < 2x – 11 adalah. . .
Jawaban :
10. Selesaikan pertidaksamaan berikut :
| 2x – 1 |≤ 9
Jawaban :
Berdasarkan definisi nilai mutlak, diperoleh
| 2x – 1 |≤ 9
11 – 20 Soal Pertidaksamaan Nilai Mutlak dan Jawaban
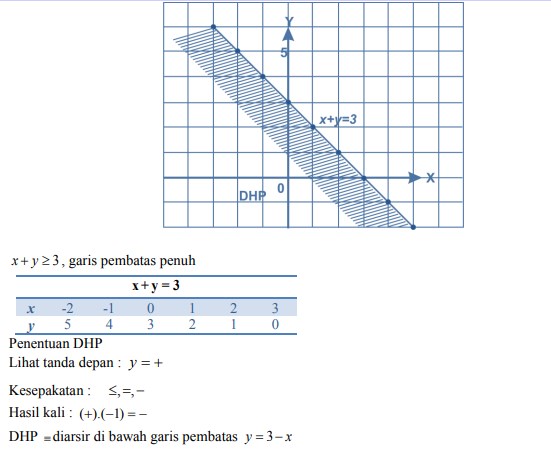
11. Lukiskan daerah himpunan penyelesaian (DHP) dari pertidaksamaan x + y ≥ 3 adalah. . .
Jawaban :
12. Tentukanlah himpunan penyelesaian dari |x – 2014| ≤ 6
Jawaban :
13. Tentukan penyelesaian dari pertidaksamaan harga mutlak dari | 2x – 3 | ≥ 5 adalah. . .
Jawaban :
14. Tentukan himpunan penyelesaian dari pertidaksamaan nilai mutlak |x + 7 |< 9 adalah . . .
Jawaban :
Cara menyelesaikan pertidaksamaan mutlak ini sebagai berikut.
-9 < x+7 < 9
-9 – 7 < x < 9 – 7
-16 < x < 2
Jadi, himpunan penyelesaiannya adalah { x/ -16 < x < 2}
15. Tentukan himpunan penyelesaian dari pertidaksamaan nilai mutlak |2x – 1 | ≥ 7 adalah . . .
Jawaban :
Cara menyelesaikan pertidaksamaan mutlak ini dibagi menjadi dua bagian
(Bagian 1)
2x – 1 ≥ 7
2x ≥ 7 + 1
2x ≥ 8
x ≥ 4
(Bagian 2)
2x – 1 ≤ -7
2x ≤ -7 + 1
2x ≤ -6
x ≤ -3
Jadi, himpunan penyelesaiannya adalah { x/ x ≤ -3 atau x ≥ 4}
Baca Juga : Soal Matriks, Determinan dan Invers
16. Tentukan himpunan penyelesaian dari pertidaksamaan nilai mutlak | x + 3 | ≤ | 2x – 3 | adalah . . .
Jawaban :
Kalau dalam bentuk soal ini, langkah menyelesaikan pertidaksamaannya dengan mengkuadratkan kedua ruas.
Perhatikan proses berikut ini :
(x + 3)2 ≤ (2x – 3)2
(x + 3)2 – (2x – 3)2 ≤ 0
(x + 3 + 2x – 3) – (x + 3 – 2x + 3) ≤ 0 (ingat: a2 – b2 = (a+b)(a-b))
x (6 – x) ≤ 0
Pembuat nol adalah x = 0 dan x = 6
Mari selidiki menggunakan garis bilangan
Oleh karena batasnya ≤ 0, maka penyelesaiannya adalah x ≤ 0 atau x ≥ 6. Jadi, himpunan penyelesaiannya adalah {x/ x ≤ 0 atau x ≥ 6}.
Mari selidiki menggunakan garis bilangan
Oleh karena batasnya ≤ 0, maka penyelesaiannya adalah x ≤ 0 atau x ≥ 6.
Jadi, himpunan penyelesaiannya adalah {x/ x ≤ 0 atau x ≥ 6}.
17. Tentukan himpunan penyelesaian dari pertidaksamaan nilai mutlak | 3x + 1 | – | 2x + 4 | > 10 adalah . . .
Jawaban :
Menyelesaikan pertidaksamaan nilai mutlak seperti ini lebih mudah menggunakan cara menjabarkan definisi.
Prinsipnya adalah batasan-batasan pada fungsi nilai mutlaknya.
Perhatikan pada 3x + 1 dan 2x + 4
Dari batasan batasan itu maka dapat diperoleh batasan-batasan nilai penyelesaian seperti pada garis bilangan di bawah ini.
Dengan garis bilangan tersebut maka pengerjaanya dibagi menjadi 3 bagian daerah penyelesaian.
(1) Untuk batasan x ≥ -1/3 ……(1)
(3x + 1) – (2x + 4) < 10
3x + 1 – 2x- 4 < 10
x- 3 < 10
x < 13 …….(2)
Dari (1) dan (2) diperoleh irisan penyelesaian -1/3 ≤ x < 13
(2) Untuk batasan -2 ≤ x < -1/3 ……(1)
-(3x + 1) – (2x + 4) < 10
-3x – 1 – 2x – 4 < 10
-5x – 5 < 10
-5x < 15
-x < 3
x > 3 …….(2)
Dari (1) dan (2) tidak diperoleh irisan penyelesaian atau tidak ada penyelesaian.
(3) Untuk batasan x < -2 ……(1)
-(3x + 1) + (2x + 4) < 10
-3x – 1 + 2x + 4 < 10
-x + 3 < 10
-x < 7
x > -7 …….(2)
Dari (1) dan (2) diperoleh irisan penyelesaian -7 < x < -2.
Jadi, himpunan penyelesaiannya adalah {x/ -1/3 ≤ x < 13 atau -7 < x < -2}.
18. Tentukan himpunan penyelesaian dari pertidaksamaan nilai mutlak | 3 – 2x | < 4 adalah . . .
Jawaban :
19. Tentukan himpunan penyelesaian dari pertidaksamaan nilai mutlak | ½x + 6 | ≥ 9 adalah . . .
Jawaban :
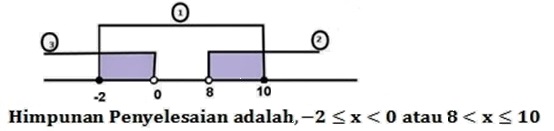
20. Tentukan himpunan penyelesaian dari pertidaksamaan nilai mutlak 2 < | 2 – ½x | ≤ 3 adalah . . .
Jawaban :
↔ | 2 – ½x | ≤ 3
-3 ≤ 2 – ½x ≤ 3
-5 ≤ – ½x ≤ 1
10 ≥ x ≥ -2 atau -2 ≤ x ≤ 10 …(1)
↔ | 2 – ½x | > 2
Untuk 2 – ½x < -2 atau 2 – ½x > 2
2 – ½x < 2
x > 8 …(2)
2 – ½x > 2
x < 0 …(3)
Dari (1), (2) dan (3) :
21 – 35 Soal Pertidaksamaan Nilai Mutlak dan Penyelesaian
21. Tentukan himpunan penyelesaian pertidaksamaan |𝑥 + 2| ≤ |𝑥 − 3|!
Jawaban :
22. Tentukan himpunan penyelesaian pertidaksamaan |𝑥 + 3| ≤ |𝑥 − 1|!
Jawaban :
23. Himpunan penyelesaian dari |2𝑥 − 1| ≤ 5 adalah…
Jawaban :
24. Himpunan penyelesaian dari |𝑥 + 2| ≤ 3 adalah…
Jawaban :
25. Pada suatu hari rata-rata kepadatan lalu lintas di suatu perempatan adalah 726 mobil per jam (mpj). Selama jam sibuk kepadatan lalu lintasnya lebih tinggi, sedangkan selama jam longgar kepadatannya lebih rendah. Tentukan jangkauan dari kepadatan lalu lintas di perempatan tersebut jika kepadatannya tidak pernah lebih atau 235 mpj dari rata-rata!
Jawaban :
Pembahasan :
Kepadatan lalu lintas diperempatan tersebut tidak pernah lebih atau kurang 235 mpj dari rata -rata. Misalkan v adalah kepadatan lalu lintas diperempatan tersebut, maka selisih v dan 726 harus kurang dari atau sama dengan 235, atau dapat dimodelkan menjadi :
26. Tentukan selesaian pertidaksamaan berikut dengan benar dan rinci!
Pada mobil-mobil baru, angka kilometer per liternya tergantung pada bagaimana mobil itu gunakan, apakah sering digunakan untuk perjalanan jauh ataukah hanya untuk perjalanan jarak dekat (dalam kota). Untuk suatu merk mobil tertentu, angka kilometer perliternya berkisar 2,8 kurang atau lebihnya dari 12 km/l. Berapakah jangkauan dari angka Km/l dari mobil tersebut.
Jawaban :
Pembahasan :
Misalkan m angka km/L dari mobil tersebut.
Maka selisih m dan 12 tidak boleh kurang dari 2,8 atau dapat dimodelkan sebagai berikut:
27. Tentukan batas-batas nilai x yang memenuhi pertidaksamaan |𝑥 + 2| ≤ |𝑥 − 3|!
Jawaban :
28. Tentukan himpunan pertidaksamaan |𝑥 + 2| ≤ 3!
Jawaban :
29. Tentukan selesaian pertidaksamaan berikut dengan rinci! Pada mobil-mobil baru, angka kilometer per liternya tergantung pada bagaimana mobil itu digunakan, apakah sering digunakan untuk perjalanan jauh ataukah hanya untuk perjalanan jarak dekat (dalam kota). Untuk suatu merk mobil tertentu, angka kilometer perliternya berkisar 2,8 kurang atau lebihnya dari 12 km/L. Berapakah jangkauan dari angka km/L dari mobil tersebut.
Jawaban :
Pembahasan :
Misalkan m angka km/L dari mobil tersebut. Maka selisih m dan 12 tidak boleh kurang dari 2,8 atau dapat dimodelkan sebagai berikut:
30. Tentukan himpunan penyelesaian dari pertidaksamaan nilai mutlak berikut:
a) | x+4 |≤6
b) | 3x-1|>8
Jawaban :
Pembahasan :
31. Tentukan interval nilai x yang memenuhi | 2x + 6 | > 4 adalah. . .
Jawaban :
Pembahasan :
32. Tentukan interval nilai x yang memenuhi pertidaksamaan |2x + 3 | < 5 adalah. . .
Jawaban :
Pembahasan :
33. Tentukan interval nilai x yang memenuhi pertidaksamaan |2x – 9 | < 4x – 3 adalah. . .
Jawaban :
Pembahasan :
34. Tentukan interval nilai x yang memenuhi pertidaksamaan |x + 4 | ≥ | 3x – 8 | adalah. . .
Jawaban :
Pembahasan :
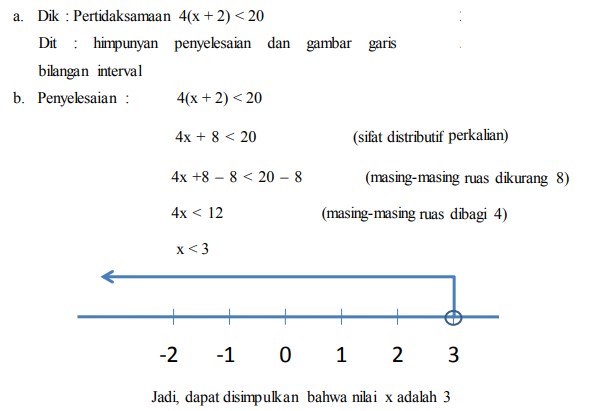
35. Terdapat pertidaksamaan 4(x + 2) < 20 !
a) Carilah himpunan penyelesaian dari pertidaksamaan diatas.
b) Gambarkanlah garis bilangan untuk melihat interval.
Jawaban :
Pembahasan :
Sudah selesai membaca dan berlatih soal ini ? Ayo lihat dulu Soal Matematika lainnya


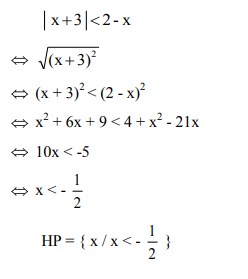

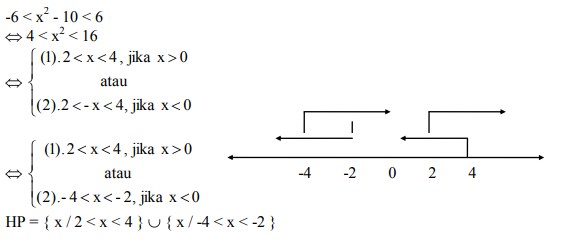





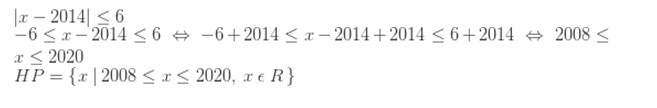
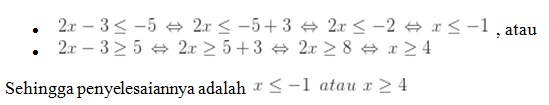


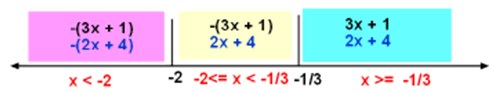
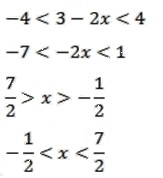

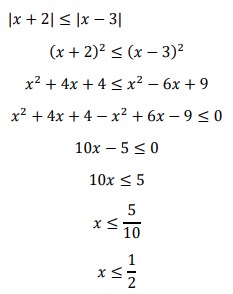
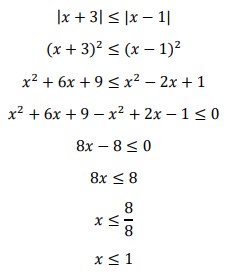
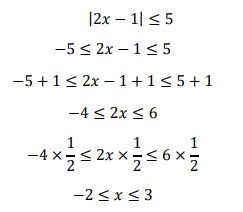
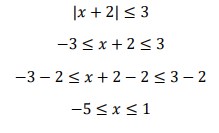


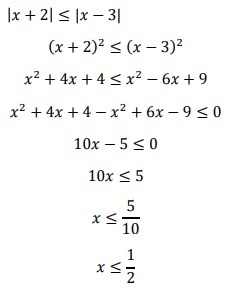
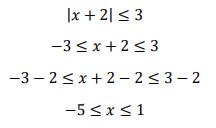


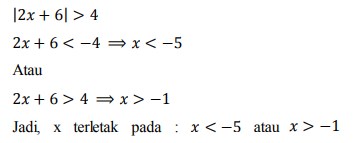
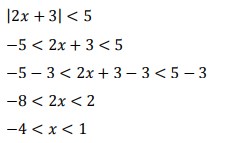

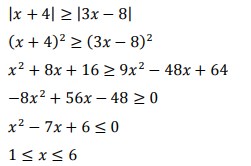



3x-2|≤ 5
hpnya itu saya rasa kurang tepat
MAKASIH YA KAK SANGAT MEMBANTU
makasih kak atas Contoh Soal Pertidaksamaan Nilai Mutlak dan Jawaban sangat membantu.
Kak tolong bantu saya ngerjain tugas ini plissss
X – 8 lebih kecil dari 17
bantu menjawab ya (maaf kalau salah)
|x – 8| < 17
= -9 < x < 25
x-8<17
-17<x-8<17
-17+8<x<17+8
-9<x<25
maka HP xI-9<x<25
Satu lagi kak 2x – 3 lebih besar + 6
bantu menjawab ya (maafkalau salah)
|2x-3| > 6
HP { x, x 9/2}
x > 9/2 atau x < -3/2
Kaka tolong bantu 🙏
[2x-1]>[×-3]
SusahNgerti
|x-1|<2|x-3| bantu jawab yaa ka tolong
|x2-5|>4 bantu jawab ka
3x-4>4x+20 tolong dong kakak caranya?🙇
|3x+5| ≤ |2x-1| Gimana caranya? tolong bntu🙏
2×+1 < 2×-3 :
Kaka tolong giman caranya
Himpunan penyelesaian dari pertidaksamaan
-5(x-1)<2-6(x+1)
Himpunan penyelesaian dari pertidaksamaan nilai mutlak berikut
|×-3|<2|×-3|+2
Kakk tolong saya tidak bisa menjawab soal
. Carilah himpunan penyelesaian dari |3X+4|>5
Jadi nilai x yang memenuhi adalah x < –1/3 atau x > 3
Himpunan penyelesaian dari pertidaksamaan nilai mutlak |x – 5| <2 adalah ..bntu jwb y ka)
1.3x+6≤15
2.4x-8≥8
3.3+2x≤16
Bantuin yaa😊
Himpunan penyelesaian dari pertidaksamaan nilai mutlak
|3x-2|<x+4
|4x-1|≥|3x-6|
Selesaikan pertidaksamaan berikut ini
1.2/x <5
2.1/3x_20
Mohon bantuannya kak
Pliss🙏🙏
Tentukan penyelesaian pertidaksamaan!
|X+5| ≥ 2X-1 toloong dijawab🙏 terimakasih
|x+3|>|x-2|=…
kak mohon bantuannya, saya sudah coba tapi ga ketemu ketemu dan lihat jawaban di web lain gak paham.
|x²-x-1| > 1
[3×+4]/2>5
Tolong bantu yah kj
tentukan hp dari perdidaksamaan berikut
|4x-6| <3x+4
|x – 5|² < 3|x – 5| – 2. X=?
Ini gmana ya? mohon bantuannya 🙏
kak tolong bantu jawab..plisss
bentuk sederhana |x+5| – |x-3| untuk nilai -5<x<3
tolong dong ka.
[x+3]<[2x-4]
Kak bantuin dong
|x-2|+3x-1|≥1
himpunan penyelesaian dari pertidaksamaan
5x+2>x-6
|1-2×|<1
____
X
3|x| < |x-1|+5
tolong dong kak
himpunan penyelesaian dari pertidaksamaan
|x-2|<3|x+7|
x + 3
x² − 4
≥ 0