Contoh Soal Faktorial dan Jawaban – Pada matematika, faktorial dari bilangan asli n adalah hasil perkalian antara bilangan bulat positif yang kurang dari atau sama dengan n. Faktorial ditulis sebagai n! dan disebut n faktorial.

Di dalam matematika faktorial biasanya digunakan untuk menghitung jumlah atau banyaknya susunan objek, yang bisa dibentuk dari sekumpulan angka tanpa harus memerhatikan bagaimana urutannya. Faktorial adalah hasil kali bilangan asli berurutan dari 1 sampai dengan n.
Faktorial dari bilangan asli n adalah hasil perkalian antara bilangan bulat positif yang kurang dari atau sama dengan n. Faktorial ditulis sebagai n! dan disebut n faktorial, tanda (!) disebut dengan notasi faktorial.
Sehingga kita dapat menarik kesimpulan bahwa:
Jika n bilangan asli maka n faktorial (n!) didefinisikan dengan :
n! = n x (n-1) x (n-2) x (n-3) x …. x 3 x 2 x 1
Dari definisi itu, maka kita juga memeroleh:
n! = n(n-1)!
Nilai dari 1! = 1. Oleh karena itu, untuk n = 1, diperoleh:
1! = 1(1-1)!
1! = 1
Jadi, untuk 0! bernilai 1. 0! = 1 Sebagai contoh, 7!
bernilai 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5040
Contoh lainnya :
0! = 1
1! = 1
2! = 1 × 2 = 2
3! = 1 × 2 × 3 = 6
4! = 1 × 2 × 3 × 4 = 24
5! = 1 × 2 × 3 × 4 × 5 = 120
6! = 1 × 2 × 3 × 4 × 5 × 6 = 720
7! = 1 × 2 × 3 × 4 × 5 × 6 × 7 = 5040
8! = 1 × 2 × 3 × 4 × 5 × 6 × 7 × 8 = 40320
9! = 1 × 2 × 3 × 4 × 5 × 6 × 7 × 8 × 9 = 362880
10! = 1 × 2 × 3 × 4 × 5 × 6 × 7 × 8 × 9 × 10 = 3628800
Berikut ini adalah contoh soal faktorial untuk kamu pelajari persiapan ulangan harian dan melatih kemampuan matematika kamu yang berjumlah 20 butir soal.
1 – 10 Contoh Soal Faktorial dan Jawaban
1. Hitunglah nilai dari:
Jawaban :
2. Tentukan nilai dari:
a. 8P3
b. 4P4
Jawaban :
3. Tentukan nilai n bila (n – 1)P2 = 20.
Jawaban :
4. Berapa banyak kata dapat disusun dari kata:
a. AGUSTUS
b. GAJAH MADA
Jawaban :
5. Berapa banyak bilangan 7 angka yang dapat disusun dari angka-angka:
a. 4, 4, 4, 5, 5, 5, dan 7
b. 2, 2, 4, 4, 6, 6 dan 8
Jawaban :
Simak Juga : Relasi dan Fungsi Pilihan Ganda
6. Pada rapat pengurus OSIS SMA X dihadiri oleh 6 orang yang duduk mengelilingi sebuah meja bundar. Berapakah susunan yang dapat terjadi?
Jawaban :
P(siklis) = (6 – 1)! = 5! = 5 × 4 × 3 × 2 × 1 = 120
7. Hitunglah nilai dari:
Jawaban :
8. Dalam pelatihan bulutangkis terdapat 10 orang pemain putra dan 8 orang pemain putri. Berapakah pasangan ganda yang dapat diperoleh untuk:
a. ganda putra
b. ganda putri
c. ganda campuran
Jawaban :
9. Berapa banyaknya nomor telepon yang terdiri dari 7 angka dapat dibuat dengan 4 digit awalnya adalah 0812, tiga digit sisanya saling berbeda dan bukan merupakan bilangan-bilangan 0, 3, atau 5, serta digit terakhirnya bukan angka 9 adalah…
Jawaban :
10. Hitunglah nilai dari:
a) 3! x 4!
b) 7! / (4! 3!)
Jawaban :
11 – 20 Contoh Soal Faktorial dan Jawaban
11. Benar atau salahkah pernyataan berikut.
a) 6! x 3! = 9!
b) 5! – 5! = 0!
c) 7! / 3! = 4!
d) 5! + 3! = 8!
e) 6! / 3! = 2!
Jawaban :
12. Tulislah dalam notasi faktorial:
Jawaban :
13. Hitunglah nilai n yang memenuhi:
14. Hitunglah nilai P(5, 2)
Jawaban :
15. Jika n! / (n – 2)! = 20, maka nilai n = …
A. 6
B. 5
C. 4
D. 3
E. 2
Jawaban : B
Pembahasan
n2 – n = 20
n2 – n – 20 = 0
(n – 5) (n + 4) = 0
n = 5 atau n = -4 (tidak mungkin negatif)
Lihat Juga : Soal Peluang Pilihan Ganda dan Jawaban
16. n+1P3 = nP4 = maka n = …
A. 2
B. 3
C. 4
D. 5
E. 6
Jawaban : D
Pembahasan
n+1P3 = nP4
(n + 1) . n . (n – 1) ! = n . (n – 1) . (n – 2) . (n – 3) !
(n + 1) = (n – 2) . (n – 3)
n + 1 = n2 – 5n + 6
n2 – 6n + 5 = 0
(n – 5) (n – 1) = 0
n = 5 atau n = 1
17. Sebuah bangku panjang hanya dapat diduduki oleh 5 orang. Banyak cara 8 orang menduduki bangku sama dengan…
A. 6720
B. 336
C. 40
D. 36
E. 24
Jawaban : A
Pembahasan
Diketahui:
n = 8
k = 5
Ditanya: 8P5 = …
8P5 = 8! / (8 – 5)! = 8 . 7 . 6 . 5 . 4 . 3! / 3! = 8 . 7 . 6 . 5 . 4 = 6720
18. Banyak permutasi atau susunan yang berbeda 6 orang duduk mengelilingi suatu meja bundar adalah…
A. 720
B. 120
C. 24
D. 12
E. 6
Jawaban : B
Pembahasan
Banyak susunan melingkar = (n – 1)! = (6 – 1)! = 5 ! = 5 . 4. 3 . 2 . 1 = 120
19. Misal 6 orang akn duduk mengelilingi sebuah meja bundar. Jika ada dua orang tertentu yang harus duduk sebelah menyebelah, maka banyak susunan yang berbeda yang mungkin sama dengan…
A. 96
B. 48
C. 24
D. 14
E. 12
Jawaban : C
Pembahasan:
Banyak susunan = (n – 2)! karena ada 2 orang yang sebelah menyebelah
Banyak susunan = (6 – 2) ! = 4! = 4 . 3. 2 . 1 = 24
20. Banyak permutasi dari huruf yang terdapat pada kata SAMASAJA = …
A. 1680
B. 840
C. 40
D. 210
E. 105
Jawaban : B
Pembahasan
Diketahui
n1 = 2 (2 huruf S sama)
n2 = 4 (4 huruf A sama)
Ditanya:
8P2,4 = . . .
8P2,4 = 8! / 2! . 4! = 8 . 7 . 6 . 5 . 4! / 2!. 4! = 8 . 7 . 6 . 5/2 = 840
Sudah selesai membaca dan berlatih soal ini ? Ayo lihat dulu Soal Matematika lainnya

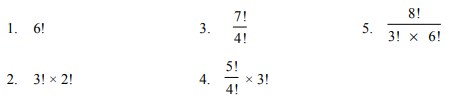
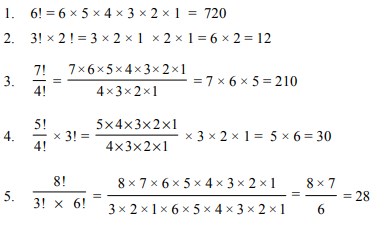
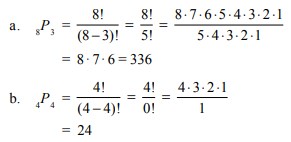
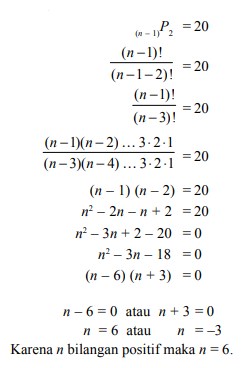



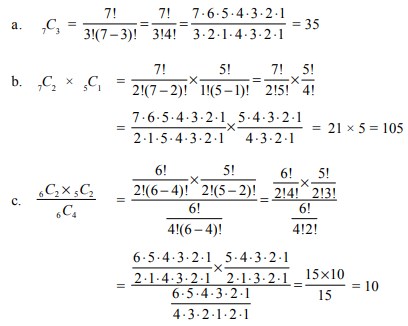



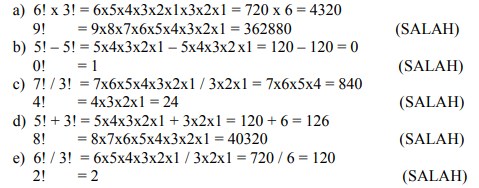

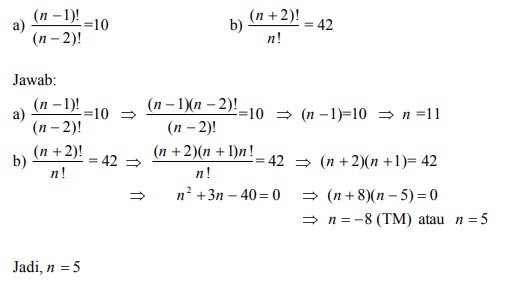




Berapa nilai dari bentuk (3!+5)!
= ((3 × 2 × 1) + 5)!
= (6 + 5)!
= 11!
= 11 x 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1
= 39916800