25+ Soal Operasi Hitung Bentuk Aljabar dan Jawaban [Update]

Contoh Soal Operasi Bentuk Aljabar dan Jawaban – Aljabar dapat didefinisikan sebagai manipulasi dari simbol – simbol. Teknik memasukkan suatu simbol, misalnya 𝑥, untuk melambangkan (mempresentasikan) suatu bilangan yang tidak diketahui di dalam menyelesaikan berbagai permasalahan. Bentuk Aljabar adalah suatu bentuk matematika yang dalam penyajiannya memuat huruf- huruf untuk mewakili bilangan yang belum diketahui.

Unsur – unsur pada bentuk aljabar :

Variabel : Pada bentuk aljabar 2𝑥, −3𝑝 + 7, huruf 𝑥 dan 𝑝 disebut variabel. Variabel adalah lambang pengganti suatu bilangan yang belum diketahui nilainya dengan jelas. Variabel disebut juga peubah. Variabel biasanya dilambangkan dengan huruf kecil 𝑎, 𝑏, 𝑐, … 𝑧.

Konstanta : Bilangan 7 pada bentuk aljabar di atas disebut konstanta. Konstanta adalah suku dari suatu bentuk aljabar yang berupa bilangan dan tidak memuat variabel.

Koefisien : adalah banyaknya variabel. Pada bentuk aljabar di atas 2 dan -3 merupakan koefisien.

Suku : sejenis dan Suku tak sejenis Suku adalah variabel beserta koefisiennya atau konstanta pada bentuk aljabar yang dipisahkan oleh operasi jumlah atau selisih

1 – 10 Contoh Soal Operasi Bentuk Aljabar dan Jawaban

1. Tentukan variabel dari bentuk aljabar 25𝑥 + 12 !

Jawaban : 

Variabel dari 25𝑥 + 12 adalah 𝑥

2. Tentukan konstanta pada bentuk aljabar 4𝑥² − 6𝑥𝑦 + 8𝑥 − 10𝑦 − 12 !

Jawaban : 

Konstanta dari 4𝑥² − 6𝑥𝑦 + 8𝑥 − 10𝑦 − 12 adalah −12

3. Tentukan koefisien 𝑝 pada bentuk aljabar: 6𝑝² − 𝑝 − 5 !

Jawaban : 

Koefisien 𝑝 dari 6𝑝² − 𝑝 − 5 adalah −1

4. Sebutkan suku-suku sejenis dari bentuk aljabar 6𝑎 + 8𝑎𝑏 + 3𝑎𝑏 + 6𝑏 !

Jawaban : 

Suku-suku sejenis dari 6𝑎 + 8𝑎𝑏 + 3𝑎𝑏 + 6𝑏 adalah 8𝑎𝑏 dan 3𝑎𝑏

5. Tentukan hasil penjumlahan bentuk aljabar (4𝑥 + 19𝑦 − 25𝑧) dengan (34𝑥 − 12𝑦 − 56𝑧) !

Jawaban : 

Hasil penjumlahan bentuk aljabar (4𝑥 + 19𝑦 − 25𝑧) dengan (34𝑥 − 12𝑦 − 56𝑧)

(4𝑥 + 19𝑦 − 25𝑧) + (34𝑥 − 12𝑦 − 56𝑧) = 38𝑥 + 7𝑦 − 81𝑧

6. Tentukan hasil pengurangan bentuk aljabar (4𝑥 − 2𝑦 − 7) dengan (−3𝑥 + 5𝑦 + 3) !

Jawaban : 

Hasil pengurangan bentuk aljabar (4𝑥 − 2𝑦 − 7) dengan (−3𝑥 + 5𝑦 + 3)

(4𝑥 − 2𝑦 − 7) −(−3𝑥 + 5𝑦 + 3) = 7𝑥 − 7𝑦 − 10

7. Tentukan hasil perkalian bentuk aljabar dari 8(4y – 11) !

Jawaban : 

Hasil perkalian bentuk aljabar dari 8(4y – 11)

8(4y – 11) = 32𝑦 − 88

8. Tentukan hasil perkalian bentuk aljabar dari (2𝑥 + 3)(4𝑥 − 5) !

Jawaban : 

Hasil perkalian bentuk aljabar dari (2𝑥 + 3)(4𝑥 − 5)

(2𝑥 + 3)(4𝑥 − 5)   = 8𝑥² − 10𝑥 + 12𝑥 − 15

= 8𝑥² + 2𝑥 − 15

9. Tentukan hasil pembagian bentuk aljabar dari (6𝑥² − 8𝑥 − 14) dibagi dengan (3𝑥 − 7) !

Jawaban : 

Hasil pembagian bentuk aljabar dari (6𝑥² − 8𝑥 − 14) dibagi dengan (3𝑥 − 7)

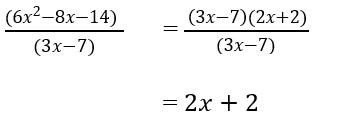
10. Sederhanakan bentuk aljabar berikut dari

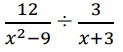
Jawaban : 

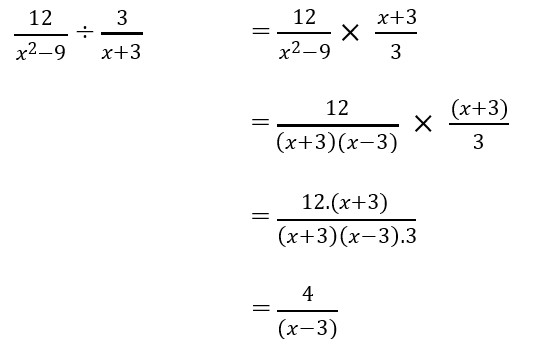
11 – 25 Soal Operasi Bentuk Aljabar dan Jawaban

11. Sederhanakan bentuk aljabar berikut dari

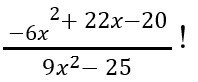
Jawaban : 

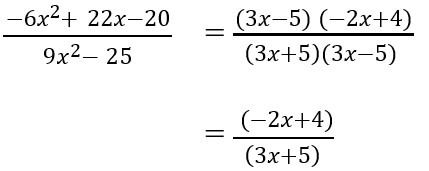
12. Sederhanakan bentuk aljabar berikut

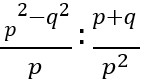
Jawaban : 

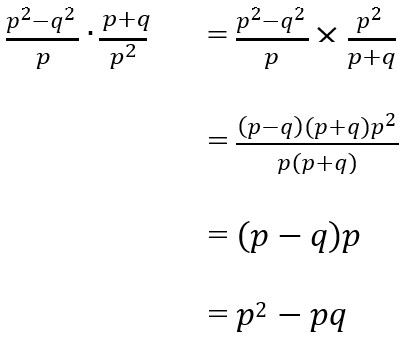
13. Perhatikan foto berikut ini!

Dapatkah kamu menyatakan banyak bawang putih, bawang merah dan buah pisang ke dalam bentuk aljabar ? Tuliskan !

Jawaban : 

banyak bawang putih, bawang merah dan buah pisang ke dalam bentuk aljabar adalah 𝑥 + 𝑦 + z

14. Tentukan variabel, koefisien dan konstanta pada bentuk aljabar di bawah ini!

a. 6𝑥

b. −𝑎 + 8𝑏 − 10𝑐 − 11

c. 𝑗² − 2𝑘 − 15𝑚 + 6

Jawaban : 

15. Tentukan banyak suku pada bentuk aljabar dibawah ini!

a. 7𝑧

b. 8𝑥 + 𝑦 + 6𝑧

c. 7𝑠 + 10𝑡 + 𝑢 + 6

Jawaban : 

16. Kelompokkan suku – suku berikut ini berdasarkan suku sejenisnya!

a. 𝑘, 6𝑚, 4𝑘, 7𝑚

b. 10𝑎² 𝑏, 5𝑎𝑏², −3𝑎²𝑏, −𝑎𝑏²

c. 19𝑎, 10𝑎², 6𝑎, 6𝑎²

Jawaban : 

17. Pak Dani membeli 20 sak semen, 100 bata merah dan 12 batang besi, sudah dipergunakan untuk membangun rumah 5 sak semen, 50 bata merah dan 6 batang besi , karena diperkirakan kurang, Pak Dani membeli lagi 8 sak semen, 30 bata merah dan 10 batang besi. Berapakah jumlah bahan bangunan Pak Dani sekarang ?

Jawaban : 

Diketahui :

Terdapat 20 sak semen, 100 bata merah dan 12 batang besi, sudah dipergunakan untuk membangun rumah 5 sak semen, 50 bata merah dan 6 batang besi , karena diperkirakan kurang, Pak Dani membeli lagi 8 sak semen, 30 bata merah rumah dan 10 batang besi.

Ditanyakan : jumlah bahan bangunan Pak Dani sekarang ?

Jawab :

Jadi jumlah bahan bangunan Pak Dhani sekaranga adalah 23𝑥 + 80𝑦 + 16𝑧 yaitu 23 sak semen, 80 bata merah dan 16 batang besi

Simak Juga : Contoh Soal Operasi Bilangan Bulat

18. Bu Ani adalah pemilik toko baju. Dia mendapat pesanan sebanyak 25 kemeja, 14 celana, dan 25 rok. Persedian baju yang dimiliki Bu Ani adalah 7 kemeja, 15 celana, dan 20 rok. Berapakah kekurangan baju yang harus disediakan Bu Ani agar pesanan pelanggan terpenuhi?

Jawaban : 

Diketahui :

Bu Ani mendapat pesanan sebanyak 25 kemeja, 16 celana, dan 25 rok. Persedian baju yang dimiliki Bu Ani adalah 7 kemeja, 15 celana, dan 20 rok.

Ditanyakan :

Kekurangan barang yang harus disediakan Bu Ani agar pesanan pelanggan terpenuhi?

Jawab :

Jadi kekurangan barang yang harus disediakan Bu Ani agar pesanan terpenuhi adalah 18 kemeja, 1 celana dan 5 rok

19. Tentukan pejumlahan bentuk aljabar berikut ini!

a. (7𝑎 + 8𝑏) + (9𝑎 + 8𝑏)

b. (17𝑠 + 55𝑠 + 11𝑠) + (26𝑢 + 48𝑢 + 11𝑢)

c. (10𝑎² + 18𝑎𝑏² + 𝑏²) + ((−𝑎²) + 10𝑎𝑏² − 11𝑏²

Jawaban : 

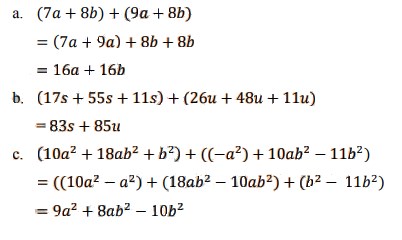
20. Tentukan pengurangan bentuk aljabar berikut ini !

a. (6𝑘 − 8𝑙) − (𝑘 + 11𝑙)

b. (17𝑠 + 55𝑠 + 11𝑠) − (26𝑢 + 48𝑢 + 11𝑢)

c. (10𝑝² + 18𝑞𝑟² + 𝑞²) − ((−𝑝²) + 10𝑞²𝑟² − 11𝑞²

Jawaban : 

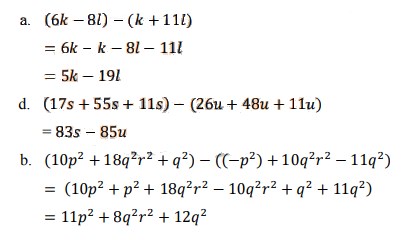
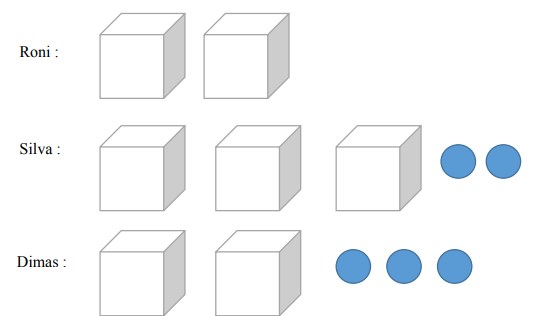
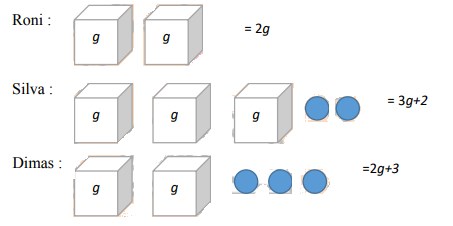
21. Roni, Silva dan Dimas masing – masing mempunyai kotak berisi sejumlah koin yang isinya sama banyak dan beberapa koin berada di luar kotak, seperti terlihat pada gambar di bawah ini. Bagaimana bentuk aljabar untuk menyatakan banyaknya koin yang dimiliki oleh masing –masing dari mereka ?

Keterangan : g menunjukkan banyaknya jumlah koin dalam kotak

Jawaban : 

Diketahui :

Roni memiliki 2 kotak, Silva memiliki 3 kotak dan 2 koin , Dimas memiliki 2 kotak dan 3 koin g menunjukkan banyaknya jumlah koin dalam kotak

Ditanya:

bentuk aljabar untuk menyatakan banyaknya koin masing –masing dari mereka

Jawab :

22. Tentukan penjumlahan bentuk aljabar berikut :

a. 12𝑥 + 12𝑦 − 5𝑧 dengan −11𝑥 − 10𝑦 + 4𝑧

b. −6𝑚 + 4𝑛 − 2 dengan −8𝑚 − 7𝑛 + 5

Jawaban : 

23. Tentukan pengurangan bentuk aljabar berikut :

a. 5𝑥 + 4𝑦 − 8 dari 2𝑥 + 5𝑦 − 10

b. 4𝑚² + 6𝑚𝑛 − 8𝑛

2 dari −13𝑚² + 6𝑚𝑛 − 10𝑛²

Jawaban : 

24. Perhatikan gambar berikut ini :

Hari ini Siska dan Dyah bermain kelereng bersama. Siska membawa 3 kotak berisi kelereng, 1 toples berisi kelereng dan 2 kelereng di luar kotak dan toples. Sedangkan Dyah membawa 1 kotak berisi kelereng, 1 toples berisi kelereng dan 2 kelereng di luar kotak dan toples.

a) Tentukan jumlah dari kelereng yang di bawa oleh Siska dan Dyah dalam bentuk aljabar ! Asumsikan jumlah kelereng setiap kotak dan setiap toples masing – masing adalah sama.

b) Tentukan variabel, konstanta, koefisien dan suku dari bentuk aljabar yang kamu peroleh !

Jawaban : 

Diketahui :

Siska membawa 3 kotak berisi kelereng, 1 toples berisi kelereng dan 2 kelereng diluar kotak dan toples. Sedangkan Dyah membawa 1 kotak berisi kelereng, 1 toples berisi kelereng dan 2 kelereng di luar kotak dan toples.

Asumsi : Jumlah kelereng setiap kotak dan setiap toples masing – masing adalah sama.

Ditanyakan :

a. Tentukan bentuk aljabar dari kelereng yang dibawa oleh Siska dan Dyah!

b. Tentukan unsur-unsur dari bentuk aljabar yang kamu peroleh ?

Jawab :

Misal :

𝑥 = menyatakan banyak kelereng dalam satu kotak

𝑦 = menyatakan banyak kelereng dalam satu toples

a. 3𝑥 + 𝑦 + 2 + 𝑥 + 𝑦 + 2

= 3𝑥 + 𝑥 + 𝑦 + 𝑦 + 2 + 2

= 4𝑥 + 2𝑦 + 4

Jadi bentuk aljabar dari kelereng yang dibawa oleh Siska dan Dyah adalah 4𝑥 + 2𝑦 + 4 .

b. Variabel : 𝑥 dan 𝑦

Konstanta : 4

Koefisien :4 dan 2

Suku : terdiri dari 3 suku yaitu 4𝑥, 2𝑦 dan 4

25. Ibu Lusi mempunyai 10 keranjang berisi penuh buah nanas di rumah, kemudian Ia memanen buah nanas lagi di kebun. Sekarang Bu Lusi mempunyai keranjang berisi penuh buah nanas sebanyak 19 keranjang dan 7 buah nanas. Keesokan harinya pedagang buah datang ke rumah Bu Lusi untuk membeli 15 keranjang buah nanas. Kemudian Bu Lusi mengambil 5 buah nanas untuk membuat selai nanas.

a. Tentukan hasil panen buah nanas dari kebun Bu Lusi ?

b. Berapa total keseluruhan keranjang buah nanas milik Bu Lusi sekarang ?

Jawaban : 

Diketahui:

-10 keranjang berisi penuh buah nanas

-Total keranjang setelah panen sebanyak 19 dan 7 buah nanas

-Pedagang buah membeli 15 keranjang buah nanas dan 5 buah nanas.

Ditanya:

a. Hasil panen buah nanas dari kebun Bu Lusi ?

b. Total keseluruhan keranjang buah nanas milik Bu Lusi sekarang?

Jawab

Misal x menyatakan banyak buah nanas dalam satu keranjang

a. Hasil panen = Jumlah keranjang setelah panen + jumlah kerangjang sebelum panen

= 19𝑥 − 10𝑥 + 7

= 9𝑥 + 7

Jadi hasil panen buah nanas dari kebun Bu Lusi adalah 9𝑥 + 7

b. Total keseluruhan keranjang buah nanas milik Bu Lusi sekarang

= 10𝑥 + 9𝑥 + 7 − 15𝑥 − 5

= 10𝑥 + 9𝑥 − 15𝑥 + 7 − 5

= 4𝑥 + 2

Jadi, Total keseluruhan keranjang buah nanas milik Bu Lusi sekarang adalah 4𝑥 − 2

Sudah selesai membaca dan berlatih Soal Operasi bentuk Aljabar ini ? Ayo lihat dulu Soal Matematika lainnya

Posting terkait:

Contoh Soal Barisan dan Deret Aritmatika [Update 50 Butir]

Contoh Soal Lingkaran Kelas 8 SMP dan Jawaban [Update]

65+ Contoh Soal Limit Fungsi Aljabar dan Jawaban [Update]