Pada dasarnya dalam menyelesaikan segitiga adalah mencari panjang setiap sisinya dan semua sudutnya. Aturan sinus digunakan ketika kita diberikan a) dua sudut dan satu sisi, atau b) dua sisi dan tidak termasuk sudutnya. Aturan cosinus digunakan ketika kita diberikan a) tiga sisi atau b) dua sisi dan termasuk sudutnya.

1 – 10 Soal Aturan Sinus dan Cosinus dan Jawaban
1. Diketahui segitiga ABC, dengan panjang AC = 25 cm, sudut A = 60°, dan sudut C = 75° jika sin 75° = 0,9659, tentukan panjang BC dan AB!
Jawaban :
Buat sketsa gambarnya :
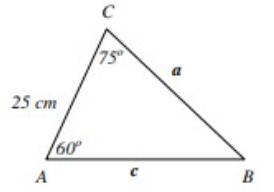
Maka besar sudut B adalah
∠ B = 180° – (∠ A + ∠ C)
∠ B = 180° – (60° + 75°)
∠ B = 180° – 135°
∠ B = 45°
Sehingga

2. Pada segitiga ABC, sisi AC = 16 cm, AB = 8 √2 cm, sudut B = 45°. tentukan sudut-sudut segitiga ABC yang lainnya!
Jawaban :
3. Diketahui segitiga ABC, dengan panjang BC = 4 cm, AC = 6 cm dan sudut C = 60°, tentukan panjang sisi AB!
Jawaban :
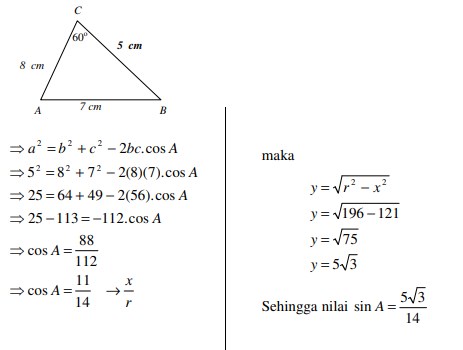
4. Diketahui segitiga ABC, dengan AB = 7 cm, AC = 8 cm, BC = 5 cm, tentukan sin A!
Jawaban :
5. Tentukan luas segitiga ABC, jika diketahui AB = 15 cm, BC = 10 cm, ∠ B = 30°!
Jawaban :
Simak Juga : Soal Persamaan Trigonometri
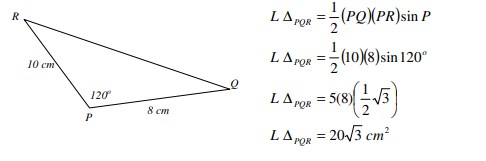
6. Tentukan luas segitiga PQR, jika diketahui ∠P = 120°, panjang PR = 10, PQ = 8 adalah. . .
Jawaban :
7. Terdapat segitiga PQR, dengan panjang PQ = 6 cm, QR = 8 cm, dan PR = 12 cm. Maka tentukanlah besar sudut P, Q dan R!
Jawaban :
Dik :
PQ = 6 cm
QR = 8 cm
PR = 12 cm
Dit : besar sudut P, Q dan R?
Jawaban :
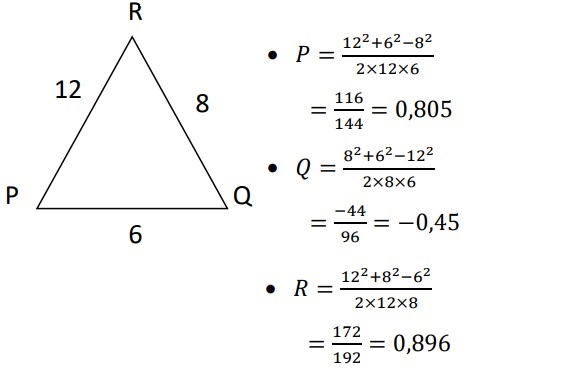
8. Luas segi 12 beraturan dengan jari-jari lingkaran luar 8 cm adalah….
A. 192 cm2
B. 172 cm2
C. 162 cm2
D. 148 cm2
E. 144 cm2
Jawaban :
9. Diketahui bahwa segitiga ABC memiliki sudut A=60 0 dan sudut B=300 dengan garis AB = 140 dan AC = 80, tentukan berapa panjang garis CB!
Jawaban :
10. Dengan ketentuan Sudut CAB = 30,BCA = 90. maka tentukan garis AC!
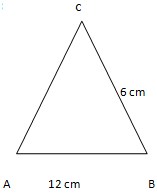
Jawaban :
11 – 20 Soal Aturan Sinus dan Aturan Cosinus dan Jawaban
11. Diketahui segitiga PQR siku – siku di Q dengan <P = 300 dan panjang sisi PQ = 4 cm , hitunglah panjang PR!
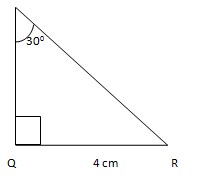
Jawaban :
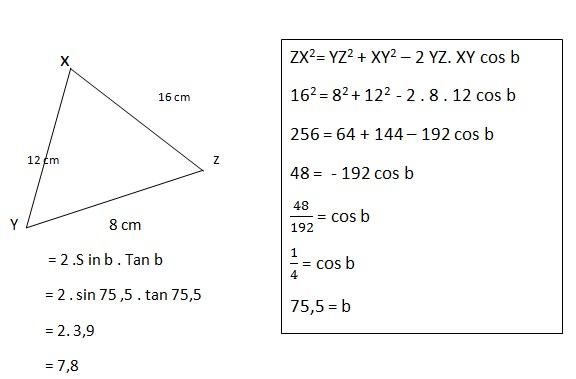
12. Sebuah segitiga XYZ dengan panjang XY = 12 , YZ = 8 , ZX= 16 . jika diketahui B merupakan sudut yang terbentuk antara sisi YX dan YZ . Maka nilai 2 Sin B. Tan B adalah…
Jawaban :
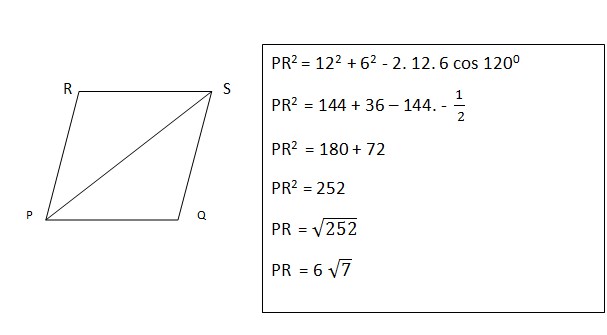
13. Sebuah jajar genjang PQRS dengan panjang QR = 12 cm dan RS = 6 cm sudut q = 1200, maka panjang garis PR adalah…
Jawaban :
14. Hitunglah Panjang tali busur pada juring PKL = 1350 dengan jari – jari 10 cm!
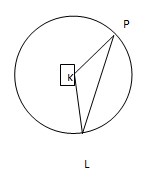
Jawaban :
PL2 = 102 + 102 – 2 . 10 . 10 cos 135
PL2 = 100 + 100 – 200 . cos 45
PL2 = 200 – 200 . ½ √2
PL2 = 200 + 100 √2
PL2 = 200 + 100 . 1,4
PL2 = 200 + 140
PL2 = 340
PL = 2√85
15. Perhatikan segitiga berikut :
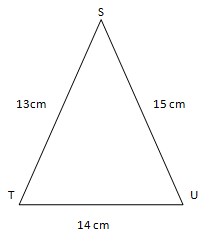
Tentukanlah berapa Luas dari segitiga diatas!
Jawaban :
Baca Juga : Soal Ujian Matematika Kelas 10 SMA Semester 1 K.13
16. Hitunglah luas segitiga ABC, dengan panjang sisi-sisinya a = 3 m, b= 8 m, c = 9 m adalah…
Jawaban :
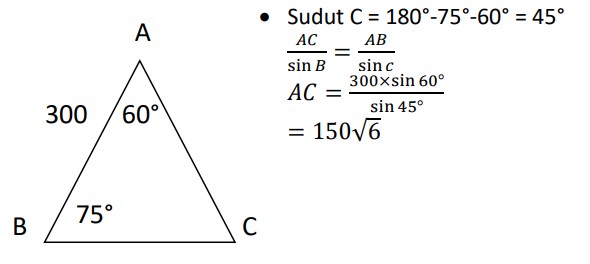
17. Diketahui segitiga MAB dengan AB = 300 cm sudut MAB = 60° dan sudut ABC = 75°, maka panjang sisi AC!
Jawaban :
Dik :
AB = 300 cm
Sudut A = 60°
Sudut B = 75°
Dit : panjang sisi AC?
18. Diketahui segitiga ABC, ∠𝛼 = 300, ∠𝛽 = 450 dan a = 20 cm. Tentukanlah besar sudut 𝛾, panjang sisi b dan panjang sisi c!
Jawaban :
Diketahui:
∆ ABC dengan ∠𝛼 = 300, ∠𝛽 = 450 dan a = 20 cm
Dalam ∆ ABC, 𝛼 + 𝛽 + 𝛾 = 180°
30° + 45° + 𝛾 = 180°
𝛾 = 150°
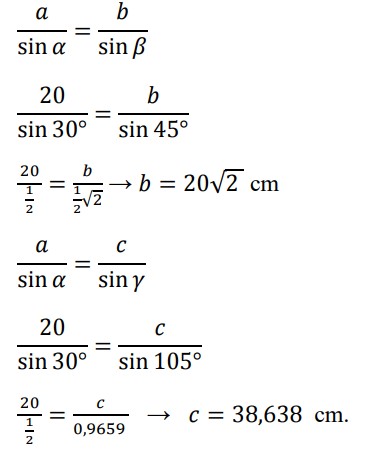
19. Pada ΔABC berikut diketahui tiga buah unsur. Hitunglah sisi yang belum diketahui (teliti sampai 2 tempat desimal)
a) a = 5, b = 7 dan ∠ C = 68o
b) a = 5, c = 6 dan ∠ B = 52o
Jawaban :
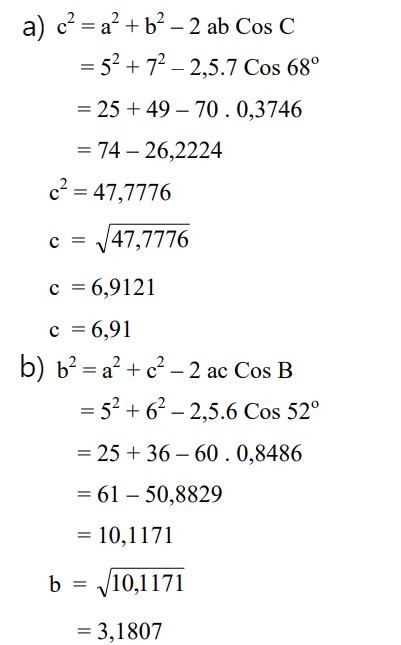
20. Sebuah tiang bendera berdiri tegak diatas pada sebuah gedung yang bertingkat dari suatu temat yang berada diatas tanah, titik angkal tiang bendera terlihat dengan sudut elevasi 66 dan titik ujung tiang bendera terlihat dengan sudut elevasi 70. Jika jarak horizontal dari titik pengamatan ke titik tepian gedung sama dengan 10 meter. Berapakah tinggi tiang bendera tersebut.
Jawaban :
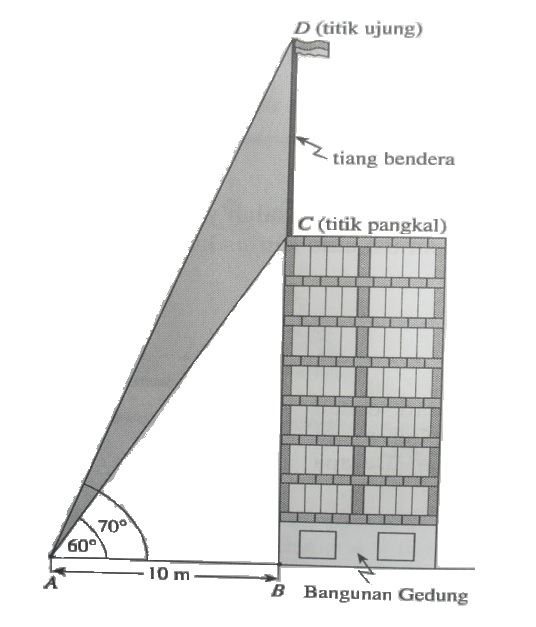
Tinggi tiang bendera itu adalah CD, misalkan CD = h meter Dalam ∆ ABC berlaku aturan sinus, sehingga di peroleh :

Jadi, tinggi tiang bendera itu adalah 10. 15 meter
Sudah selesai membaca dan berlatih soal ini ? Ayo lihat dulu Daftar Soal Matematika lainnya



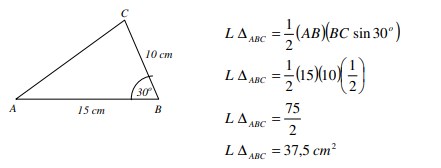

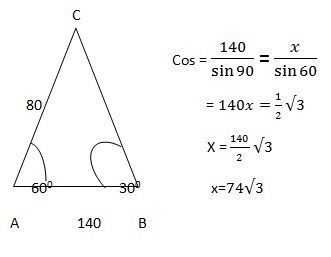
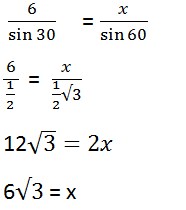
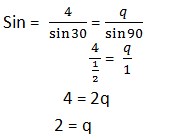
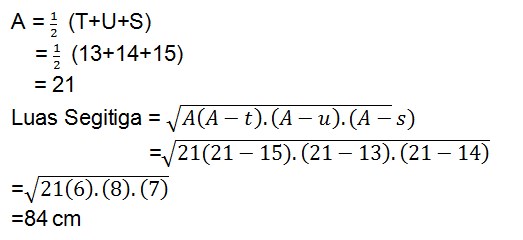




Berkomentarlah yang positif tinggalkan yang negatif