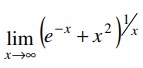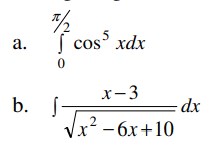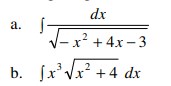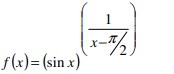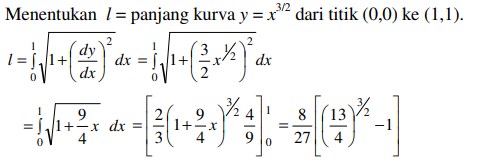Contoh Soal Kalkulus Dasar dan Jawaban [+Pembahasan]

Contoh Soal Kalkulus Dasar dan Jawaban [+Pembahasan] – Kalkulus Merupakan Metode ini didasarkan pada turunan dan fungsi, dengan metode yang didasarkan pada penjumlahan perbedaan yang sangat kecil. Kedua jenis utama adalah kalkulus diferensial dan kalkulus integral.

Kalkulus (bahasa Latin: calculus, artinya “batu kecil”, untuk menghitung) adalah cabang ilmu matematika yang mencakup limit, turunan, integral, dan deret tak terhingga.

Kalkulus adalah ilmu yang mempelajari perubahan, sebagaimana geometri yang mempelajari bentuk dan aljabar yang mempelajari operasi dan penerapannya untuk memecahkan persamaan.

Materi dari kalkulus adalah sebagai berikut :

• Sistem Bilangan, Pertaksamaan dan Koordinat Kartesius
• Fungsi dan Limit
• Turunan
• Penggunaan Turunan
• Integral
• Penggunaan Integral
• Fungsi-Fungsi Transenden

1 – 10 Soal Kalkulus Dasar beserta Jawaban

1. Diketahui daerah D dibatasi kurva y = x , garis y =1 , garis x = 4 .

a. Gambarkan daerah D

b. Hitung luas daerah D

c. Hitung volume benda putar bila D diputar terhadap sumbu y.

Jawaban :

2. Hitunglah : 

a) turunan dari y = e^sin-1x

b) Hitunglah

Jawaban :

3. Hitung integral berikut ini : 

Jawaban :

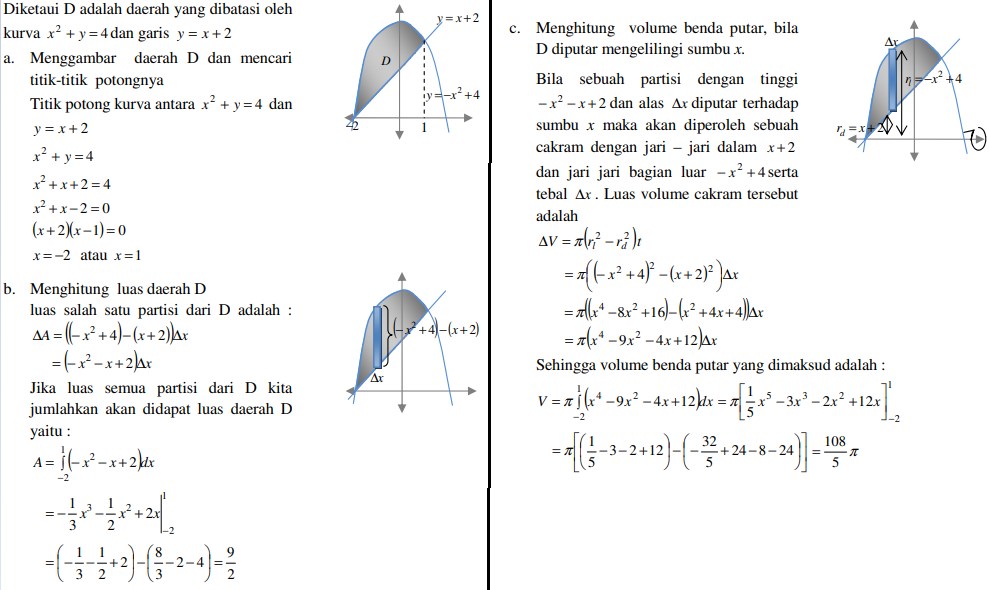
4. Diketahui D adalah daerah yang dibatasi oleh kurva x² + y = 4 dan garis y = x + 2

a. Gambarkan daerah D dan cari titik-titik potongnya

b. Hitung luas daerag D

c. Hitung volume benda putar, bila D diputar mengelilingi sumbu x

Jawaban : 

5. Bila  konstanta. Tentukan a sehingga f’ (0) = 2 adalah . . .

Jawaban : 

Simak Juga : Soal Deret Geometri Tak Hingga Pilihan Ganda [+Penyelesaian]

6. Hitung integral :

Jawaban : 

7. Diketahui suatu daerah D di kuadran I yang dibatasi oleh kurva y = 4 − x² , garis y = 3x dan sumbu y.

a. Gambarkan daerah D dan hitung luasnya

b. Hitung volume benda putar, bila D diputar terhadap garis x = 4

Jawaban : 

8. Diketahui

a) Hitunglah

b) Tentukan turunan pertama dari f (x)

Jawaban : 

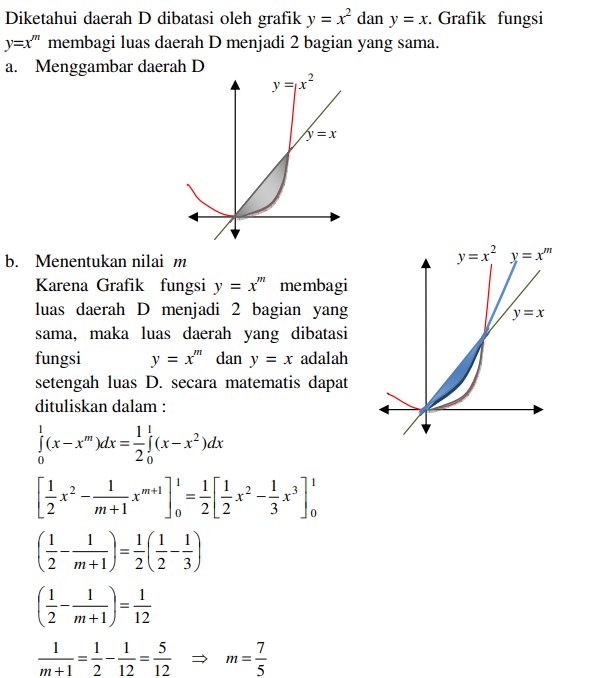
9. Diketahui daerah D dibatasi oleh grafik y = x² dan y = x. Grafik fungsi y = x^m membagi luas daerah D menjadi dua bagian yang sama.

a. Gambarkan daerah D

b. Tentukan m 

Jawaban : 

10. Tentukan panjang kurva y = x^3/2 dari titik (0,0) ke (1,1) adalah. . .

Jawaban : 

Posting terkait:

Contoh Soal Barisan dan Deret Aritmatika [Update 50 Butir]

Contoh Soal Lingkaran Kelas 8 SMP dan Jawaban [Update]

65+ Contoh Soal Limit Fungsi Aljabar dan Jawaban [Update]