Contoh Soal Persamaan Nilai Mutlak dan Jawaban – Persamaan Nilai Mutlak adalah suatu nilai (bilangan/angka) mutlak dari sebuah bilangan sehingga dapat juga dinyatakan sebagai jarak bilangan tersebut terhadap titik [0] pada garis bilangan tanpa memperhatikan arahnya.
Nilai mutlak didefinisikan jarak pada garis bilangan real antara bilangan yang dimaksud dengan dengan nol.

1 – 10 Soal Persamaan Nilai Mutlak dan Jawaban
1. Tentukan berapa nilai mutlak dari persamaan | 10 – 3 | = adalah . . .
Jawaban :
| 10 – 3 | = | 7 | = 7
2. Tentukan berapa hasil x untuk persamaan nilai mutlak | x – 6 | =10 adalah . . .
Jawaban :
Untuk menyelesaikan persamaan tersebut, terdapat dua kemungkinan hasil bilangan mutlak
| x – 6 | = 10
Solusi pertama:
x – 6 =10
x = 16
Solusi kedua:
x – 6 = -10
x = -4
Jadi, jawaban untuk persamaan ini yaitu 16 atau (-4)
3. Tentukan himpunan penyelesaian dari persamaan nilai mutlak | x + 5 | = 3
Jawaban :
Pada bentuk ini ada dua penyelesaian.
Penyelesaian pertama :
x + 5 = 3, maka x = 3 – 5 = -2
Penyelesaian kedua :
x + 5 = -3, maka x = -3 -5 = -8
Jadi, himpunan penyelesaiannya adalah {-2, -8}
4. Tentukanlah Pesamaan nilai mutlak dari | 2 x -3 | = 5 adalah . . .
Jawaban :
Pada bentuk ini ada dua penyelesaian.
Penyelesaian pertama :
2x + 3 = 5 , maka 2x = 5 – 3
2x = 2 ⇔ x = 1
Penyelesaian kedua :
2x + 3 = -5 , maka 2x = -5 -3
2x = -8 ⇔ x = -4
Jadi, himpunan penyelesaiannya adalah {-4, 1}
5. Tentukanlah Pesamaan nilai mutlak dari |3x + 4| = x – 8 adalah. . .
Jawaban :
Perhatikan bentuk aljabar di dalam tanda mutlak, yaitu 3x + 4 maka Penyelesaian persamaan nilai mutlak ini juga dibagi menjadi dua bagian.
Bagian pertama untuk batasan 3x + 4 ≥ 0 atau x ≥ -4/3
Bagian kedua untuk batasan 3x + 4 < 0 atau x < -4/3
Mari kita selesaikan :
Bagian pertama
untuk x >=-4/3
Persamaan mutlak dapat ditulis:
(3x + 4) = x – 8
3x – x = -8 – 4
2x =-12
x = -6 (tidak terpenuhi, karena batasan >= -4/3)
Bagian kedua
untuk x < -4/3
Persamaan mutlak dapat ditulis:
-(3x + 4) = x – 8
-3x – 4 = x -8
-3x – x = -8 + 4
-4x = -4
x = 1 (tidak terpenuhi, karena batasan < -4/3)
Jadi, Tidak ada Himpunan penyelesaiannya.
Simak Juga : Soal Pertidaksamaan Nilai Mutlak
6. Carilah himpunan penyelesaian dari |y + 1 | = 2y + 3 adalah . . .
Jawaban :
7. Carilah himpunan penyelesaian dari persamaan berikut | x + 1 | = 3 adalah. . .
Jawaban :
8. Selesaikan persamaan berikut :
|7 – 2x| – 11 = 14
Tentukanlah berapa nilai x adalah. . .
Jawaban :
|7 – 2x| – 11 = 14
|7 – 2x| = 14 + 11
|7 – 2x| = 25
Selesai pada persamaan diatas, maka bilangan untuk nilai mutlak x adalah sebagai berikut
7 – 2x = 25
2x = – 18
x= – 9
atau
7 – 2x = – 25
2x = 32
x = 16
Sehingga hasil akhir nilai x adalah (– 9) atau 16
9. Tentukan penyelesaian dari persamaan nilai mutlak berikut:
|4x – 2| = |x + 7|
Jawaban :
Untuk menyelesaikan persamaan diatas, menggunakan dua kemungkinan penyelesaian yaitu:
4x – 2 = x + 7
x = 3
atau
4x – 2 = – ( x + 7)
x= – 1
Jadi penyelesian persamaan |4x – 2| = |x + 7| adalah x = 3 atau x= – 1
10. Tentukan penyelesaian persamaan nilai mutlak berikut:
|3x+2|²+|3x+2| – 2=0
Tentukanlah berapa nilai x adalah. . .
Jawaban :
Penyederhanaan : |3x+2| = p
maka
|3x+2|²+ |3x+2| -2=0
p² + p – 2 = 0
(p+2) (p – 1) = 0
p+2 = 0
p = – 2 (ingat : nilai mutlak tidak negatif!)
atau
p – 1 = 0
p = 1
|3x+2| = 1
Sampai pada penyelesaian diatas, maka terdapat 2 kemungkinan jawaban untuk x, yaitu:
3x+2 = 1
3x = 1 – 2
3x = – 1
x = – 1/3
atau
– (3x+2) = 1
3x+2 = – 1
3x = – 1 – 2
3x = – 3
x = – 1
Jadi penyelesaian persamaan tersebut adalah x= – 1/3 atau x= – 1
11 – 20 Soal Persamaan Nilai Mutlak dan Jawaban
11. Tentukan himpunan penyelesaian dari persamaan nilai mutlak | x + 5 | = 3 adalah. . .
Jawaban :
Pada prinsipnya, langkah langkah penyelesaian nilai mutlak soal ini diusahakan bentuk mutlak berada di ruas kiri.
Pada bentuk ini ada dua penyelesaian.
Pertama :
x + 5 = 3 , maka x = 3 – 5 = -2
Kedua :
x + 5 = -3, maka x = -3 – 5 = -8
Jadi, himpunan penyelesaiannya adalah {-2, -8}
12. Tentukan himpunan penyelesaian dari persamaan nilai mutlak | 2x – 3 | = 5 adalah. . .
Jawaban :
Pada bentuk ini ada dua penyelesaian.
Pertama :
2x + 3 = 5 , maka 2x = 5 – 3
2x = 2 ↔ x = 1
Kedua :
2x + 3 = -5 , maka 2x = -5 -3
2x = -8 ↔ x = – 4
Jadi, himpunan penyelesaiannya adalah {-4, 1}
13. Tentukan himpunan penyelesaian dari persamaan nilai mutlak | x + 1 | + 2x = 7 adalah. . .
Jawaban :
Penyelesaian persamaan nilai mutlak ini juga dibagi menjadi dua bagian.
Bagian pertama untuk batasan x+1 ≥ 0 atau x ≥ -1
Bagian kedua untuk batasan x+1< 0 atau x < -1
Mari kita selesaikan.
Bagian pertama
untuk x ≥ -1
Persamaan mutlak dapat ditulis:
(x + 1) + 2x = 7
3x = 7 – 1
3x = 6
= 2 (terpenuhi, karena batasan ≥ -1)
Bagian kedua
untuk x < -1
Persamaan mutlak dapat ditulis:
-(x + 1) + 2x = 7
-x – 1 + 2x = 7
x = 7 + 1
= 8 (tidak terpenuhi, karena batasan < -1)
Jadi, Himpunan penyelesaiannya adalah {2}
14. Tentukan himpunan penyelesaian dari persamaan nilai mutlak | 3x + 4 | = x – 8 adalah. . .
Jawaban :
Perhatikan bentuk aljabar di dalam tanda mutlak, yaitu 3x + 4. Penyelesaian persamaan nilai mutlak ini juga dibagi menjadi dua bagian.
Bagian pertama untuk batasan 3x+4>= 0 atau x >= -4/3
Bagian kedua untuk batasan 3x+4< 0 atau x < -4/3 Mari kita selesaikan.
Bagian pertama
untuk x >=-4/3
Persamaan mutlak dapat ditulis:
(3x + 4) = x – 8
3x – x = -8 – 4
2x =-12
x = -6 (tidak terpenuhi, karena batasan >= -4/3)
Bagian kedua
untuk x < -4/3
Persamaan mutlak dapat ditulis:
-(3x + 4) = x – 8
-3x – 4 = x -8
-3x – x = -8 + 4
-4x = -4
x = 1 (tidak terpenuhi, karena batasan < -4/3)
Jadi, Tidak ada Himpunan penyelesaiannya.
15. Tentukan himpunan penyelesaian dari persamaan nilai mutlak |5 – 2/3 x| – 9 = 8 adalah. . .
Jawaban :
Dengan mengisolasi simbol nilai mutlak baru kemudian menerapkan sifat persamaan nilai mutlak, kita mendapatkan :
Sehingga, himpunan selesaian dari persamaan tersebut adalah {–18, 33}.
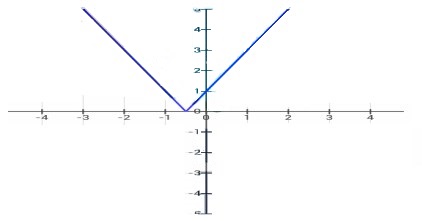
16. Gambarkan grafik untuk fungsi f (x) = | x + 1 | , g (x) = | 2x + 1 | , h (x) = | 4x + 1 | Simpulkan perbedaan bentuk grafik dari 3 fungsi tersebut !
Jawaban :
Pembahasan :
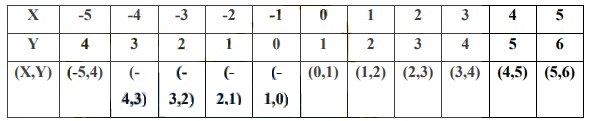
f (x) = | x + 1 |
Langkah 1 Membuat Tabel
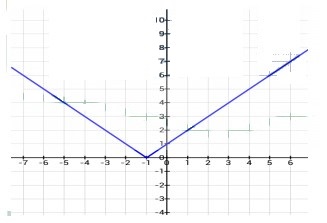
Langkah 2 Membuat Grafik
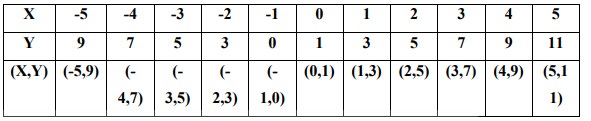
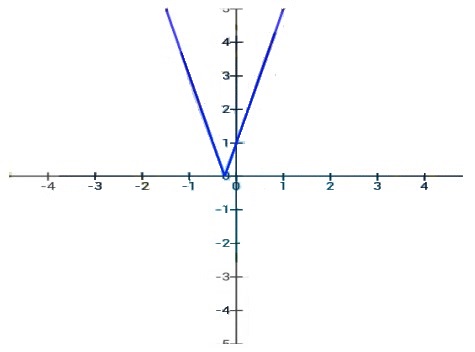
g (x) = | 2x + 1 |
Langkah 1 Membuat Tabel
Langkah 2 Membuat Grafik
h (x) = | 4x + 1 |
Langkah 1 Membuat Tabel
Langkah 2 Membuat Grafik
Kesimpulan dari ketiga perbedaan gambar tersebut adalah Semakin besar pengali x maka akan semakin tampak tajam dan semakin kerucut hamper menyerupai huruf v atau berbentuk segitiga panah semakin kurus
17. Gambarlah dalam grafik Cartesius untuk persamaan linier berikut !
y = | 3x – 2 | + | x – 1 |
Jawaban :
Pembahasan :
y = | 3x – 2 | + | x – 1 |
18. Tentukan |x + 3 | untuk x bilangan real adalah. . .
Jawaban :
Pembahasan :
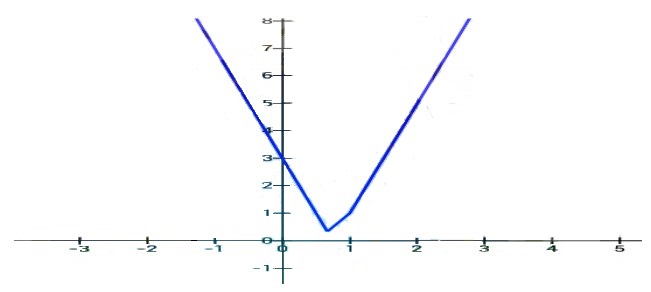
19. Tentukan |-2x + 5 | untuk x bilangan real adalah. . .
Jawaban :
Pembahasan :
20. Tentukan nilai :
a) |-4 | + | 5 | – | -3 |
b) |-9 | + | -2 |
c) Untuk x = -3 , tentukanlah nilai | x2 + 6x + 5 |
Jawaban :
Pembahasan :
21 – 25 Soal Persamaan Nilai Mutlak dan Jawaban
21. Tentukan nilai x yang memenuhi persamaan : | 3 – 2x | = 7
Jawaban :
Pembahasan :
22. Tentukan nilai x yang memenuhi persamaan | 2x – 5 | = 3 adalah. . .
Jawaban :
Pembahasan :
Dengan menggunakan sifat berikut :
maka diperoleh penyelesaian :
23. Tentukan nilai x yang memenuhi persamaan | 2x – 4 | = | x – 1 | adalah. . .
Jawaban :
Pembahasan :
Dengan menggunakan sifat berikut :
maka diperoleh penyelesaian :
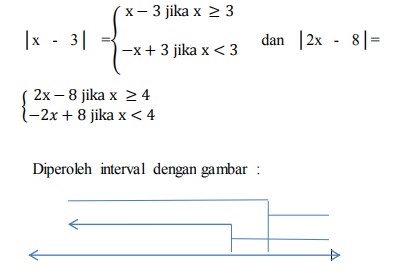
24. Terdapat persamaan | x – 3|+ | 2x – 8 | = 5 .
a) Tentukan nilai x yang memenuhi persamaan dan buatlah kesimpulan dari jawabanmu!
b) Gambarlah garis bilangan untuk melihat intervalnya!
Jawaban :
Pembahasan :
Dik :
Persamaan │x – 3│+ │2x – 8│ = 5
Dit :
nilai x yang memenuhi persamaan.
Penyelesaian :
Mencari batas x dari masing-masing persamaan nilai mutlak
Untuk x – 3 = 0
X = 3
Untuk 2x – 8 = 0
2x = 8
X= 4
│x – 3│+ │2x – 8│ = 5 Karena c = 5 , artinya c ≥ 0 maka berlaku :
Sehingga diperoleh persamaan sebagai berikut :
Untuk x < 3 maka bentuk │x – 3│ + │2x – 8│ menjadi
–x + 3 – 2x + 8 = 5
-3x + 11 = 5
-3x = -6
x = 2
(memenuhi karena x = 2 berada pada domain x < 3 )
Untuk 3 ≤ x < 4 maka bentuk│x – 3│ + │2x – 8│ menjadi :
x – 3 – 2x + 8 = 5
-x + 5 = 5
-x = 0
x = 0
(tidak memenuhi karena x = 0 tidak berada pada domain 3 ≤ x < 4 )
Untuk x ≥ 4 maka bentuk │x – 3│ + │2x – 8│ menjadi :
x – 3 + 2x – 8 = 5
3x – 11 = 5
3x = 16
X = 16/3
(memenuhi karena x = 16/3 berada pada domain x ≥ 4 )
Jadi , nilai x yang memenuhi penyelesaian adalah x = 2 dan x=16/3
25. Tentukan penyelesaian dari persamaan x + 16 = 19, x adalah himpunan bilangan cacah dan tentukan pula akar PLSV serta himpunan penyelesaiannya.
a) Tentukan Penyelesaian dan juga himpunan
b) Tentukan akar PLSV
Jawaban :
Pembahasan :
Dik :
persamaan x + 16 =19
Dit :
nilai x dan himpuan
Penyelesaian : Untuk x = 1 , maka 1 + 16 = 17 ( salah )
Untuk x = 2 , maka 2 + 16 = 18 ( salah )
Untuk x = 3 , maka 3 + 16 = 19 ( benar )
Untuk x = 4 , maka 4 + 16 = 20 ( salah )
X = 3 merupakan penyelesaian x + 16 = 19
X = 3 merupakan akar PLSV x + 16 = 19
Hp = {3}
Jadi , akar dari PLSV x + 16 = 19 yang merupakan himpunan penyelesaian adalah x = 3
Sudah selesai membaca dan berlatih Soal Persamaan Nilai Mutlak ini ? Ayo lihat dulu Soal Matematika lainnya



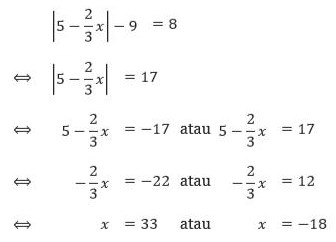

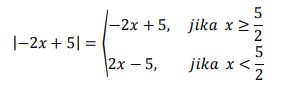
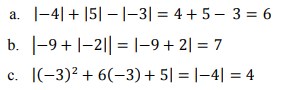

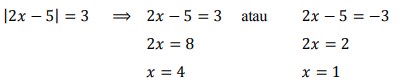
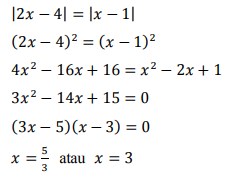



a. Mungkinkah persamaan di atas tidak memiliki solusi. Jika mungkin,
tentukan nilai a.
b. Mungkinkah persamaan di atas memiliki satu solusi. Jika mungkin,
tentukan nilai a
c. Mungkinkah persamaan diatas memiliki dua solusi. Jika mungkin,
tentukan nilai a.
d. Mungkinkah persamaan di atas memiliki 3 solusi. Jika mungkin, tentukan Nilai a
Klo in gimana?
Oooo seperti itu
12 itu yang bener mana pake + apa –
Saya mulai paham sedikit-sesikit tentang
Persamaan nilai mutlak.
saya mulai paham sedikit tentang persamaan nilai mutlak 6