Contoh Soal Deret Geometri Tak Hingga Pilihan Ganda dan Jawabannya – Deret geometri tak hingga merupakan suatu deret geometri dapat menjumlahkan suku-sukunya sampai menuju tak hingga. Apabila deret geometri menuju tak hingga dimana n → ∞ .

Secara umum Deret geometri merupakan penjumlahan suku-suku dari suatu barisan geometri. Penjumlahan dari suku suku petama sampai suku ke-n barisan geometri.
Deret aritmatika merupakan penjumlahan suku-suku dari suatu barisan aritmatika. Penjumlahan dari suku-suku petama sampai suku ke-n.
Misalkan selembar kertas berbentuk segiempat dibagi menjadi 2 dan salah satu bagiannya dibagi lagi menjadi 2 bagian. Bagian ini dibagi lagi menjadi 2 dan begitu seterusnya seperti gambar berikut ini:
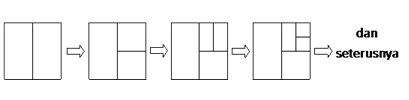
Secara teoritis pembagian ini dapat dilakukan berulang kali sampai tak hingga kali. Pada pembagian pertama diperoleh setengah bagian, yang kedua seperempat bagian, yang ketiga seperdelapan bagian dan seterusnya sampai tak hingga kali.
Tampak jelas bahwa jumlah dari seluruh hasil pembagian sampai tak hingga kali tetap = kertas semula (1 bagian). Hasil ini dapat dituliskan:
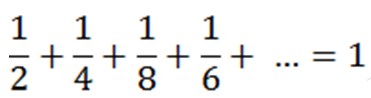
1 – 11 Soal Deret Geometri Tak Hingga dan Jawaban
1. Jumlah bilangan diantara 5 dan 100 yang habis dibagi 7 tetapi tidak habis dibagi 4 adalah…
A. 168
B. 567
C. 651
D. 667
E. 735
Jawaban : B
Pembahasan :
Jumlah bilangan diantara 5 dan 100 yang habis dibagi 7 tetapi tidak habis dibagi 4 adalah :
hasil (1) – hasil (2) = 735 – 168 = 567
Jawabannya adalah B
2. Dari suatu barisan geometri diketahui suku ke 2 adalah 34 dan suku ke 5 adalah 36. Suku ke 6 barisan tersebut adalah….
A. 108
B.120
C.128
D. 240
E. 256
Jawaban : A
Pembahasan :
Jawabannya adalah A
3. Dari suatu deret geometri yang rasionya 2 diketahui jumlah 10 buah suku pertama sama dengan 3069. Hasil kali suku ke 4 dan ke 6 dari deret tersebut=….
A. 3069
B. 2304
C. 4236
D. 4476
E. 5675
Jawaban : B
Pembahasan :
4. Sebuah mobil dibeli dengan harga Rp.80.000.000,- Setiap tahun nilai jualnya menjadi ¾ dari harga sebelumnya. Berapa nilai jual setelah 3 tahun . . .
A. Rp. 20.000.000,-
B. Rp. 25.312.000,-
C. Rp. 33.750.000,-
D. Rp. 35.000.000,-
E. Rp. 45.000.000,-
Jawaban : E
Pembahasan :
Diketahui harga awal = a = 80.000.000
r = ¾
Nilai jual setelah 3 tahun = suku ke 3 = U3
Jawabannya adalah E
5. Jumlah n suku pertama suatu deret geometri ditentukan oleh rumus Sn = 2n+2 – 4. Rasio dari deret tersebut adalah…
A. 8
B. 4
C. 2
D. ½
E. ¼
Jawaban : C
Pembahasan :
Jawabannya adalah C
Baca Juga : Soal Kombinatorika (Permutasi dan Kombinasi)
6. Jumlah deret geometri tak hingga dari :
A. 48
B. 24
C. 19.2
D. 18
E. 16.9
Jawaban : B
Pembahasan :
Jawabannya adalah B
8. Agar deret bilangan :
jumlahnya mempunyai limit, nilai x harus memenuhi…
A. x > 0
B. x < 1
C. 0<x< 1 atau x >1
D. x >2
E. 0<x< 1 atau x >2
Jawaban : D
Pembahasan :
Jawabannya adalah D
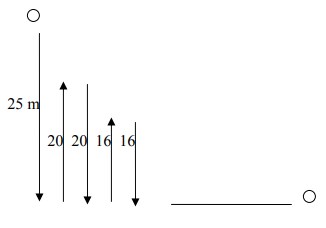
9. Sebuah bola pingpong dijatuhkan dari ketinggian 25m dan memantul kembali dengan ketinggian 4/5 kali tinggi sebelumnya. Pemantulan ini berlangsung terus menerus hingga boleh berhenti. Jumlah seluruh lintasan bola adalah..
A. 100m
B. 125m
C. 200m
D. 225m
E. 250m
Jawaban : D
Pembahasan :
Menjawab soal ini dengan membayangkan pergerakan bola pingpong tersebut yang digambarkan dengan sketsa gambarnya sebagai berikut:
terlihat pada gambar 20m dan 16m dan selanjutnya nya terdiri dari dua kejadian: pantulan 4/5 dari tinggi sebelumnya naik ke atas dan dengan jarak yang sama turunnya.
Sehingga terjadi 2 kejadian deret yaitu naik dan turun
a = 20 (bukan 25, deret terjadi awalnya pada 20)
Jawabannya adalah D
10. Jumlah suatu deret geometri tak hingga adalah 30 dengan rasio 2/3. Suku pertama deret tersebut adalah…
A. 2
B. 4
C. 6
D. 8
E. 10
Jawaban : E
Pembahasan :
11. Jika rasio suatu deret geometri tak hingga adalah 2/3 dan suku pertamanya adalah 6 maka jumlah deret tersebut adalah…
A. 20
B. 18
C. 16
D. 14
E. 12
Jawaban : B
Pembahasan :
12. Suku ke-n suatu deret geometri adalah 4-n. Maka jumlah tak hingga deret tersebut sama dengan
A. 3
B. 2
C. 1
D. ½
E. 1/3
Jawaban : E
Pembahasan :
Un = 4-n dari persamaan ini sobat dapat menentukan :
a = U1 = 4-1, U2 = 4-2
r = U2/U1 = 4-2/4-1 = 4-1 = 1/4
Sn→ ∞ = a/[1-r] = 1/4 : [1-1/4] = 1/4 : 3/4 = 1/4 x 4/3 = 1/3
13. Suku-suku suatu barisan geometri takhingga adalah positif, jumlah suku U1+U2 = 45 dan U3 + U4 = 20, maka berapa jumlah suku-suku dalam barisan tersebut adalah. . .
A. 65
B. 81
C. 90
D. 135
E. 150
Jawaban : B
Pembahasan :
diketahui :
(Pertama) U1 + U2 = 45
→ a + ar = 45
→ a (1+r) = 45 ………….. (1)
(Kedua) U3 + U4 = 20
→ ar² + ar³ = 20
→ r² a(1+r) = 20 ……..(2)
kita substitusi persamaan (1) ke persamaan (2)
r² (45) = 20
r² = 20/45 = 4/9
r = 2/3 atau –2/3
karena suku-suku deret geometrinya diketahui positif maka r = 2/3
kita bisa menentukan nilai a
a (1+ 2/3) = 45
a x 5/35 = 45
a = 45 x 3/5
a = 27
dengan demikian jumlah suku-suku barisan geometri hingga tersebut adalah
S = a/1-r = 27/ (1-2/3) = 27 : 1/3 = 27 x 3 = 81
14. Jika jumlah takhingga deret a + a0 + a-1 + a-2 + a-3 + … adalah 4a, maka nilai a adalah
A. 4/3
B. 2
C. 3/2
D. 3
E. 4
Jawaban : A
Pembahasan :
deret dalam soal di atas adalah deret geometri dengan suku pertama (a) = a
r = 1/a dan S = 4a kita masukkan ke rumus
S = a/[1-r] 4a = a/[1-1/a] 4a = a²/[a-1] 4a [a-1] = a²
4a² – 4a = a² (masing-masing ruas di kali 1/a)
4a – 4 = a
3a = 4
a = 4/3
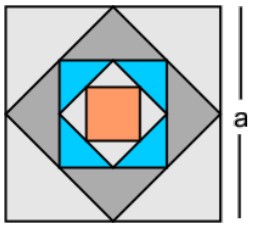
15. Hitunglah gambar bujur sangkar di bawah. Jika gambar tersebut diteruskan maka total jumlah luasnya adalah . . .
a. 2a²
b. 3a²
c. 4a²
d. 5a²
e. tak hingga
Jawaban : A
Pembahasan :
Luas I = a x a = a²
Luas II = ½ a²
Luas III = ¼ a²
dan seterusnya, dari deret geometri di atas terlihat nilai suku awal = a² dan rasio = ½
Sn→∞ = a/[1-r] = a²/0,5 = 2a²
Simak Juga : Soal Fungsi Komposisi dan Invers
16. hitunglah sebuah benda bergerak lurus dengan kecepatan tetap 4 km/jam selama 1 jam pertama. Pada jam kedua kecepatan dikurangi menjadi setengahnya, demikian seterusnya, setiap jam kecepatan menjadi setengah dari kecepatan jam sebelumnya. Berapa km jarak terjauh dari benda tersebut adalah. . .
A. tak tentu
B. tak hingga
C. 8 km
D. 10 km
E. 13 km
Jawaban : C
Pembahasan :
jarak yang ditempuh oleh sobat membentuk deret geometri 4 + 2 + 1 + ½ + ¼ + ….
a = 4
b = ½
n → ∞ = a/[1-r] = 4/[1-½] = 4/0,5 = 8 km
17. Sebuah bola jatuh dari ketinggian 10 m dan memantul kembali dengan ketinggian ¾ kali tinggi sebelumnya, begitu seterusnya hingga bola berhenti. Jumlah seluruh lintasan bola adalah …
A. 65m
B. 70m
C. 75m
D. 77m
E. 80m
Jawaban : B
Pembahasan :
Karena bola memantul terus-terusan sampai berhenti, berarti ini termasuk deret geometri tak hingga. Untuk mencari panjang lintasan bola yang memantul ini, rumus yang digunakan adalah
Panjang lintasan = ketinggian bola jatuh + 2 (kali deret tak hingga)
Dalam deret tak hingga ini, yang menjadi suku pertama ya adalah pantulan pertama (bukan ketinggian bola jatuh pada awal)Pantulan pertama = 10 x ¾ = 30/4 m (suku pertama) = 10 x 3 :30
P.Lintasan = 10 + 2(30) = 70m
18. Sebuah bola pingpong dijatuhkan dari ketinggian 25 m dan memantul kembali dengan ketinggian 4/5 kali tinggi semula. Pemantulan ini berlangsung terus menerus hingga bola berhenti. Jumlah seluruh lintasan bola adalah … m.
A. 100
B. 125
C. 200
D. 225
E. 250
Jawaban : D
Pembahasan :
Karena bola memantul terus-terusan sampai berhenti, berarti ini termasuk deret geometri tak hingga. Untuk mencari panjang lintasan bola yang memantul ini, rumus yang digunakan adalah
Panjang lintasan = ketinggian bola jatuh + 2(kali deret tak hingga)
Dalam deret tak hingga ini, yang menjadi suku pertama nya adalah pantulan pertama (bukan ketinggian bola jatuh pada awal).
Pantulan pertama = 25 x 4/5 = 20m (suku pertama)
25 x 4=100
P.Lintasan = 25 + 2(100) = 225m
Sudah selesai membaca dan berlatih soal ini ? Ayo lihat dulu Soal Matematika lainnya


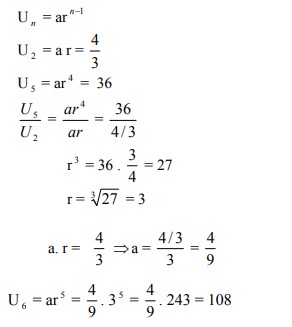
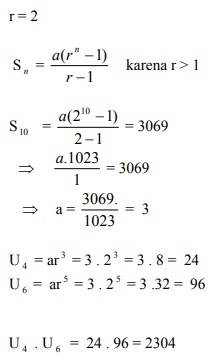
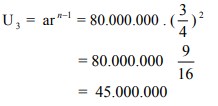

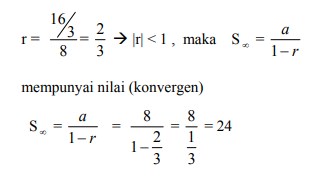


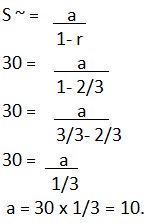
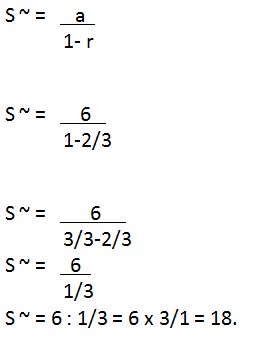



Makasih pak GURU, kami telah menemukan subuah web SOAL KIMIA COM yang memuat berbagai pelajaran dalam bentuk “soal dan pembahasan”. Tentu hal ini sangat membantu para siswa yang saat mereka harus belajar mandiri akibat Covid 19. Kiranya bapak ibu guru di web ini tetap mengembangkan karya-karya ini demi para siswa anak Indonesia. Salam.