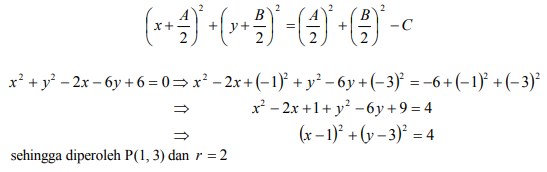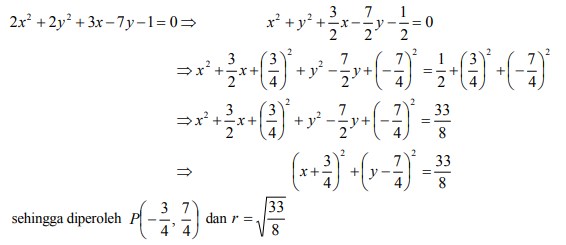Contoh Soal Unsur-unsur Keliling, dan Luas Lingkaran dan Jawaban – Lingkaran merupakan sekumpulan titik-titik yang membentuk lengkungan yang memiliki panjang sama terhadap titik pusat lingkaran. Lengkungan-lengkungan pada lingkaran saling bertemu mengelilingi titik pusat dan membentuk daerah di dalamnya.

Sebuah lingkaran memiliki unsur-unsur tertentu yang berbeda dengan bangun datar lain.
Jari-jari (r) Jari-jari lingkaran dilambangkan dengan huruf r, yang akan berguna saat menghitung luas dan keliling lingkaran.
Titik pusat adalah titik yang berada tepat pada bagian tengah bangun lingkaran.
Busur lingkaran merupakan suatu garis lurus yang dibuat di dalam daerah lingkaran, baik itu garis terbuka ataupun garis tertutup yang menghimpit lengkungan lingkaran.
Tali busur merupakan garis lurus yang berada dalam daerah lingkaran yang memisahkan lingkaran menjadi dua titik berbeda.
Diameter (d) merupakan garis yang tepat membagi lingkaran menjadi dua bagian yang sama.
Tembereng merupakan luas suatu daerah di dalam bangun lingkaran yang kedua sisinya merupakan busur dan tali busur.
Apotema merupakan sebuah garis tegak lurus dengan tali busur, yang menghubungkan bagian titik pusat dan tali busur sabuah lingkaran.
Juring adalah daerah di dalam lingkaran yang sisinya dibatasi dua jari-jari dan busur lingkaran. Seperti temberena, juring ada dua macam, yakni juring kecil dan juring besar.
1 – 10 Contoh Soal Unsur, Keliling, dan Luas Lingkaran dan Jawaban
1. Tentukan persamaan lingkaran yang berpusat di P(0,0) dengan jari-jari r = 5.
Jawaban :
Persamaan lingkaran dengan pusat P(0,0) dan jari- jari r adalah x 2 + y 2 = r 2 , (Bentuk Baku)
maka persamaan lingkaran yang berpusat di P(0,0) dengan jari-jari r = 5 adalah:
x2 + y2 = r2
⇒ x2 + y2 = 52
⇒ x2 + y2 = 25
2. Tentukan persamaan lingkaran yang berpusat di P(3,5) dengan jari-jari r = 9.
Jawaban :
Persamaan lingkaran dengan pusat P(a, b) dan jari- jari r adalah
(x – a)2 + (y – b)2 = r 2 , (Bentuk Baku)
maka persamaan lingkaran yang berpusat di P(3,5) dengan jari-jari r = 9 adalah:
3. Tentukan pusat dan jari-jari lingkaran x2 + y2 = 10
Jawaban :
x 2 + y2 = 10 ⇒ x 2 + y 2 = √(10)2 , sehingga P(0,0) dan r = 10
4. Tentukan pusat dan jari-jari lingkaran (x + 5)2 + (y – 4)2 = 49
Jawaban :
(x + 5)2 + (y – 4)2 = 49 ⇒ (x – (- 5))2 + (y – 4)2 = 72 , sehingga P (– 5, 4) dan r = 7
5. Tentukan pusat dan jari-jari lingkaran x2 + y2 – 2x – 6 y + 6 = 0
Jawaban :
Persamaan lingkaran dalam bentuk umum x2 + y2 + Ax + By + C = 0 dapat diubah dalam bentuk baku (dengan melengkapkan bentuk kuadrat) sebagai berikut:
Simak Juga : Soal Turunan Fungsi Aljabar
6. Tentukan pusat dan jari-jari lingkaran 2x2 + 2y2 + 3x – 7y – 1 = 0
Jawaban :
7. Diketahui lingkaran dengan persamaan x2 + y2 + ax + by + 19 = 0 melalui titik A(- 2, 9) dan B(4, 3), maka nilai a + b = ….
Jawaban :
Titik A(- 2, 9) dan B(4, 3) dilalui L º x 2 + y 2 + ax + by + 19 = 0 , maka
A(- 2, 9): (-2)2 +92 +a(-2)+b.9 +19= 0 Þ4 +81-2a +9b +19= 0 ⇒ -2a+9b = -104 …(1)
B(4, 3): 42 +32 +a.4+b.3+19= 0 Þ16+9+ 4a+3b +19=0 ⇒ 4a+3b = -44 …(2)
8. Tentukan pusat dan jari-jari lingkaran Lº x2 + y2 – 6x + py + 9 = 0 yang melalui titik T (5, 1).
Jawaban :
9. Tentukan persamaan lingkaran yang melalui titik A(–5, 6) dan B(3, 2) dimana AB adalah diameter lingkaran tersebut.
Jawaban :
Persamaan lingkaran melalui titik A(x1 , y1 ) dan B(x2 , y2 ), dimana AB adalah diameter lingkaran adalah: (x – x1 )(x – x2 ) + (y – y1 )(y – y2 ) = 0
Jadi persamaan lingkaran melalui titik A(–5, 6) dan B(3, 2) dimana AB diameter lingkaran adalah:
(x + 5)(x – 3) + (y – 6)(y – 2) = 0
⇒ x2 + 2x -15 + y 2 – 8 y + 12 = 0
⇒ x2 + y 2 + 2x – 8y – 3 = 0
10. Tentukan persamaan lingkaran yang melalui titik-titik A(2, – 4), B(5, -1) dan C(2, 2).
Jawaban :
11 – 20 Contoh Soal Unsur, Keliling, dan Luas Lingkaran Pilihan Ganda dan Jawaban
11. Tentukan persamaan lingkaran dengan pusat P(4, 2) dan menyinggung garis g ≡ 2x + y = 4 .
Jawaban :
12. Tentukan persamaan lingkaran dengan pusat P(4, 2) melalui titik T(3, -1).
Jawaban :
13. Tentukan persamaan lingkaran dengan pusat P(-5, 6) dan garis tangen sumbu X.
Jawaban :
14. Tentukan persamaan lingkaran dengan pusat P(3, -4) dan garis tangen sumbu Y.
Jawaban :
15. Tentukan persamaan lingkaran dengan pusat P(-2, 5) dan garis tangen x = 7
Jawaban :
Lihat Juga : Soal Bangun Ruang
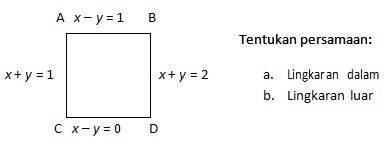
16. Sisi-sisi persegi mempunyai persamaan sebagai berikut:
Jawaban :
AB : x – y = 1 ………………..(1)
CD : x – y = 0 ………………(2)
AC : x + y = 1 ………………(3)
BD : x + y = 2 ……………..(4)
a). Lingkaran dalam
b). Lingkaran luar
17. Tentukan persamaan lingkaran yang melalui titik T (-3, 4) dan sepusat dengan lingkaran x2 + y2 + 8x – 4y – 1 = 0 .
Jawaban :
18. Tentukan persamaan lingkaran yang menyinggung sumbu X dan sumbu Y, jika pusatnya terletak pada garis 5x – 4 y = 3 .
Jawaban :
19. Selidikilah apakah persamaan-persamaan berikut merupakan persamaan lingkaran atau bukan, jika bukan sebutkan alasannya.
a). (x – 1)2 + (y – 7)2 – 36 = 0
b). x 2 + y2 – 4x – 8 y + 25 = 0
Jawaban :
20. Tentukan batas nilai p agar persamaan x 2 + y 2 + px + 2 y + 26 = 0 menunjukkan sebuah lingkaran
Jawaban :
Nilai p yang memenuhi adalah p < – 10 atau p > 10
Sehingga x2 + y2 + px + 2y + 26 = 0 merupakan persamaan lingkaran jika p < – 10 atau p > 10.
21. Diketahui lingkaran L1 = x2 + y2 + 6x – 10y +18 = 0 . Akan dibuat lingkaran baru L2 dengan titik pusat adalah titik pusat lingkaran L1 dicerminkan terhadap sumbu X dan jari-jarinya diperbesar menjadi 2 kali jari- jari L1 . Tentukan persamaan lingkaran tersebut!
Jawaban :
L1 ≡ x 2 + y 2 + 6x -10y +18 = 0 mempunyai pusat
Sudah selesai membaca dan berlatih Soal ini ? Ayo lihat dulu Daftar Soal Matematika lainnya