Contoh Soal Suku Banyak (Polinomial) Pilihan Ganda dan Pembahasannya – Suku banyak (polinomial) adalah sebuah ungkapan aljabar yang variabel (peubahnya) berpangkat Bilangan bulat non negatif.
Bentuk umum :
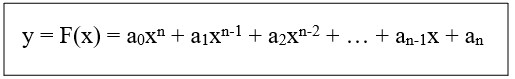
Dengan n Є bilangan bulat :
an ≠ 0
Pengertian-pengertian:
a0, a1, a2 ,…, an-1 , an
Disebut koefisien masing-masing bilangan real (walaupun boleh juga bilangan kompleks)
Derajat Suku Banyak adalah pangkat tertinggi dari pangkat-pangkat pada tiap-tiap suku, disebut n.Untuk suku banyak nol dikatakan tidak memiliki derajat.
Suku : a0xn , a1xn-1 , a2xn-2 , … , an-1x , an Masing-masing merupakan suku dari suku banyak.
Secara umum pengertian Suku banyak adalah pernyataan matematika yang berhubungan dengan jumlahan perkalian pangkat dalam satu atau lebih variabel dengan koefisien.
Pembagian Polinomial
Metode Pembagian Biasa
Metode Horner
Metode Koefisien Tak Tentu

1 – 10 Soal Suku Banyak dan Jawaban
1. Tulislah menurut urutan pangkat turun dari variabel suku banyak berikut ini dan tentukan derajatnya.
a) 6x2 +2x + 7x3– 2
b) (1 – x)(x – 2)
c) y(y + 1)(y2 + y + 5)
Jawaban :
2. Tentukan koefisien dari:
a) x dalam (2x -1)(4 – 3x)
b) x2 dalam (x – 1)(2x – 1)(x2 + x + 1)
Jawaban :
3. Manakah setiap bentuk berikut yang merupakan suku banyak? Jika bukan, apakah alasannya?
a) (x – 2)(x + 3)
b) x 2 – 3x + 2/x
c) 2√x + 3x – 4
Jawaban :
4. Tentukan suku banyak berderajat 5 yang koefisien x dari variabel berpangkat tertinggi ke terendah adalah 3, 2, -1, 0, 0, 3…
Jawaban :
Suku banyak tersebut adalah
3x 5 + 2x 4 – x 3 + 0x 2 + 0x +3 = 3x 5 + 2x 4 – x 3 + 3
5. Tentukan nilai p dan q dari kesamaan suku banyak px 2 + qx – 3 = 2 x – 3 – 5x2 adalah . . .
Jawaban :
Simak Juga : Soal Program Linear
6. Tentukan nilai A, B, dan C jika diketahui:
11x 2 + 4x + 12 = A(x 2 + 4)+ (Bx + C )(2 x + 1) adalah. . .
Jawaban :
11x2 + 4x + 12 = A(x 2 + 4)+ (Bx + C)(2x +1)
Ax 2 + 4A + 2Bx 2 + 2Cx + Bx + C
(A + 2B)x2 + (B + 2C )x + (4A + C)
Diperoleh:
A+ 2B =11 ⇒ A=11- 2B ….(1)
B+2C=4 ….(2)
4A+C =12….(3)
Subtitusi (1) ke (3):
4(11- 2B)+ C = 12 ⇒ 44 – 8B + C =12 ⇒ -8B + C = -32
7. Jika P(x ) = x 3 – 3x 2 + x + 1 , hitunglah nilai P(2) adalah …
Jawaban :
Cara 1: Subtitusi
P( x) = x 3 – 3x 2 + x +1⇒ P(2) = 23 – 3.22 + 2 +1
= 8 -12+ 3
= -1
Cara 2: Horner
8. Tentukan nilai x yang menjadikan suku banyak berikut bernilai nol. f (x ) = x 2 – 7x + 6
Jawaban :
f (x ) = 0
x2 – 7x + 6 = 0
(x -1)(x – 6) = 0
(x -1) = 0 atau (x – 6) = 0
x = 1 atau x = 6
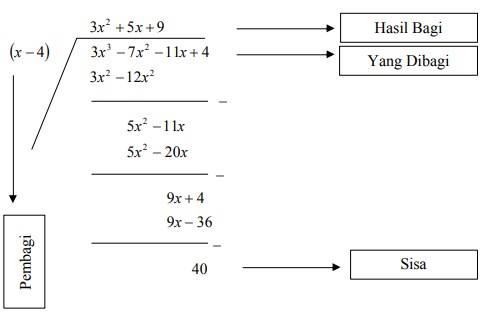
9. Tentukan hasil bagi dan sisa pembagian suku banyak 3x3 – 7x2 -11x + 4 oleh (x – 4)
Jawaban :
Cara 1: Pembagian Bersusun
Jadi, diperoleh hasil bagi H (x) = 3x2 + 5x + 9 dan sisa = 40.
Cara 2: Horner
Pembagi (x – 4) ⇒ a = 4
10. Tentukan hasil bagi dan sisa pembagian suku banyak 6x 3 -16x 2 + 16 x -16 oleh (2x – 4) adalah. . .
Jawaban :
Horner
11 – 20 Contoh Soal Suku Banyak dan Jawaban
11. Tentukan hasil bagi dan sisa pembagian suku banyak F (x) = x3 + 2x2 + 4 x + 6 oleh P(x) = x2 – 3x + 2 adalah. . .
Jawaban :
Jadi, diperoleh hasil bagi H (x) = x + 5 dan sisa
12. Tentukan sisa F (x) = 2x 2 – 13 x + 11 dibagi oleh x – 3 adalah. . .
Jawaban :
Teorema Sisa:
Jika suku banyak F(x) dibagi oleh (x – a), maka sisanya adalah F (a) .
Demikian juga:
Jika suku banyak F(x) dibagi oleh (ax + b), maka sisanya adalah F(- b/a ) .
Maka sisa F (x) = 2x 2 – 13 x + 11 dibagi oleh x – 3 adalah:
Sisa = F (3) = 2.32 – 13 .3 + 11 = 18 – 39 + 11 = -10
13. Tentukan sisa F (x) = 2x3 + 5x2 – 7 x + 3 dibagi oleh x2 – 4
Jawaban :
Pembagi x 2 – 4 bisa difaktorkan, yaitu P( x) = P1(x).P2(x) = (x – 2)(x + 2)
Catatan: Jika pembagi berderajat dua dan bisa difaktorkan, maka bisa digunakan cara Horner. Jika tidak bisa difaktorkan maka pakai cara pembagian bersusun.
14. Tunjukkan bahwa (x – 2) adalah faktor dari F (x) = x3 – 2x2 – x + 2
Jawaban :
Teorema faktor:
Suku banyak F(x) mempunyai faktor (x – a), jika dan hanya jika F (a) = 0 .
F(2)=23 – 2.22 – 2 + 2 = 8 – 8 – 2 + 2 = 0
Jadi, benar bahwa (x – 2) adalah faktor dari F (x) = x3 – 2x2 – x + 2
15. Tentukan faktor dari suku banyak berikut: x 3 + 2 x 2 – x – 2
Jawaban :
Suku banyak tersebut mempunyai konstanta – 2. Faktor dari – 2 adalah ± 1, ± 2 Subtitusi ke dalam suku banyak:
x =1 ⇒ 13 +2.12 -1-2=0
x = -1 ⇒ (-1)3 + 2(-1)2 – (-1) – 2 = 0
x = 2 ⇒ 23 + 2.2 2 – 2 – 2 =12
x = -2 ⇒ (-2)3 + 2(-2) 2 – (-2) – 2 = 0
Maka faktor-faktornya adalah (x -1) , (x +1), dan (x + 2) .
Baca Juga : Soal Ujian Matematika Kelas 10 SMA Semester 1 K.13
16. Tentukan faktor dari suku banyak berikut: 2 x4 – 9 x3 + 5x2 – 3x – 4 adalah. . .
Jawaban :
Suku banyak tersebut mempunyai konstanta – 4. Faktor dari – 4 adalah 1,±2,±4
Karena koefisien variabel pangkat tertinggi = 2, maka faktor lain yang mungkin adalah (faktor- faktor di atas dibagi 2) ±½
17. Tentukan p sehingga 2x4 + 9x3 + 5x2 + 3x + p habis di bagi oleh (x -1) adalah. . .
Jawaban :
F(x) habis dibagi (x – 1) artinya (x – 1) adalah faktor dari F(x), sehingga F(1) = 0
2.14 + 9.13 + 5.12 + 3.1 + p = 0 ⇒ 2 + 9 + 5 + 3 + p = 0
⇒ 19 + p = 0
⇒ p = -19
Jadi, nilai p adalah – 19
18. Hitunglah a dan b jika x4 + 2x3 – 7x2 + ax + b habis dibagi x2 + 2 x – 3 adalah. . .
Jawaban :
19. Tentukan akar-akar persamaan suku banyak x3 – 6x2 + 11x – 6 = 0 adalah. . .
Jawaban Soal suku banyak :
cara 1 :
Perhatikan suku yang memuat konstanta saja, yaitu – 6, maka akar-akar yang mungkin adalah: ± 1, ± 2, ± 3, ± 6
x =1 ⇒ 13 – 6.12 +11.1- 6 = 1 -6 + 11- 6 = 0 (1 akar suku banyak tersebut)
x = -1 ⇒ (-1)3 – 6.(-1)2 +11.(-1) – 6 = -1 -6 -11 -6 = -24 (-1 bukan akar suku banyak tersebut)
x = 2 ⇒ 23-6.22 +11.2-6=8-24+22- 6= 0 (2 akar suku banyak tersebut)
x = -2 ⇒ (-2)3 – 6.(-2)2 +11.(-2)- 6 = -8 -24 -22 -6 = -60 (-2 bukan akar suku banyak tersebut)
x = 3 ⇒ 33 – 6.32 +11.3- 6= 27- 54+ 33- 6= 0 (3 adalah akar suku banyak tersebut)
x = -3 (tidak perlu dilanjutkan, karena kita sudah mendapatkan 3 akar dari suku banyak berderajat 3, jadi -3 bukan akar suku banyak tersebut)
Jadi, akar-akar suku banyak tersebut adalah 1, 2, dan 3.
Cara 2 :
Diperoleh sisa pembagian = 0, artinya (x – 1) adalah faktor dan 1 adalah akar suku banyak.
diperoleh juga hasil bagi: x 2 – 5x + 6 = (x – 2)(x – 3), artinya 2 dan 3 juga merupakan akar-akar suku banyak tersebut,
Jadi, akar-akar suku banyak tersebut adalah 1, 2, dan 3
20. Tentukan akar-akar persamaan suku banyak 2x3 + 3x2 – 3x – 2 =
Jawaban :
Sudah selesai membaca dan berlatih Soal suku banyak ini ? Ayo lihat dulu Daftar Soal Matematika lainnya

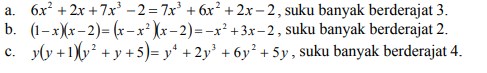
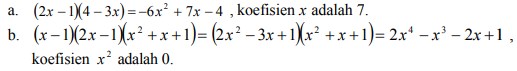

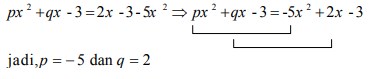





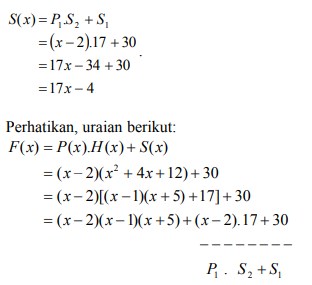








i love your site. it really helps me. thanks.
my pleasure thank you
kaka tolong lihat pembahasan nomor 2a milik kakak.bukannya seharusnya jawabannya 11
kaka tolong lihat pembahasan nomor 2a milik kakak.bukannya seharusnya jawabannya 11
(2x-1)(4-3x)
8x-6x^2-4+3x
-6×2+11x-4
Thank you pembahasan nya 🙂