Contoh Soal Dimensi Tiga (Konsep Jarak: Titik, Garis, dan Bidang) dan Jawaban – Dimensi Tiga adalah ilmu yang dipelajari mencakup tentang konsep titik, garis, dan bidang pada bangun ruang termasuk mengenai jarak dan sudut.

Salah satu topik dalam geometri yang dipelajari oleh siswa di jenjang Sekolah Menengah Atas (SMA) adalah mengenai dimensi tiga.
Materi dimensi tiga yang diajarkan tersebut meliputi konsep kedudukan titik, garis, dan bidang dalam ruang dimensi tiga;
jarak dari titik ke garis dan jarak dari titik ke bidang dalam ruang dimensi tiga;
serta besar sudut antara garis dan bidang dan antara dua bidang dalam ruang dimensi tiga
1 – 10 Contoh Soal Dimensi Tiga dan Jawaban
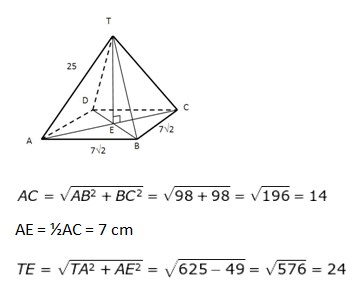
1. Pada limas beraturan T.ABCD, panjang rusuk tegaknya 25 cm dan panjang rusuk alasnya 7√2 cm. Jarak titik T ke bidang ABCD sama dengan …
Jawaban :
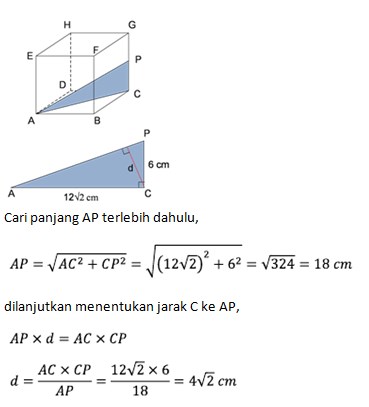
2. Pada kubus ABCD.EFGH dengan panjang rusuk 12 cm, titik P adalah tepat ditengah CG, tentukan jarak titik C ke garis AP!
Jawaban :
Posisi titik C dan garis AP pada kubus sebagai berikut:
3. Panjang rusuk kubus ABCD . EFGH adalah 6 cm. Jika S adalah titik potong EG dan FH, maka jarak DH ke AS adalah …
Jawaban :
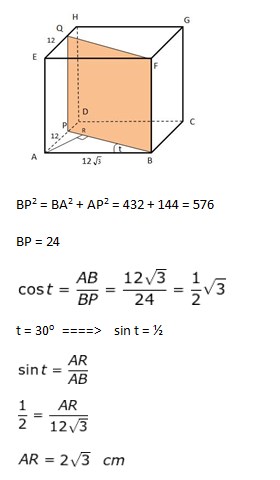
4. Pada kubus ABCDEFGH, titik P pada AD dan titik Q pada EH sehingga AP=EQ = 12 cm. Jika panjang rusuk 12√3 cm maka jarak A ke BPQF sama dengan …
Jawaban :
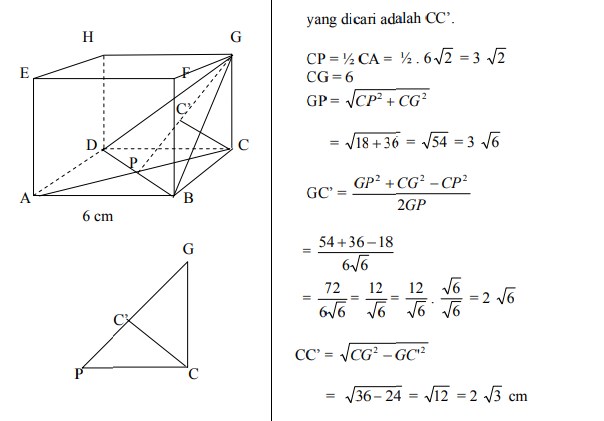
5. Kubus ABCD.EFGH dengan panjang sisi 12 cm. Titik P adalah perpotongan diagonal bidang ABCD. Tentukan jarak titik P ke titik G
Jawaban :
Gambar sebagai berikut
Baca Juga : Soal Persamaan Trigonometri
6. Perhatikan gambar kubus ABCD.EFGH. Jarak titik C dan bidang AFH= ….
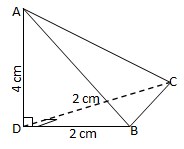
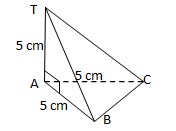
7. Bidang empat ABCD, pada gambar dengan AD tegak lurus alas. Sudut antara bidang BCD dan BCA adalah α, maka tan α = ….
Jawaban :
8. Perhatikan gambar di bawah :
AT, AB dan AC saling tegak lurus di A. Jarak titik A ke bidang TBC adalah ….
Jawaban :
9. Pada kubus ABCD. EFGH, α adalah sudut antara bidang ADHE dan ACH. Nilai cos α = …
Jawaban :
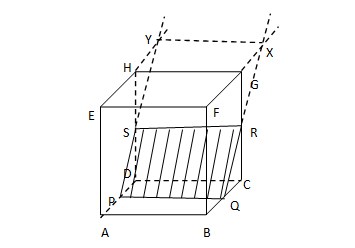
10. Diketahui kubus ABCD. EFGH, titik P,Q,R di pertengahan rusuk AD, BC, dan CG. Irisan bidang yang melalui P, Q dan R dengan kubus berbentuk ….
Jawaban :
Pada kubus ABCD.EFGH, titik P, Q, dan R terletak di pertengahan rusuk AD, BC, dan CG.
Langkah- langkah melukisnya adalah:
Hubungkan titik P dan Q, karena keduanya terletak pada bidang ABCD. PQ adalah sumbu afinitas.
Hubungkan titik Q dan R, karena keduanya terletak pada bidang BCGF.
Perpanjang garis QR dan FG sehingga berpotongan di titik X.
Perpanjang garis EH.
Dari titik X buatlah garis yang sejajar HG sehingga memotong perpanjangan garis EH di titik Y.
Hubungkan titik P dan Y sehingga memotong sisi DCGH di titik S.
Diperolehlah persegi panjang PQRS.
Jadi, irisan bidangnya berbentuk persegi panjang.
11 – 20 Soal Dimensi Tiga dan Jawaban
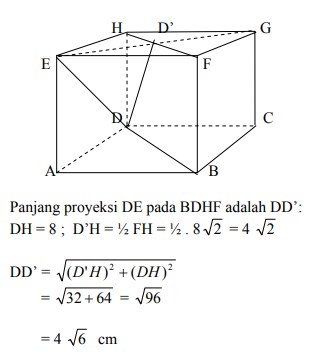
11. Diketahui kubus ABCD.EFGH dengan rusuk 8 cm. Panjang proyeksi DE pada BDHF adalah . . .
A. 2 √2 cm
B. 2 √6 cm
C. 4 √2 cm
D. 4 √6 cm
E. . 8 √2 cm
Jawaban :
Pembahasan :
Jawabannya adalah D
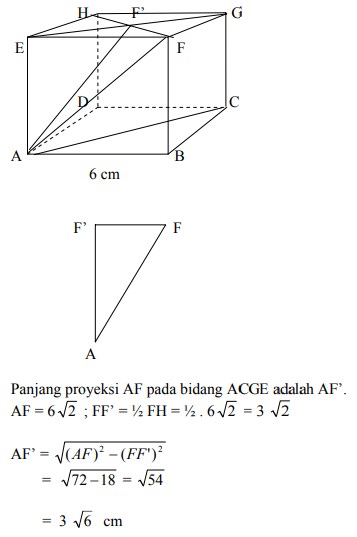
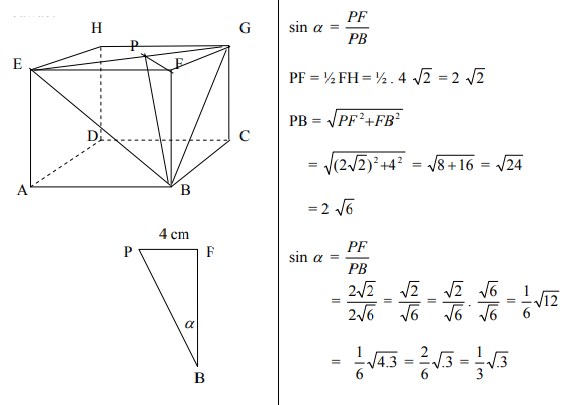
12. Perhatikan gambar kubus ABCD.EFGH di bawah ini. Panjang proyeksi AF pada bidang ACGE adalah….
A. 6 √3 cm
B. 6 √2 cm
C. 3 √6 cm
D. 3 √3 cm
E. 3 √2 cm
Jawaban :
Pembahasan :
Jawabannya adalah C
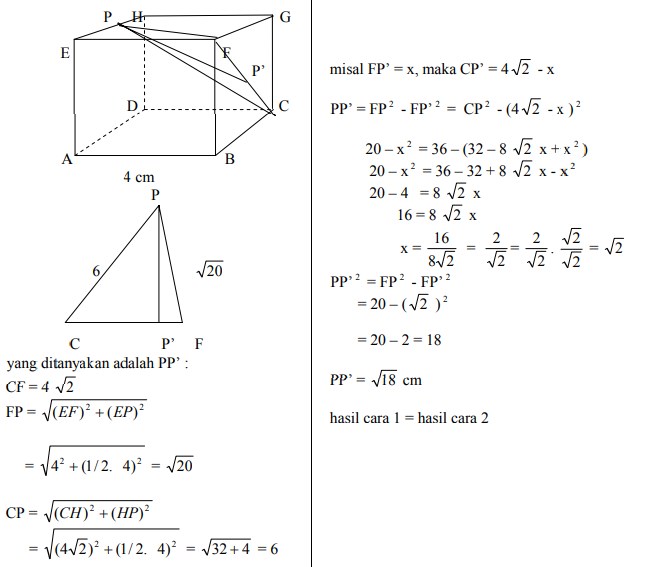
13. Diketahui kubus ABCD.EFGH dengan rusuk 4 cm. Jika P titik tengah EH, maka jarak titik P ke garis CF adalah…
A. √20 cm
B. √18 cm
C. √14 cm
D. √12 cm
E. √8 cm
Jawaban : B
Pembahasan :
Jawabannya adalah B
14. Panjang rusuk kubus ABCD.EFGH adalah 6 cm. Jarak titik C dengan bidang BDG adalah…
A. 2√2 cm
B. 2√3 cm
C. 3√2 cm
D. 3√3 cm
E. 4√3 cm
Jawaban :
Pembahasan :
Jawabannya adalah B
15. Pada kubus ABCD.EFGH besar sudut antara garis AH dan bidang diagonal BDHF adalah…
A. 30°
B. 45°
C. 60°
D. 75°
E. 90°
Jawaban : A
Pembahasan :
Jawabannya adalah A
Baca Juga : Soal Pythagoras
16. Diketahui kubus ABCD.EFGH dengan rusuk 4 cm. Jika sudut antara BF dan bidang BEG adalah α , maka sin α = ….
A. ¼√2
B. ½√2
C. 1/3√3
D. ½√3
E. ½√6
Jawaban : C
Pembahasan :
Jawabannya adalah C
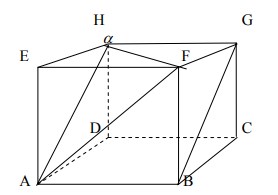
17. Besar sudut antara diagonal BG dan FH pada kubus ABCD.EFGH adalah …..
A. 30°
B. 45°
C. 60°
D. 75°
E. 90°
Jawaban : C
Pembahasan :
AH sejajar dengan BG, sehingga sudut antara diagonal BG dan FH adalah juga sudut antara diagonal AH dan FH (∠ (BG,FH) = ∠ (AH,FH) )
dari gambar terlihat bahwa panjang AH = AF = FH sehingga ∆ AFH adalah ∆sama sisi.
∆sama sisi. Mempunyai 3 sudut yang sama yaitu 60°
Jawabannya adalah C
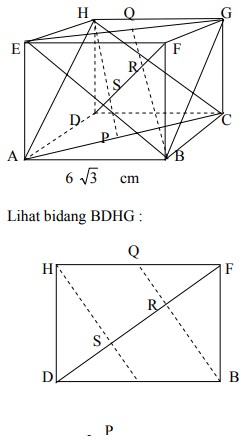
18. Jarak bidang ACH dan EGB pada kubus ABCD.EFGH dengan rusuk 6 3 cm adalah….
A. 4 √3 cm
B. 2 √3 cm
C. 4 cm
D. 6 cm
E. 12 cm
Jawaban : D
Pembahasan :
yang ditanya adalah jarak SR.
SR = DF – FR – DS
DF = 6 3 . 3 = 18 (diagonal ruang)
FR:
ingat titik berat ∆ = 1/3 tinggi
QR = 1/3 QB
DS :
∆ DSP sebangun dengan ∆FQR
sehingga DS = FR = 6
Kita cari dan buktikan :
PS = 1/3 PH
Sehingga panjang SR = DF – FR – DS
= 18 – 6 – 6 = 6 cm
Jawabannya adalah D
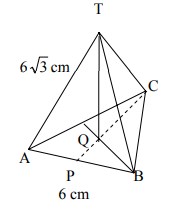
19. Diketahui limas segitiga beraturan T.ABC. Panjang rusuk AB= 6 cm, dan TA= 6√3 cm. Sudut antara TC dan bidang ABC adalah α , maka tan α = ….
A. 3√10
B. 4√2
C. 3√2
D. √10
E. 2√2
Jawaban : E
Pembahasan :
Karena limas segitiga beraturan maka:
panjang TA = TB = TC dan Bidangnya adalah segitiga sama sisi dengan panjang AB = BC = AC.
Sudut TC dan bidang ABC (∠TC, ABC) = ∠TCQ
Jawabannya adalah E
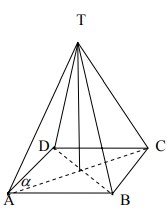
20. Pada limas segiempat beraturan T.ABCD yang semua rusuknya sama panjang. Sudut antara TA dan bidang ABCD adalah….
A. 15°
B. 30°
C. 45°
D. 60°
E. 75°
Jawaban : C
Pembahasan :
Misal panjang rusuk = a , maka
TA = TB = TB = TC = AB = BC = CD = AD = a
sudut antara TA dan bidang ABCD (∠ (TA,ABCD) ) adalah ∠ TAC
Jawabannya adalah C
Sudah selesai membaca dan berlatih soal ini ? Ayo lihat dulu Soal Matematika lainnya






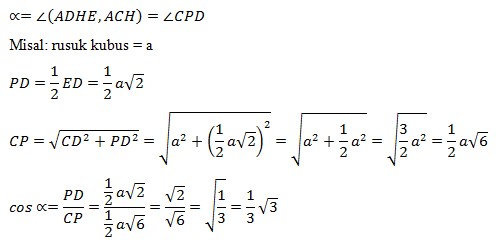
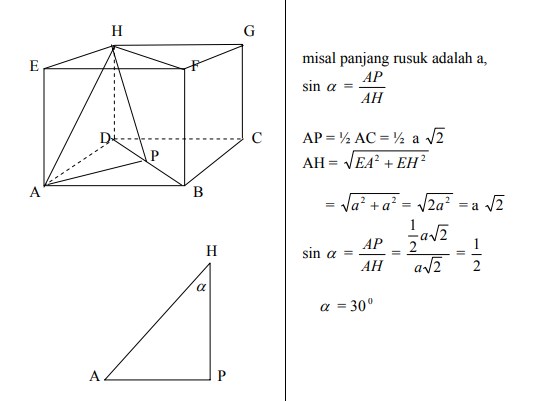
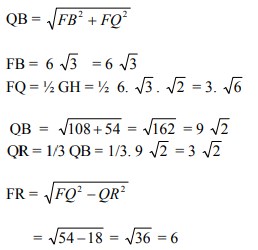






bidang diagonal yang melalui diagonal bidang EB adalah
Terimakasih ilmunya aangat bermanfaat. Saya izin menulisnya di buku catatan saya karena tugas dari gurus saya
Untyk soal no 7 kenapa jawaban dan cara sama seperti no 6?
Sudah diperbaiki, maaf ya kurang teliti.
Permisi Izin copas untuk tugas power point adik saya, terima kasih