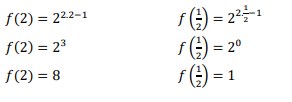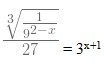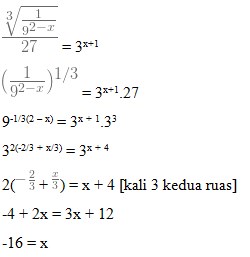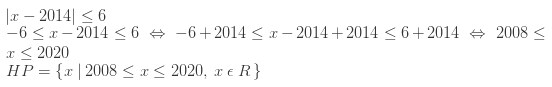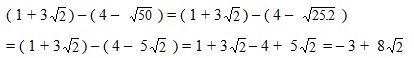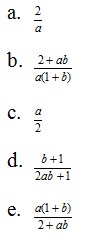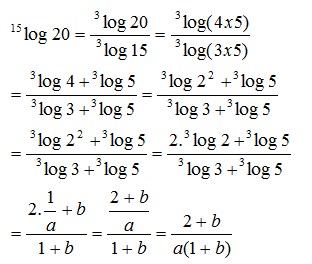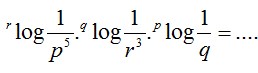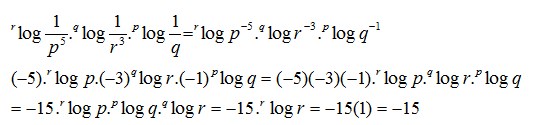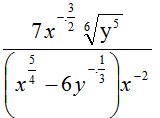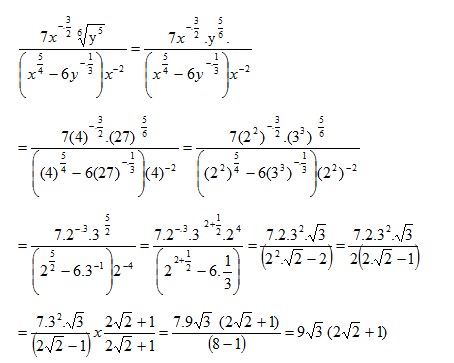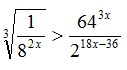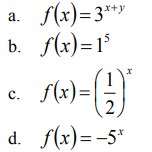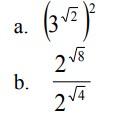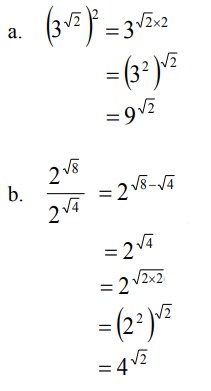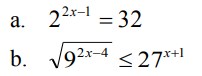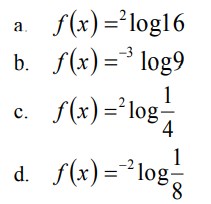30+ Soal Fungsi Eksponensial dan Jawaban

Contoh Soal Fungsi Eksponensial dan Jawaban – Bilangan Eksponen merupakan bentuk angka yang bersifat perkalian dengan angka yang sama sehingga kemudian angka tersebut dapat diulang dengan makna yang sama sebagai singkatnya dari perkalian.

Eksponensial selain dalam ilmu matematika sering digunakan dari berbagai bidang ekonomi, biologi, dan kimia selain itu juga sebagai ilmu komputer dengan aplikasi yang saling berhubungan pada kinerja ilmu matematika dan kimia. Fungsi Eksponensial dalam logaritma yang terkait dengan erat serta memiliki aplikasi penting dalam perekonomian yang berkaitan dengan masalah pertumbuhan yang di mana ekonomi secara umum.

Fungsi Eksponensial memiliki sifat sebagai berikut:

Sebagai Kurva yang terletak di atas sumbu x yang berfungsi sebagai bilangan yang positif

Sebagai bilangan yang dapat memotong sumbu y dengan titik ( 0,1 ).

dan sebagai Asimtot yang datar y  =  0 sebagai sumbu x dengan garis yang yang sejajar pada sumbu x.

Memiliki Grafik yang monoton naik pada bilangan x > 1.

Memiliki Grafik yang monoton turun pada bilangan 0 < x < 1.

Konsep :

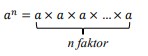
Dengan :

a = Bilangan pokok

n = Bilangan pangkat/eksponen

Sifat Bilangan Eksponensial.

Dengan 𝑎 > 0 dan 𝑎 ≠ 0

Fungsi eksponensial f dengan bilangan pokok a adalah fungsi yang memetakan setiap bilangan real x ke 𝑎𝑥 dengan 𝑎 > 0 dan 𝑎 ≠ 1 dan ditulis sebagai :

Bentuk pemetaan : f : 𝑥 → 𝑎^𝑥 , dengan 𝑎 > 0 dan 𝑎 ≠ 1 atau

Bentuk formula : 𝑓(𝑥) = 𝑎 𝑥 , dengan 𝑎 > 0 dan 𝑎 ≠ 1

Tahukah kamu dalam meningkatkan kemampuan matematika yang paling penting adalah banyak berlatih mengerjakan soal berikut ini contoh soal yang dapat kamu pelajari agar mudah mengerjakan soal yang lebih sulit.

1 – 10 Contoh Soal Fungsi Eksponensial dan Jawaban

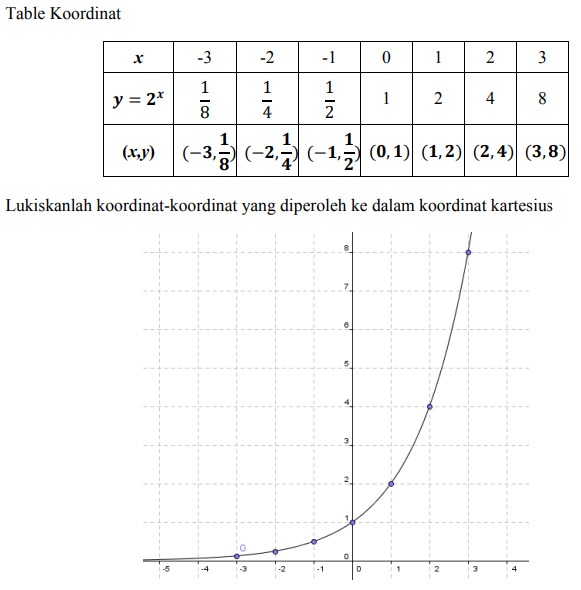
1. Diberikan 𝑓(𝑥) = 2^2𝑥−1 , carilah nilai dari 𝑓(2) dan 𝑓 ( ½ ) adalah. . .

Jawaban : 

2. Lukislah grafik fungsi 𝑦 = 2^𝑥 dengan 𝑥 ∈ R

Jawaban : 

3. Nilai x yang memenuhi persamaan

maka tentukanlah nilai x adalah . . .

A. -16

B. -7

C. 4

D. 5

E. 6

Jawaban : A

Pembahasan : 

4. √15 + √60 – √27 = …

Jawaban : 

√15 + √60 – √27

= √15 + √(4×15) – √(9×3)

= √15 + 2√15 – 3√3

= 3√15 – 3√3

= 3(√15 – √3)

5. Tentukanlah himpunan penyelesaian dari | x – 2014 | ≤ 6 

Jawaban : 

Simak Juga : Soal Persamaan Garis Lurus

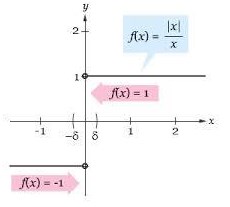
6. Gambarkanlah grafik 

untuk x bilangan real!

Jawaban :

dan seterusnya

Perhatikanlah ilustrasi berikut ini

7. Bentuk sederhana dari ( 1 + 3√2) – ( 4 – √50 ) adalah ….

A. – 2√2 – 3  

B. – 2√2 + 5

C. 8 √2 – 3     

D. 8 √2 + 3  

E. 8 √2 + 5

Jawaban : C

Pembahasan : 

8. Jika ²log 3 = a dan ³log 5 = b, maka ¹⁵log 20 = ….

Jawaban : B

Pembahasan : 

9. Tentukanlah :

maka nilai dari persamaan diatas adalah. . .

A. – 15

B. – 5

C. – 3

D. 1/15

E. 5

Jawaban : A

Pembahasan : 

10. Nilai dari :

untuk x = 4 dan y = 27 adalah ….

A. (1 + 2√2 ) 9√2

B. (1 + 2√2 ) 9√3

C. (1 + 2√2 ) 18√2

D. (1 + 2√2 ) 27√2

E. (1 + 2√2 ) 27√3

Jawaban : B

Pembahasan : 

11 – 20 Contoh Soal Fungsi Eksponensial dan Jawaban

11. Akar – akar persamaan 3^2x+1 – 28.3^x + 9 = 0 adalah x₁ dan x₂. Jika x1 > x2, maka nilai 3x₁ – x₂ = …

A. – 5

B. – 1

C. 4

D. 5

E. 7

Jawaban : E

Pembahasan : 

12. Akar – akar persamaan 2.3^4x – 20.3^2x + 18 = 0 adalah x₁ dan x₂. Nilai x₁ + x₂ = ….

A. 0

B. 1

C. 2

D. 3

E. 4

Jawaban : 

Pembahasan : 

Caranya sama dengan nomor 12, tetapi yang dimisalkan adalah 3^2x

Silahkan dicoba ya Soal Fungsi Eksponensial . . .

13. Nilai x yang memenuhi persamaan ²²log (2^x+1 + 3) = 1 + ²log x adalah ….

A. ²log 3

B. ³log 2

C. – 1 atau 3

D. 8 atau ½

E. log 2/3

Jawaban : A

Pembahasan : 

²log.²log (2^x+1 + 3) = 1 + ²log x

²log.²log (2^x+1 + 3) =  ²log 2 + ²log x

²log.²log (2^x+1 + 3) =  ²log 2x ( gunakan kesamaan pada logaritma )

²log (2^x+1 + 3) =  2x ( gunakan definisi logaritma sebagai invers eksponen ^alog b = c ↔ b= a^c )

2^x+1 + 3 =  2^2x  ( pindahkan semua nilai ke ruas kanan )

2^2x – 2^x+1 – 3 = 0

(2^x)² – 2^x.2¹ – 3 = 0

(2^x)² – 2.2^x – 3 = 0

Misal 2^x = q

q² – 2q – 3 = 0

( q – 3 ) ( q + 1 ) = 0

q – 3 = 0  atau  q + 1 = 0

q = 3 atau  q = –1

substitusikan nilai q pada 2^x = q

2^x = 3   atau 2^x = –1

x = ²log 3 (untuk 2^x = –1 tidak ada nilai x yang memenuhi, sebab hasil dari suatu bilangan yang dipangkatkan tidak pernah negatif )

14. Penyelesaian pertidaksamaan log (x – 4) + log (x + 8) < log (2x + 16) adalah ….

A. x > 6

B. x > 8

C. 4 < x < 6

D. – 8 < x < 6

E. 6 < x < 8

Jawaban :  C

Pembahasan Soal Fungsi Eksponensial : 

log (x – 4) + log (x + 8) < log (2x + 16)

log (x – 4) (x + 8) < log (2x + 16)

log ( x² + 4x – 32 ) < log ( 2x + 16 )  (gunakan kesamaan pada logaritma)

( x² + 4x – 32 ) < ( 2x + 16 )

x² + 4x – 32 – 2x – 16 < 0

x² + 2x – 48 < 0

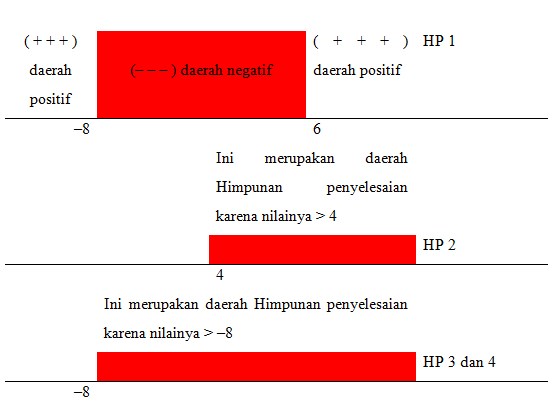
( x + 8 ) ( x – 6 ) < 0 (daerah Himpunan Penyelesaian ke – 1)

Cari harga pembuat nol untuk ( x + 8 ) dan ( x – 6 ), didapat x = –8  dan x = 6

Selain daerah penyelesaian diatas sebagai jawaban perlu juga dicek kembali nilai numerus untuk logaritmanya.

Untuk log (x – 4), nilai     x – 4 > 0

x > 4 ( daerah Himpunan Penyelesaian ke – 2 )

Untuk log (x + 8), nilai     x + 8 > 0

x > –8 ( daerah Himpunan Penyelesaian ke – 3 )

Untk log (2x + 16), nilai   2x + 16 > 0

 x > –8 ( daerah Himpunan Penyelesaian ke – 4 )

Cat : Untuk mendapatkan daerah positif atau negatif pada HP 1 caranya dengan substitusi nilai yang berada pada daerah tertentu, misalnya nilai yang kurang dari -8 ( misalnya diambil -9)

Substitusi nilai tersebut pada persamaan x² + 2x – 48

F(-9) = (-9)² + 2 (-9) – 48 = 81 – 18 – 48 = 15 ( didapat hasil yang positif )

Daerah yang memeuhi ketiga HP diatas adalah irisan dari ketiga HP tersebut, yaitu 4 < x < 6

15. Nilai x yang memenuhi pertidaksamaan : 2 log x log (2x + 5) + 2 log 2 adalah ….

A. -5/2 < x ≤ 8

B. -2 ≤ x ≤ 10

C. 0 < x ≤ 10

D. -2 < x < 0

E. -5/2 ≤ x < 0

Jawaban : C

Pembahasan : 

2 log x  log (2x + 5) + 2 log 2

log x²  log (2x + 5) + log 2²

log x²  log (2x + 5) ( 4 ) (gunakan kesamaan pada logaritma)

x²  (2x + 5) ( 4 )

x²  8x + 20

x² – 8x – 20  0

( x – 10 ) ( x + 2 )  0

Cari harga pembuat nol untuk ( x + 2 ) dan ( x – 10 ), didapat x = –2  dan x = 10

Selain daerah penyelesaian diatas sebagai jawaban perlu juga dicek kembali nilai numerus untuk logaritmanya.

Untuk log x, nilai   x > 0   (daerah Himpunan Penyelesaian ke – 2 )

Untuk log ( 2x + 5 ), nilai  2x + 8 > 0  x > – ⁵/₂  ( daerah Himpunan Penyelesaian ke – 3 )

Daerah yang memeuhi ketiga HP diatas adalah irisan dari ketiga HP tersebut, yaitu 0 < x ≤ 10

Lihat Juga : Contoh Soal Bilangan Palindrom

16. Himpunan penyelesaian persamaan 2.9^x – 3^x+1 + 1 = 0 adalah ….

A. { ½ , 1 }

B. { –½ , –1 }

C. { –½ , 1 }

D. { 0 , ³log ½ }

E. { ½ , ^½log 3 }

Jawaban : 

Pembahasan : 

Caranya sama dengan sebelumnya, tetapi yang dimisalkan adalah 3^2x.

17. Nilai x yang memenuhi pertidaksamaan :

maka hasilnya adalah …

A. x < –14

B. x < –15

C. x < –16

D. x < –17

E. x < –18

Jawaban : E

Pembahasan : 

18. Himpunan penyelesaian persamaan ^xlog ( 10x³ – 9x ) = ^xlog x⁵ adalah ….

A. { 3 }

B. { 1,3 }

C. { 0,1,3 }

D. { –3, –1,1,3 }

E. { –3, –1,0,1,3 }

Jawaban : B

Pembahasan : 

^xlog ( 10x³ – 9x ) = ^xlog x⁵   (gunakan kesamaan pada logaritma )

10x³ – 9x = x⁵

x⁵ – 10x³ + 9x = 0  (faktorkan dengan mengeluarkan variabel x)

x ( x⁴ – 10x² + 9 ) = 0 ( faktorkan kembali persamaan yang ada didalam kurung )

x ( x² – 9 ) ( x² – 1 ) = 0  ( faktorkan kembali persamaan yang ada didalam kurung )

x ( x – 3 ) ( x  + 3 ) ( x – 1 ) ( x  + 1 ) = 0

Cari harga pembuat nol untuk x, ( x – 3 ), ( x  + 3 ), ( x – 1 ) dan ( x  + 1 ).

Didapat    

x = 0

x = 3

x = –3 

x = 1

x = –1

Dari kelima jawaban hanya 1 dan 3 yang memenuhi persyaratan jika disubstitusikan kepersamaan ( ingat kembali syarat dari bilangan pokok logaritma )

19. Nilai x yang memenuhi 3^x²-3x+4 adalah ….

A. 1 < x < 2

B. 2 < x < 3

C. –3 < x < 2

D. –2 < x < 3

E. –1 < x < 2

Jawaban Soal Fungsi Eksponensial : B

Pembahasan : 

20. Jika x₁ dan x₂ adalah akar – akar persamaan (³log x)² – 3.³log x + 2 = 0, maka x₁.x₂ = ….

A. 2

B. 3

C. 8

D. 24

E. 27

Jawaban : E

Pembahasan : 

(³log x)² – 3.³log x + 2 = 0

Misal ³log x = p

p² -3p + 2 = 0

( p – 2 ) ( p – 1 ) = 0

p₁ = 2 atau p₂ = 1

³log x₁ =  2  atau  ³log x₂ = 1

x₁ = 9  atau x₂ = 3

x₁ . x₂ = 27

21 – 30 Contoh Soal Fungsi Eksponensial dan Jawaban

Soal Essay

21. Perhatikan fungsi berikut, manakah yang merupakan fungsi eksponen dan yang bukan merupakan fungsi eksponesial serta berikan alasannya :

Jawaban :

Pembahasan : 

22. Tuliskan bentuk yang paling sederhana dari :

Jawaban :

Pembahasan : 

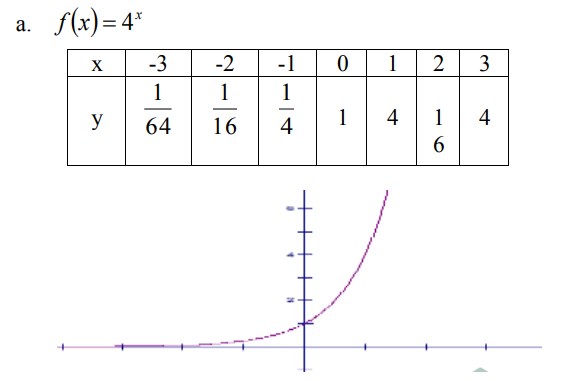
23. Gambarkan grafik fungsi f (x)  = 4^x adalah. . .

Jawaban :

Pembahasan : 

24. Tentukanlah nilai x yang memenuhi untuk :

Jawaban :

Pembahasan : 

25. Pada awal tahun, Adam menabung uang di bank sebesar Rp1.000.000,00. Ia menyimpan uang tersebut selama 48 bulan. Jika bank memberi suku bunga majemuk 10% setahun, tentukan:

a. Model persamaannya

b. Jumlah uang Adam pada akhir tahun keempat.

Jawaban :

Pembahasan : 

Diketahui :

M = Rp1.000.000,00

i = 10% = 0,1

n = 4 Tahun

Ditanyakan :

a. Model persamaannya

b. Jumlah uang Adam pada akhir tahun keempat

Penyelesaian :

Jadi, jumlah uang Adam pada akhir tahun keempat adalah Rp1.464.100,00

Simak Juga : Contoh Soal Fungsi Komposisi dan Invers

26. Perhatikan fungsi berikut, manakah yang merupakan fungsi logaritma dan yang bukan merupakan fungsi logaritma serta berikan alasannya :

Jawaban :

Pembahasan : 

26. Ubahlah : 

Jawaban :

Pembahasan : 

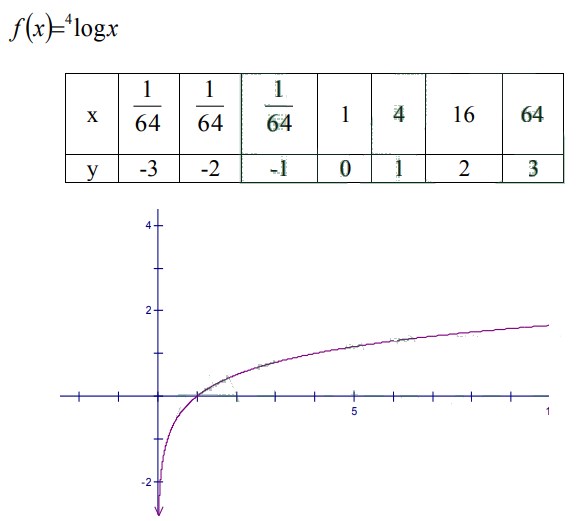
28. Gambarkan grafik fungsi f (x) = ⁴log x adalah. . .

Jawaban :

Pembahasan : 

29. Tentukanlah nilai x yang memenuhi untuk:

a. ³log( x – 3) = ³log(2x – 7)

b. ²log(x – 1) < 2

Jawaban :

Pembahasan : 

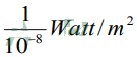
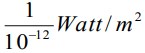
30. Sebuah sumber bunyi mempunyai Intensitas bunyi sebesar Jika Intensitas ambang pendengaran  Tentukan:

a. Model persamaannya

b. Besar taraf intensitas bunyi tersebut

Jawaban :

Pembahasan : 

Sudah selesai membaca dan berlatih soal ini ? Ayo lihat dulu Soal Matematika lainnya

Sekarang sudah banyak Blog Edukatif dimana blog yang di desain sebagai media pembelajaran maupun sumber belajar. Isinya bisa luas menyangkut banyak kegiatan belajar yang dapat membuat siswa lebih mandiri dalam mencari ilmu.

Posting terkait:

Contoh Soal Barisan dan Deret Aritmatika [Update 50 Butir]

Contoh Soal Lingkaran Kelas 8 SMP dan Jawaban [Update]

65+ Contoh Soal Limit Fungsi Aljabar dan Jawaban [Update]