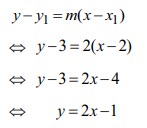Contoh Soal Persamaan Garis Lurus dan Jawaban – Persamaan garis lurus dapat didefinisikan dengan persamaan linier yaitu ada yang terdiri dari satu variabel dan ada juga yang terdiri dari dua variabel.

Persamaan Garis lurus merupakan suatu perbandingan antara koordinat y dan koordinat x dari dua titik yang terletak pada sebuah garis. Sedangkan garis lurus sendiri adalah kumpulan dari titik – titik yang sejajar. Dan garis lurus dapat dinyatakan dalam berbagai bentuk.
Dibawah ini beberapa contoh untuk menyatakan persamaan garis lurus, yaitu :
y = mx
y = -mx
y = a
x = a
ax + by = ab
ax – by = -ab
dan lain-lain
Persamaan garis lurus selalu berkaitan dengan gradien. Gradien adalah Perbandingan komponen y dan komponen x , atau disebut juga dengan kecondongan sebuah garis. Lambang dari suatu gradien yaitu huruf “m”.
Gradien juga dapat dinyatakan sebagai nilai dari kemiringan suatu garis dan dapat dinyatakan dengan perbandingan Δy/Δx
1 – 10 Contoh Soal Persamaan Garis Lurus dan Jawaban
1. Diketahui titik-titik pada bidang koordinat Cartesius sebagai berikut.
a. (10, –5)
b. (2, 8)
c. (–7, –3)
d. (6, 1)
e. (–4, 9)
Tentukan absis dan ordinat dari masing-masing titik tersebut.
Jawaban :
a. Dari titik (10, –5) diperoleh absis: 10, ordinat: –5
b. Dari titik (2, 8 ) diperoleh absis: 2, ordinat: 8
c. Dari titik (–7, –3) diperoleh absis:–7, ordinat: –3
d. Dari titik (6, 1) diperoleh absis: 6, ordinat: 1
e. Dari titik (–4, 9) diperoleh absis:–4, ordinat: 9
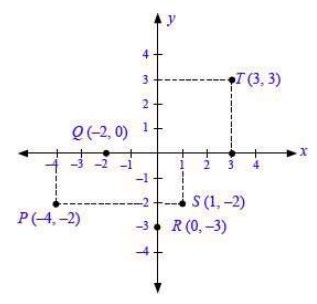
2. Gambarlah titik-titik berikut pada bidang koordinat Cartesius.
a. P (–4,–2)
b. Q (–2, 0)
c. R (0, –3)
d. S (1, –2)
e. T (3, 3)
Jawaban :
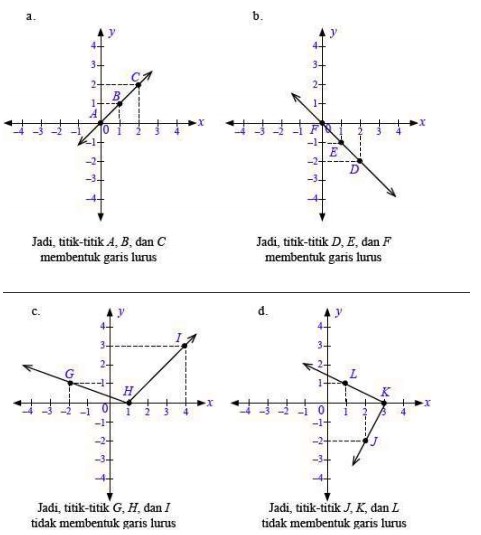
3. Tentukan apakah titik-titik berikut membentuk garis lurus atau tidak….
a. A(0, 0), B(1, 1), C(2, 2)
b. D(2, –2), E(1, –1), F(0, 0)
c. G(–2, 1), H(1, 0), I(4, 3)
d. J(2, –2), K(3, 0), L(1, 1)
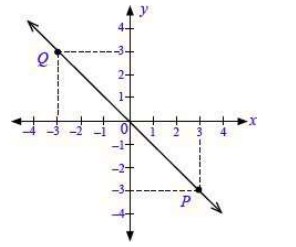
Gambarkanlah garis lurus yang melalui titik P(3, –3) dan Q(–3, 3) . . .
Jawaban :
Garis lurus yang melalui titik P(3, –3) dan Q(–3, 3) dapat digambar sebagai berikut.
4. Gambarlah garis dengan persamaan:
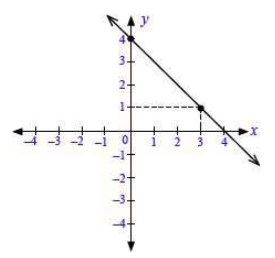
a. x + y = 4,
b. x = 2y
Jawaban :
a. Langkah pertama adalah menentukan nilai x dan y yang memenuhi persamaan x + y = 4.
→ y = 4, sehingga diperoleh titik koordinat (0, 4), ⇒ Misalkan: x = 0 maka 0 + y = 4
→ y = 1, sehingga diperoleh titik koordinat (3, 1). ⇒ x = 3 maka 3 + y = 4
Kemudian, dari dua titik koordinat tersebut dapat digambarkan garis lurus seperti berikut.
b. Seperti sebelumnya, tentukan dahulu nilai x atau y yang memenuhi persamaan x = 2y.
→ y = 0, sehingga diperoleh titik koordinat (0, 0), ⇒ Misalkan: x = 0 maka 0 = 2y
→ y = 2, sehingga diperoleh titik koordinat (4, 2) ⇒ x = 4 maka 4 = 2y
Kedua titik tersebut dapat digambar menjadi sebuah garis lurus sebagai berikut
5. Tentukanlah gradien dari persamaan garis berikut.
a. y = 2x
b. y = 3x
c. x = 2y
d. 2x + 3y = 0
e. 4x – 6y = 0
Jawaban :
a. Persamaan garis y = 2x sudah memenuhi bentuk y = mx. Jadi, diperoleh m = 2.
b. Persamaan garis y = –3x sudah memenuhi bentuk y = mx. Jadi, diperoleh m = –3.
c. Persamaan garis x = 2y diubah terlebih dahulu menjadi bentuk y = mx sehingga
Simak Juga : Soal Bilangan Palindrom
6. Tentukanlah gradien dari persamaan garis berikut.
a. y = 4x + 6
b. y = –5x – 8 c. 2y = x + 12
d. 3y = 6 + 9x
e. 2 + 4y = 3x + 5
Jawaban :
a. Persamaan garis y = 4x + 6 sudah memenuhi bentuk y = mx + c. Jadi, nilai m = 4.
b. Persamaan garis y = –5x – 8 sudah memenuhi bentuk y = mx + c. Jadi, nilai m = –5.
c. Persamaan garis 2y = x + 12 diubah terlebih dahulu menjadi bentuk y = mx + c sehingga
7. . Tentukan persamaan garis untuk garis yang melalui titik O (0, 0) dan memiliki:
a. gradien 2,
b. gradien –3,
c. gradien 1.
Jawaban :
y = 2x ⇒ a. y = mx maka y = (2)x
y = –3x ⇒ b. y = mx maka y = (–3)x
y = x ⇒ c. y = mx maka y = (1)x
8. Tentukan persamaan garis yang melalui titik P(3, 5) dan memiliki gradien –2.
Jawaban :
Untuk titik P(3, 5) maka x1 = 3, y1 = 5.
Dengan menggunakan rumus umum, diperoleh persamaan garis:
fi y – y1 = m (x – x1)
y – 5 = –2 (x – 3)
y – 5 = –2x + 6
y = –2x + 6 + 5
y = –2x + 11 atau 2x + y – 11 = 0
9. Tentukan persamaan garis yang melalui titik K(–2, –4) dan sejajar dengan garis 3x + y – 5 = 0 adalah . . .
Jawaban :
Langkah pertama, tentukan gradien garis 3x + y – 5 = 0.
3x + y – 5 = 0
y = –3x + 5
diperoleh m = –3.
Oleh karena garis h sejajar dengan garis 3x + y – 5 = 0 maka garis h
memiliki gradien yang sama, yaitu m = –3.
Garis h melalui K(–2, –4) maka x1 = –2, y1 = –4.
Langkah kedua, tentukan persamaan garis h sebagai berikut
y – y1 = m (x – x1)
y – (–4) = –3(x – (–2))
y + 4 = –3x – 6
y = –3x – 6 – 4
y = –3x –10
Jadi, persamaan garis h adalah y = –3x – 10 atau 3x + y + 10 = 0
10. Dengan cara substitusi, tentukan koordinat titik potong antara garis 3x + y = 5 dan garis 2x – 3y = 7.
Jawaban :
Ikuti langkah-langkah berikut.
Ambil salah satu persamaan garis, misalnya 3x + y = 5.
Tentukan salah satu variabel dari garis tersebut, misalnya y.
3x + y = 5 maka y = 5 – 3x.
Substitusikan nilai y tersebut ke dalam persamaan garis yang lain.
2x – 3y = 7
2x – 3(5 – 3x) = 7
2x – 15 + 9x = 7
2x + 9x = 7 + 15
11x = 22
x = 2
Substitusikan nilai x ke dalam salah satu persamaan garis.
3x + y = 5
3 (2) + y = 5
6 + y = 5
y = 5 – 6
y = –1
Diperoleh x = 2 dan y = –1. Jadi, koordinat titik potong kedua garis itu adalah (2, –1)
11 – 20 Soal Persamaan Garis Lurus dan Jawaban
11. Diketahui persamaan garis y = 3x + 5 , tentukan gradien garis tersebut, kemudian tentukan gradien garis h yang sejajar dengan garis y = 3x + 5 .
Jawaban :
Gradien garis y = 3x + 5 adalah 3. Maka gradien garis h yang sejajar dengan garis y = 3x + 5 adalah 3.
12. Diketahui garis p tegak lurus dengan garis q. Jika gradien garis p adalah -4/5 tentukan gradien garis q
Jawaban :
Misalkan gradien garis p adalah ݉mp dan gradien garis q adalah ݉pq, maka
berlaku :
13. Diketahui garis g melalui titik (-1,5) dan titik (2,-4) dan garis h melalui titik (3,-2) dan (6,-1). Selidiki apakah garis g tegak lurus garis h.
Jawaban :
14, Tentukan persamaan garis lurus yang melalui titik (4, – 3) dan bergradien -3/5.
Jawaban :
15. Tentukan persamaan garis lurus yang melalui titik P(-4, 3) dan Q(3,-2)
Jawaban :
Lihat Juga : Soal Unsur, Keliling, dan Luas Lingkaran
16. Diketahui garis h melalui titik A(-3 , 2) dan titik B (a,5). Tentukanlah nilai a jika gradien garis h adalah 3/7 . Kemudian tentukan persamaan garis h tersebut.
Jawaban :
Untuk menyelesaikan permasalahan tersebut langkah-langkahnya adalah:
17. Tentukan gradien garis dengan persamaan 5/4 x – 6 adalah. . .
Jawaban :
18. Tentukan gradien garis dengan persamaan 5x + 2y – 7 = 0 adalah. . .
Jawaban :
Untuk menentukan gradien dari garis dengan persamaan berbentuk 5x + 2y – 7 = 0 dapat diselesaikan dengan cara:
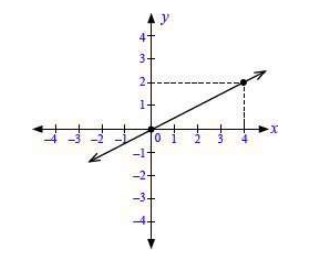
19. Tentukan persamaan garis yang melalui titik (2,3) dan sejajar dengan garis y = 2x – 5 adalah. . .
Jawaban :
Gradien garis y = 2x – 5 adalah 2, maka gradien garis yang sejajar dengan garis y = 2x – 5 sama dengan 2. Persamaan garis yang melalui (2,3) dan dengan gradien 2 adalah :
Jadi persamaan garis yang melalui (2,3) dan sejajar dengan garis y = 2x – 5 adalah y = 2x – 1.
20. Tentukan persamaan garis yang melalui titik (6,3) dan sejajar garis dengan persamaan 4x + 3y – 6 = 0 adalah . . .
Jawaban :
Jadi persamaan garis yang melalui (6,3) dan sejajar dengan garis 4x + 3y – 6 = 0 adalah 4x + 3y – 33 = 0
21 – 30 Contoh Soal Persamaan Garis Lurus dan Jawaban
21. Tentukan persamaan garis g yang melalui titik A(-4,3) dan sejajar dengan garis h dengan persamaan 3y = -5x + 6 .
Jawaban :
Untuk menyelesaikan permasalahan tersebut langkah-langkahnya sebagai berikut.
22. Diketahui garis h = y = -3x + 1 dan garis k = y = 3x – 5 berpotongan di titik A. Garis l melalui titik A sejajar dengan garis g = y = 4x + 8. Jika garis l memotong sumbu y di titik (0, a) tentukanlah nilai ܽa adalah . . .
Jawaban :
23. Tentukan persamaan garis k yang melalui titik ( -5, 3 ) dan tegak lurus dengan garis l ≡ 4y +5x -6 adalah. . .
Jawaban :
24. Diketahui garis g melalui titik A(0,b) dan titik B(4,7). Tentukan nilai b jika garis g tegak lurus dengan garis h yang persamaannya 3y – 4x – 6. Kemudian tentukan persamaan garis g.
Jawaban :
karena garis g melalui titik A(0,4) dan titik B(4,7), maka persamaan garis g adalah sebagai berikut.
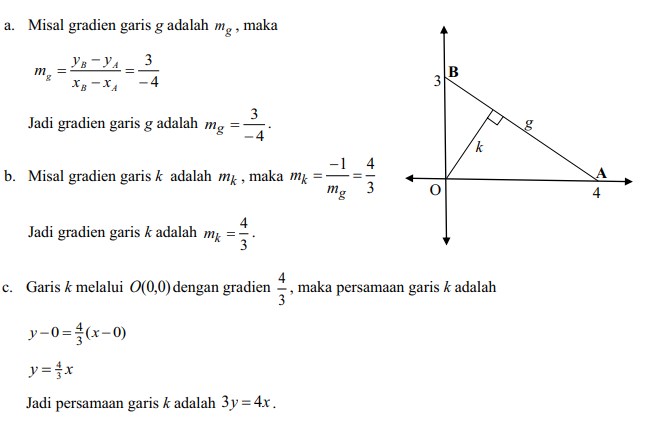
25. Diketahui garis g memotong sumbu x di A(4,0) dan sumbu y di B(0,3). Garis k melalui titik O(0,0) dan tegak lurus pada garis g. Tentukan:
(a) gradien garis g
(b) gradien garis k
(c) persamaan garis k
Jawaban :
Untuk menyelesaikan soal tersebut siswa diminta menggambar grafiknya seperti pada Gambar :
Baca Juga : Soal Turunan Fungsi Aljabar
26. Tentukan hubungan antara garis dengan persamaan l1 ≡ 3x – 4y – 7 = 0 dan ݈l2 ≡ 6x – 8y – 14 = 0 adalah . . .
Jawaban :
Untuk menentukan hubungan kedua garis tersebut, maka ditentukan hubungan antara koefisien x , koefesien y dan konstantanya.
Sudah selesai membaca dan berlatih soal ini ? Ayo lihat dulu Soal Matematika lainnya