Contoh Soal Persamaan Kuadrat dan Jawaban – Dalam aljabar, persamaan kuadrat adalah setiap persamaan yang dapat disusun ulang dalam bentuk standar karena x mewakili suatu yang tidak diketahui, dan a, b, dan c mewakili angka yang diketahui, di mana a 0. Jika a = 0, maka persamaannya adalah linear, tidak kuadratik, karena tidak ada istilah.

Persamaan kuadrat merupakan suatu persamaan dari variabel yang mempunyai pangkat tertinggi yaitu 2. pada umumnya Metode rumus abc biasa digunakan jika pemfaktoran dan melengkapkan kuadrat sempurna tidak bisa dilakukan.
Rumus abc
Metode yang paling umum untuk menyelesaikan persamaan kuadrat ax2 + bx + c = 0 dengan menggunakan rumus kuadrat atau sering disebut rumus abc.
Rumus kuadrat diperoleh dengan proses melengkapkan kuadrat sempurna untuk persamaan kuadrat .
Prosesnya sebagai berikut :
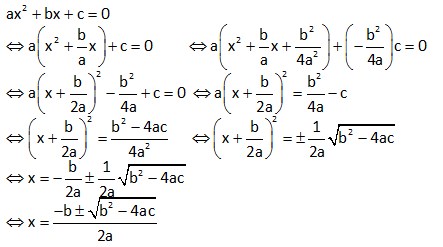
1 – 10 Soal Persamaan Kuadrat dan Jawaban
1. Tentukan himpunan penyelesaian dari persamaan kuadrat berikut dengan cara memfaktorkan !
a) x2 − x – 20 = 0
b) 2x2 + 5x − 3 = 0
c) X2 – 25 = 0
d) (x – 2)2 = x – 2
Jawaban :
Pembahasan :
2. Tentukan himpunan penyelesaian dari persamaan kuadrat berikut dengan melengkapkan kuadrat sempurna!
a) x2 – 6 x + 5 = 0.
b) x2 – 6 x + 8 = 0.
c) x2 -2 x -24 = 0
Jawaban :
Pembahasan :
3. Selesaikanlah persamaan kuadrat berikut dengan memakai rumus!
a) x2 + x – 30 = 0
b) x2 – 2 x – 24 = 0
c) x2 + 4x – 12 = 0
Jawaban :
Pembahasan :
4. Tentukan jenis akar persamaan kuadrat x2 + 5x + 2 = 0 tanpa menyelesaikan persamaannya!
Jawaban :
Pembahasan :
Ternyata D > 0. Jadi, persamaan x2 + 5x + 2 = 0 mempunyai dua akar real berlainan
5. Tentukan jenis akar persamaan kuadrat x2 – 6 x + 9 = 0 tanpa menyelesaikan persamaannya!
Jawaban :
Pembahasan :
Ternyata D = 0. Jadi, persamaan x2 − 6x + 9 = 0 mempunyai dua akar real dan kembar (sama)
6. Tentukan nilai p agar persamaan kuadrat 4x2 + 8px + 1 = 0 mempunyai akar yang sama (kembar)!
Jawaban :
Pembahasan :
7. Tanpa menyelesaikan persamaan terlebih dahulu, tentukan jenis akar persamaan kuadrat dari x2 – 10 x + 25 = 0
Jawaban :
Pembahasan :
Karena D = 0, maka persamaan x2 – 10x + 25 = 0 mempunyai dua akar real sama.
8. Tanpa menyelesaikan persamaan terlebih dahulu, tentukan jenis akar persamaan kuadrat dari 3x2 – 4 x + 2 = 0 !
Jawaban :
Pembahasan :
Ternyata bahwa D < 0. Jadi, persamaan 3x2 – 4 x + 2 = 0 tidak mempunyai akar real.
9. Jika x1 dan x2 adalah akar-akar persamaan kuadrat x2 – 3x + 2 = 0, maka tanpa harus menyelesaikan persamaannya, hitunglah :
a) x1 + x2
b) x1 . x2
Jawaban :
Pembahasan :
10. Jika p dan q akar-akar persamaan kuadrat x2 + 5x + 6 = 0. Tentukan nilai: p2 + q2 adalah . . .
Jawaban :
Pembahasan :
11 – 20 Soal Persamaan Kuadrat Beserta Pembahasan
11. Persamaan kuadrat x2 – 5x + 6 = 0 mempunyai akar – akar x1 dan x2. Persamaan kuadrat yang akar – akarnya x1 – 3 dan x2 – 3 adalah …
A. x2 – 2x = 0
B. x2 – 2x + 30 = 0
C. x2 + x = 0
D. x2 + x – 30 = 0
E. x2 + x + 30 = 0
Jawaban : C
Pembahasan :
akar – akarnya :
x1 – 3 = y ⇒ x1 = y + 3
x2 – 3 = y ⇒ x2 = y + 3
Substitusi nilai “x1” atau “x2” kepersamaan kuadrat dalam soal, sehingga menjadi :
x2 – 5x + 6 = 0
PK Baru :
(y + 3)2 – 5(y + 3) + 6 = 0
y2 + 6y + 9 – 5y – 15 + 6 = 0
y2 + y = 0
12. Pak dedi mempunyai kebun berbentuk persegi panjang dengan luas 192 m2. Selisih panjang dan lebarnya adalah 4 m. Apabila disekeliling kebun dibuat jalan dengan lebar 2 m, maka luas jalan tersebut adalah … m2.
A. 96
B. 128
C. 144
D. 156
E. 168
Jawaban : A
Pembahasan :
p – l = 4
p x l = 192
(4 + l) x l = 192
4l + l2 = 192
l2 + 4l – 192 = 0
(l – 12)(l + 16) = 0
l = 12 atau l = -16 (tidak memenuhi)
p = 4 + l = 4 + 12 = 16
Untuk menentukan luas jalan, kita partisi-partisi menjadi 8 yaitu :
4 luas jalan yang berada di pojok-pojok kebun berbentuk persegi dengan panjang sisi 2cm : 4 x 22 = 16cm2
2 luas jalan yang berada pada panjang kebun dengan panjang sisi 12cm dan lebar 2cm : 2 x (12 x 2) = 48cm2
2 luas jalan yang berada pada lebar kebun dengan panjang sisi 8cm dan lebar 2cm : 2 x (8 x 2) = 32cm2
Jadi luas jalan yang dibangun adalah 16 + 48 + 32 = 96cm2
13. Persamaan 2x2 + qx + (q – 1) = 0 mempunyai akar – akar x1 dan x2. Jika x12 + x22 = 4, maka nilai q = …
A. -6 dan 2
B. -6 dan -2
C. -4 dan 4
D. -3 dan 5
E. -2 dan 6
Jawaban : E
Pembahasan :
x12 + x22 = 4
(x1 + x2)2 – 2x1x2 = 4
(-b/a)2 – 2(c/a) = 4
(-q/2)2 – 2((q – 1)/2) = 4
q2/4 – q + 1 = 4 (kalikan 4)
q2 – 4q + 4 = 16
q2 – 4q – 12 = 0
(q – 6)(q + 2) = 0
q = 6 atau q = -2
14. Jika nilai diskriminan persamaan kuadrat 2x2 – 9x + c = 0 adalah 121, maka c = …
A. -8
B. -5
C. 2
D. 5
E. 8
Jawaban : B
Pembahasan :
D = 121
b2 – 4ac = 121
(-9)2 – 4(2)(c) = 121
81 – 8c = 121
81 – 121 = 8c
-40 = 8c
-5 = c
15. Persamaan (1 – m)x2 + (8 – 2m)x + 12 = 0 mempunyai akar kembar, maka nilai m = …
A. -2
B. -3/2
C. 0
D. 3/2
E. 2
Jawaban : A
Pembahasan :
Akar kembar jika D = 0
b2 – 4ac = 0
(8 – 2m)2 – 4(1 – m)(12) = 0
64 – 32m + 4m2 – 48 + 48m = 0
4m2 + 16m + 16 = 0
4(m2 + 4m + 4) = 0
(m + 2)(m + 2) = 0
m1,2 = -2
16. Suatu fungsi kuadrat mempunyai nilai minimum –2 untuk x = 3 dan untuk x = 0 nilai fungsi 16. Fungsi kuadrat itu adalah …
Jawaban :
misal : f(x) = ax2 + bx + c
substitusi x = 0 untuk nilai fungsi 16, sehingga :
f(0) = a(0)2 + b(0) + c
16 = c … (i)
Substitusi x = 3 untuk nilai minimum -2, sehingga :
f(3) = a(3)2 + b(3) + c
-2 = 9a + 3b + c … (ii)
f'(x) = 2ax + b
substitusi titik x = 3 (titik minimum) untuk f'(x) = 0, sehingga :
0 = 2a(3) + b
b = -6a … (iii)
substitusi (i) dan (iii) ke (ii), sehingga diperoleh :
-2 = 9a + 3b + c
-2 = 9a + 3(-6a) + 16
-2 = 9a – 18a + 16
-18 = -9a
2 = a
b = -12
f(x) = ax2 + bx + c
substitusi a = 2 , b = -12 dan c = 16
f(x) = 2x2 – 12x + 16
17. Grafik fungsi kuadrat f(x) = x² + bx + 4 menyinggung garis y = 3x + 4. Nilai b yang memenuhi adalah . . .
A. – 4
B. – 3
C. 0
D. 3
E. 4
Jawaban : D
Pembahasan
Karena garis dan grafik bersinggungan, maka berlaku:
x² + bx + 4 = 3x + 4
x² + (b – 3) x = 0
Menggunakan sifat garis singgung grafik fungsi kuadrat, maka berlaku nilai diskriminan (D) pada persamaan adalah 0, sehingga:
(b – 3)² – 4 ⋅ 1 ⋅ 0 = 0 ⇔ (b – 3)² = 0 ⇔ b = 3
18. Grafik y = px2 + (p + 2)x – p + 4 memotong sumbu x di dua titik. Batas – batas nilai p yang memenuhi adalah…
A. p < -2 atau p > – 2/5
B. p < 2/5 atau p > 2
C. p < 2 atau p > 10
D. 2/5 < p < 2
E. 2 < p < 10
Jawaban : B
Pembahasan :
Syarat memotong : D > 0
19. Persamaan kuadrat x2 + (m – 2)x + 2m – 4 = 0 tidak mempunyai akar – akar real. Batas – batas nilai m yang memenuhi adalah…
A. m ≤ 2 atau m ≥ 10
B. m ≤ -10 atau m ≥ -2
C. m < 2 atau m > 10
D. m < 2 atau m < 10
E. m < 2 atau m ≤ 10
Jawaban : D
Pembahasan :
Metode supertrik :
Tidak mempunyai akar – akar real : D < 0, artinya pilih KECIL < x < BESAR (jadi pilihan A,B,C jelas salah)
20. Persamaan kuadrat 2x2 – 2(p – 4)x + p = 0 mempunyai dua akar real berbeda. Batas – batas nilai p yang memenuhi adalah…
A. p ≤ 2 atau p ≥ 8
B. p < 2 atau p > 8
C. p < – 8 atau p > 2
D. 2 ≤ p ≤ 8
E. -8 ≤ p ≤ -2
Jawaban : B
Pembahasan :
Metode supertrik :
Akar – akar real berbeda : D > 0 artinya pilih KECIL atau BESAR (pilihan D dan E jelas salah)
21 – 30 Soal Persamaan Kuadrat dan Pembahasan
21. Grafik fungsi kuadrat f(x) = x2 + (t + 3)x + t – 1 memotong garis y = – 4 di dua titik yang berlainan. Batas – batas nilai t adalah…
A. -1 < t < 3
B. -3 < t < 1
C. -3 < t < -1
D. t < -3 atau t > 3
E. t ≤ -1 atau t ≥ 3
Jawaban : D
Pembahasan soal persamaan kuadrat :
Memotong : D > 0
y = y sehingga diperoleh :
22. Akar-akar persamaan kuadrat 5x2 – 3x + 1 = 0 adalah …
A. imajiner
B. kompleks
C. nyata, rasional dan sama
D. nyata dan rasional
E. nyata, rasional dan berlainan.
Pembahasan:
NOTE :
D > 0, memiliki akar-akar riil dan berbeda
D < 0, memiliki akar-akar imajiner
D = 0, memiliki akar-akar riil dan kembar
D = b2 – 4ac
= (-3)2 – 4.5.1
= 9 – 20
= -11
Jawaban : A
23. Diberikan persamaan kuadrat sebagai berikut:
2x2 + x − 6 = 0
Faktorkan persamaan-persamaan di atas dengan menggunakan Rumus ABC!
A. -2
B. -1
C. 0
D. 1
E. 2
Jawaban : A
Pembahasan :
Menggunakan Rumus ABC
24. Hasil kali akar-akar persamaan kuadrat 6x2 – 2x + 3 = 0 adalah …
A. 3
B. 2
C. 1/2
D. –1/2
E. -2
Jawaban : C
Pembahasan :
6x2 – 2x + 3 = 0
x1.x2 = c/a
= 3/6
= 1/2
25. Akar-akar persamaan kuadrat x2 + 3x – 2 = 0 adalah x1 dan x2. Nilai + = …
A. –2/3
B. –3/2
C. 2/3
D. 3/2
E. 5/2
Jawaban : D
Pembahasan Soal Persamaan Kuadrat :
26. Akar-akar persamaan kuadrat x2 – x + 3 = 0 adalah x1 dan x2. Persamaan kuadrat dengan akar-akar (x1 + 2) dan (x2 + 2)adalah …
A. x2 – x + 9 = 0
B. x2 + 5x + 9 = 0
C. x2 – 5x – 9 = 0
D. x2 – 5x + 5 = 0
E. x2 – 5x + 9 = 0
Jawaban : E
Pembahasan :
PK Baru : x2 – (y1 + y2)x + y1.y2 = 0
y1 + y2 = (x1 + 2) + (x2 + 2)
= (x1 + x2) + 4
= – b/a + 4
= –1/1 + 4
= 5
y1 . y2 = (x1 + 2)(x2 + 2)
= x1.x2 + 2x1 + 2x2 + 4
= x1.x2 + 2(x1 + x2) + 4
= c/a– 2 b/a + 4
= 3/1– 2 -1/1 + 4
= 3 + 2 + 4
= 9
PK Baru : x2 – 3x + 8 = 0
Baca Juga : Soal Fungsi Komposisi dan Invers
27. Sumbu simetri parabola y = x2 – 5x + 3 diperoleh pada garis …
A. x = 3/2
B. x = 3/2
C. x = 5/2
D. x = 5/2
E. x = 3
Jawaban : D
Pembahasan :
Karena sumbu simetri parabola pasti dilewati oleh titik puncak parabola, maka kita bisa peroleh dengan y’ = 0
Y’ = 2x – 5
0 = 2x – 5
x = 5/2
jadi sumbu simetri parabola y = x2 – 5x + 3 adalah x = 5/2
28. Ordinat titik balik maksimum grafik fungsi y = -x2 – (p – 2)x + (p – 4) adalah 6. Absis titik balik maksimum adalah …
A. –4
B. –2
C. – 1/6
D. 1
E. 5
Jawaban : B
Pembahasan :
NOTE : ordinat = sumbu-y, absis = sumbu-x
Karena berbicara titik balik maksimum, maka kita manfaatkan turunan pertama yaitu y’ = 0
-2x – (p – 2) = 0
-2x = p – 2
29. Nilai minimum fungsi f(x) = x2 – 5x + 4 adalah ….
A. –9/4
B. 9/4
C. 5/2
D. -5/2
E. 4
Jawaban : A
Pembahasan :
Perlu dicatat bahwa nilai maksimum atau minimum suatu fungsi pasti berhubungan dengan turunan pertama yaitu f'(x) = 0
2x – 5 = 0
30. Fungsi kuadrat yang grafiknya berpuncak dititik (2, 3) dan melalui titik (-2, 1) adalah …
A. y = -1/8(x – 2)2 + 3
B. y = -1/8(x – 2)2 – 3
C. y = 1/8(x + 2)2 – 3
D. y = 1/8(x + 2)2 + 3
E. y = 1/8(x – 2)2 + 3
Jawaban : A
Pembahasan Soal Persamaan Kuadrat :
f(x) = ax2 + bx + c
f'(x) = 2ax + b
0 = 2a.2 + b
0 = 4a + b
-b = 4a … (i)
nilai fungsi pada titik puncak
f(2) = a(2)2 + b.2 + c
3 = 4a + 2b + c
3 = -b + 2b + c
3 = b + c … (ii)
f(-2) = a(-2)2 + b(-2) + c
1 = 4a – 2b + c
1 = -b – 2b + c
1 = -3b + c … (iii)
eliminasi persamaan (ii) dan (iii)
b + c = 3
-3b + c = 1 –
4b = 2
b = 1/2
substitusi b = 1/2 ke persamaan (ii)
1/2 + c = 3
c = 5/2
substitusi b = 1/2 ke persamaan (i)
-1/2 = 4a
a = -1/8
f(x) = (-1/8)x2 + 1/2 x + 5/2
= (-1/8)x2 + 4/8 x + 5/2
= -1/8(x2 – 4x) + 5/2
= -1/8(x – 2)2 + 4/8 + 5/2
= -1/8(x – 2)2 + 4/8 + 20/8
= -1/8(x – 2)2 + 3
31. Akar-akar persamaan kuadrat 2x² – 13x + 15 = 0 adalah …
A. 3/2 dan 6
B. 3/2 dan 5
C. 1 dan 6
D. 2 dan 3
E. 2 dan 3/2
Jawaban : B
Pembahasan :
32. Jika x1 dan x2 akar-akar persamaan kuadrat x2 + 5x + 6 = 0.
Tentukan nilai :
Jawaban :
Pembahasan :
33. Akar-akar persamaan kuadrat 2x + mx + 16 = 0 adalah α dan β. Jika α =2β dan α, β positif, maka nilai m adalah. . .
Jawaban :
Pembahasan :
2x + mx + 16 = 0 berarti a = 2, b = m, c = 16
Karena α = 2 β maka α nya diganti dengan 2 β sehingga
Dari penjumlahan akar-akar masukkan nilai α dan β yang sudah didapatkan tadi:
34. Jika jumlah kuadrat akar-akar persamaan x2 – 2x + k – 3 = 0 adalah 20 maka tentukan nilai k adalah . . .
Jawaban :
Pembahasan :
x2 – 2x + k – 3 = 0
Dengan nilai a = 1, b = –2, c = k – 3 maka
x1 + x2 = 2
x1 . x2 = k-3
Jumlah kuadrat akar-akarnya
Sudah selesai membaca dan berlatih soal persamaan kuadrat ini ? Ayo lihat dulu Soal Matematika lainnya




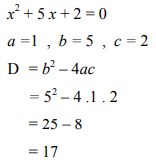
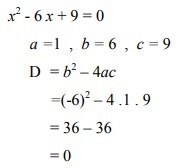

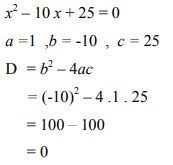
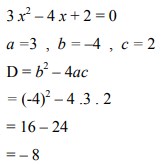

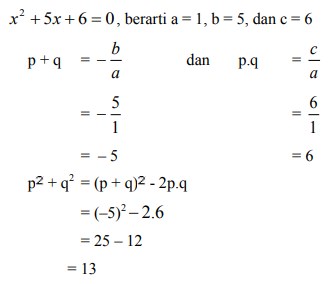
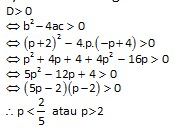
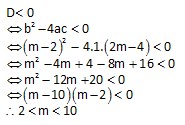
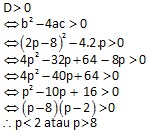
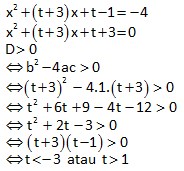
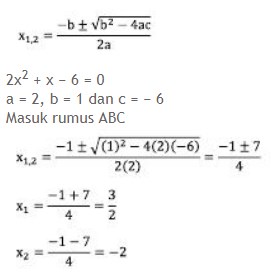
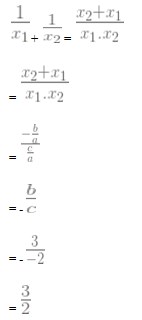

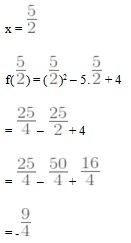
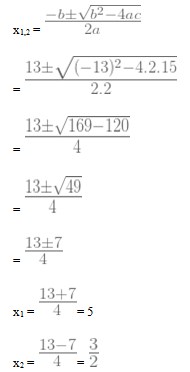
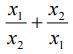
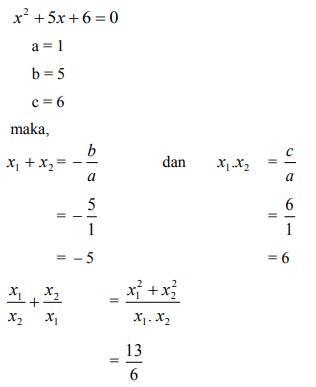
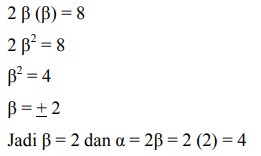
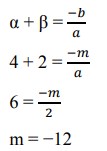
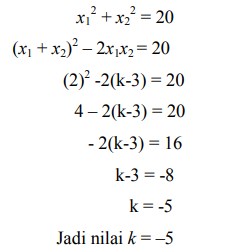



ijin copy pak
Silahkan, semoga bermanfaat
Terimaksih bpk Anas Ilham atas postingan bapak yang dapat menjadi acuan dan contoh bahkan mencopy seluruhnya untuk menjadi bahan ajar pada pada rumah belajar soal dan pembahasan persamaan dan fungsi kuadrat
pak mohon maaf sebelumnya, saya nggak bermaksud menyinggung pihak manapun, dan saya juga tidak bermasuk menjelek jelekan pihak manapun, tetapi saya cuma mau bilang bahwa KIKO ENAK TAU