Contoh Soal Pythagoras dan Jawaban – Teorema Pythagoras merupakan salah satu teorema yang telah dikenal manusia sejak peradapan kuno. Nama teorema ini diambil dari nama seorang matematikawan Yunani yang bernama Pythagoras. Dalam ilmu matematika, Teorema Pythagoras merupakan suatu keterkaitan dalam geometri Euklides antara tiga sisi sebuah segitiga siku-siku. Teorema ini dinamakan menurut nama filsuf Yunani abad ke-6 SM, Pythagoras.

Teorema Pythagoras menyatakan bahwa:
Jumlah luas bujur sangkar pada kaki sebuah segitiga siku-siku sama dengan luas bujur sangkar di hipotenus.
Sebuah segitiga siku-siku adalah segitiga yang mempunyai sebuah sudut siku-siku; kaki-nya adalah dua sisi yang membentuk sudut siku-siku tersebut, dan hipotenus adalah sisi ketiga yang berhadapan dengan sudut siku-siku tersebut.
1 – 10 Contoh Soal (Pythagoras) Pitagoras Beserta Jawaban
1. Berdasarkan teorema Pythagoras, pada segitiga siku-siku, kuadrat panjang sisi miring sama dengan…
a. Selisih kuadrat panjang sisi siku-sikunya
b. Jumlah kuadrat panjang sisi siku-sikunya
c. Selisih akar panjang sisi siku-sikunya
d. Jumlah akar panjang sisi siku-sikunya
Jawaban : B
Pembahasan:
Berdasarkan teorema pythagoras, kuadrat sisi miring sama dengan jumlah kuadrat sisi siku-sikunya. Jadi, jawaban yang tepat B.
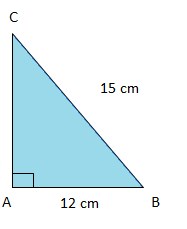
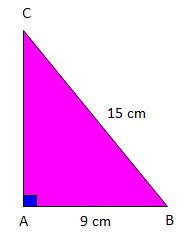
2. Berdasarkan gambar di bawah ini, pernyataan yang benar adalah…
a. AC2 = AB2 + BC2
b. AB2 = AC2 + BC2
c. BC2 = AC2 + AB2
d. AC2 = BC2 + AB2
Jawaban : A
Mari kita cari satu-satu rumus untung mencari masing-masing panjang sisi:
3. Panjang sisi miring pada segitiga siku-siku sama kaki dengan panjang sisi siku-siku p cm adalah… cm.
a. 1/2p
b. p
c. p√2
d. p√3
Jawaban : C
Perhatikan gambar berikut:
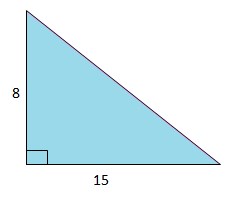
4. perhatikan gambar berikut!
Panjang sisi miring adalah…
a. 16 cm
b. 17 cm
c. 18 cm
d. 19 cm
Jawaban : B
Pembahasan:
5. Perhatikan gambar berikut!
Panjang AC adalah…
a. 3 cm
b. 6 cm
c. 9 cm
d. 10 cm
Jawaban : C
Baca Juga : Soal Persamaan Trigonometri
6. Dari tiga bilangan berikut, yang merupakan tripel pythagoras adalah…
a. 9, 13, 15
b. 7, 12, 15
c. 10, 24, 25
d. 8, 15, 17
Jawaban : D
Mari kita bahas masing-masing opsi di atas:
7. Berikut ini adalah ukuran sisi-sisi dari empat buah segitiga, yaitu:
I. 3 cm, 4, cm, 5 cm
II. 7 cm, 8 cm, 9 cm
III. 5 cm, 12 cm, 15 cm
IV. 7 cm, 24 cm, 25 cm
Yang merupakan ukuran segitiga siku-siku adalah…
a. I dan II
b. I dan III
c. II dan III
d. I dan IV
Jawaban : D
Pembahasan :
Mari kita bahas masing-masing opsi di atas:
I. 3 cm, 4, cm, 5 cm
52 = 42 + 32
25 = 16 + 9
25 = 25 (sama, segitiga siku-siku)
II. 7 cm, 8 cm, 9 cm
152 = 122 + 52
81 = 64 + 49
81 = 113 (81 < 113, ini menandakan segitiga lancip)
III. 5 cm, 12 cm, 15 cm
152 = 122 + 52
225 = 144 + 25
225 = 169 (225 > 169, ini menandakan segitiga tumpul)
IV. 7 cm, 24 cm, 25 cm
252 = 122 + 52
625 = 576 + 49
625 = 625 (sama, ini menandakan segitiga siku-siku)
Jawaban yang tepat D.
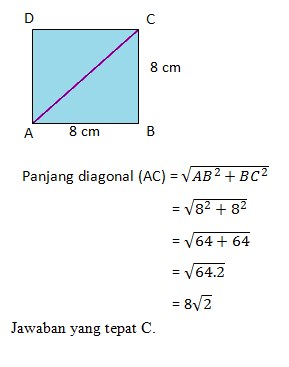
8. Sebuah persegi mempunyai panjang sisi 8 cm. Panjang diagonal persegi tersebut adalah…
a. 4√2
b. 4√3
c. 8√2
d. 8√3
Jawaban : C
Perhatikan gambar persegi berikut ini:
9. Sebuah persegi panjang memiliki panjang 16 cm dan lebar 12 cm. Panjang diagonal persegi panjang tersebut adalah…
a. 24 cm
b. 22 cm
c. 20 cm
d. 18 cm
Jawaban : C
Pembahasan:
Perhatikan gambar berikut:
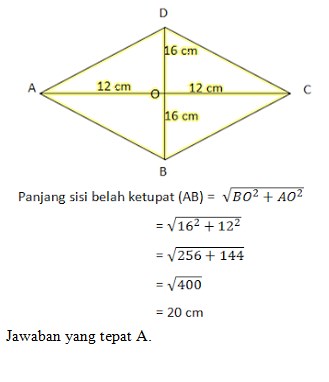
10. Sebuah bangun berbentuk belah ketupat mempunyai panjang diagonal 24 cm dan 32 cm. Panjang sisi belah ketupat tersebut adalah…
a. 20 cm
b. 28 cm
c. 40 cm
d. 56 cm
Jawaban : A
Perhatikan gambar belah ketupat berikut:
11 – 20 Contoh Soal Pythagoras Pilihan Ganda dan Jawaban
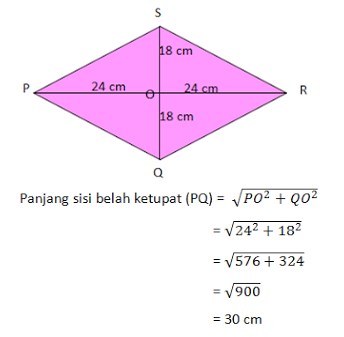
11. Panjang diagonal-diagonal suatu belah ketupat 36 cm dan 48 cm. Panjang sisi belah ketupat tersebut adalah…
A. 20 cm
B. 30 cm
C. 40 cm
D. 50 cm
Jawaban : B
Pembahasan :
Perhatikan gambar belah ketupat berikut:
Jawaban yang tepat B.
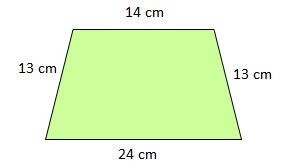
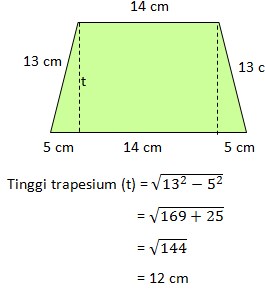
12. Perhatikan gambar trapesium sama kaki berikut!
Tinggi trapesium tersebut adalah…
A. 12 cm
B. 11 cm
C. 10 cm
D. 9 cm
Jawaban : A
Pembahasan :
Perhatikan gambar trapesium berikut:
Jawaban yang tepat A.
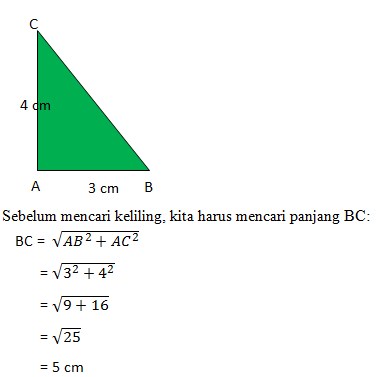
13. Sebuah segitiga siku-siku memiliki panjang sisi siku-siku 3 cm dan 4 cm. Keliling segitiga tersebut adalah…
A. 15 cm
B. 14 cm
C. 13 cm
D. 12 cm
Jawaban : D
Pembahasan :
Perhatikan segitiga siku-siku di bawah ini:
Keliling segitiga ABC = AB + BC + AC
= 3 + 5 + 4
= 12 cm
Jawaban yang tepat D.
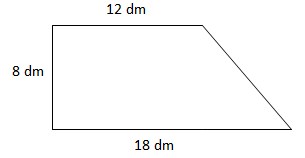
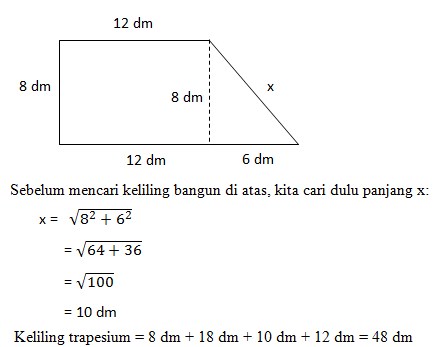
14. Perhatikan trapesium berikut!
Keliling trapesium di atas adalah…
A. 46 dm
B. 48 dm
C. 50 dm
D. 52 dm
Jawaban : B
Pembahasan :
Jawaban yang tepat B.
15. Perhatikan gambar berikut!
Luas segitiga ABC adalah…
A. 45 cm2
B. 54 cm2
C. 108 cm2
D. 135 cm2
Jawaban : B
Pembahasan :
Sebelum mencari luas, kita harus mencari tinggi (AC):
Luas segitiga ABC
= ½ x alas x tinggi
= ½ x AB x AC
= ½ x 9 x 12
= 54 cm2
Jawaban yang tepat B
Baca Juga : Soal Notasi Sigma
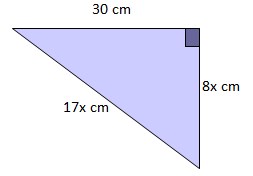
16. Perhatikan gambar berikut!
Luas segitiga di atas adalah…
A. 60 cm2
B. 120 cm2
C. 240 cm2
D. 480 cm2
Jawaban : C
Pembahasan :
Sebelum mencari luas, kita cari dulu x dan panjang alasnya:
panjang alas segitiga = 8x = 8 • 2 = 16 cm
Luas segitiga
= ½ x alas x tinggi
= ½ x 16 x 30
= 240 cm²
Jawaban yang tepat C
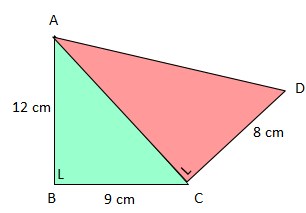
17. Perhatikan gambar!
Panjang AD adalah…
A. 15 cm
B. 17 cm
C. 24 cm
D. 25 cm
Jawaban : B
Pembahasan :
Sebelum mencari panjang AD, kita cari dulu panjang AC:
Jawaban yang tepat B.
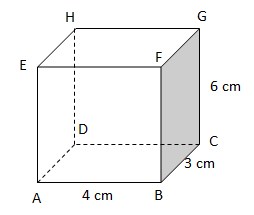
18. Perhatikan gambar berikut!
Luas bidang diagonal ACGE adalah…
A. 12 cm2
B. 24 cm2
C. 30 cm2
D. 72 cm2
Jawaban : C
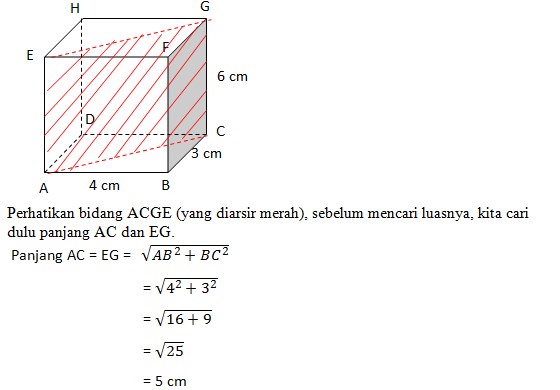
Pembahasan :
Perhatikan gambar berikut:
Luas ACGE
= panjang x lebar
= AC x CG
= 5 x 6
= 30 cm2
Jawaban yang tepat C.
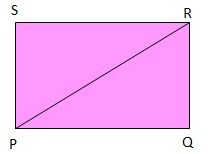
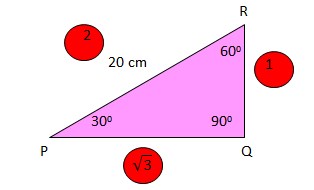
19. Pada persegi panjang PQRS, panjang PR = 20 cm dan besar <QPR = 30 derajat. Luas persegi panjang PQRS adalah…
A. 100√3
B. 100√2
C. 200√3
D. 200√2
Jawaban : A
Pembahasan :
Perhatikan gambar segitiga PQR berikut ini:
Perhatikan angka-angka dalam bulatan merah. Angka ini didapatkan karena sudut 30 derajat
Jadi, luas persegi panjang
= panjang x lebar
= PQ x QR
= 10 √3 x 10
= 100√3
Jawaban yang tepat A.
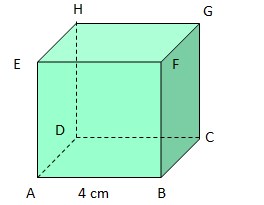
20. Perhatikan gambar kubus berikut!
Panjang diagonal ruang EC adalah…
A. 4 cm
B. 4√2 cm
C. 4√3 cm
D. 4√6 cm
Jawaban : C
Pembahasan :
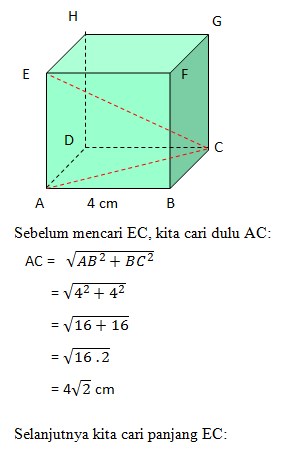
Perhatikan gambar di bawah ini:
Jawaban yang tepat C.
Sudah selesai membaca dan berlatih Soal Pythagoras ini ? Ayo lihat dulu Soal Matematika lainnya
Ulasan Akhir Soal Pythagoras
Apakah kalian tahu apakah kegunaan dari kita mempelajari teorema pythagoras? Suatu ilmu akan lebih terasa menarik bila ada keterkaitan dengan kegiatan dan kebermanfaatan dalam kehidupan sehari-hari . Misal, seorang pekerja bangunan sedang memeriksa kesikuan sebelum membuat desain pondasi suatu bangunan. Dalam memeriksa kesikuan ini mereka menggunakan Tripel Pythagoras, meski secara ilmiah Pak Tukang tidak mengerti alasan mengapa menggunakan itu. Nah, inilah salah satu penerapan Teorema Pythagoras dalam kehiduapan sehari-hari.
Terdapat beberapa cara dalam membuktikan teorema, yaitu dengan pendekatan luas persegi, luas segitiga sama sisi, luas trapesium, dan luas bentuk bangun datar lainnya. Salah satu pembuktikan teorema adalah pembuktian yang diemukan oleh James A. Garfield, Presiden ke-20 Amerika Serikat. Beliau membuktikan teorema ini dengan menggunakan luas teorema pytagoras.


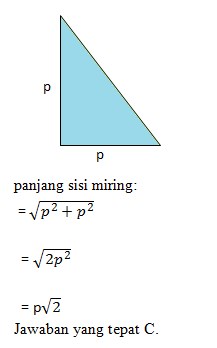
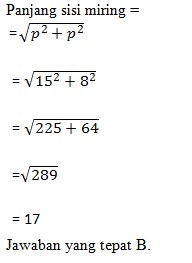



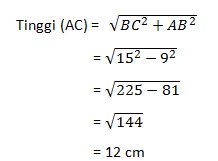
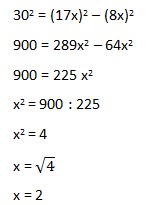





Terimakasih..
Saya merasa sangat terbantu terima kasih..