Contoh Soal Transformasi Geometri (Translasi, Refleksi, Rotasi, Dilatasi) dan Jawaban – Transformasi geometri adalah salah satu studi matematika berkaitan dengan perubahan suatu bidang geometri yang meliputi posisi, besar dan bentuknya.

Transformasi geometri atau sering disebut geometri adalah mengubah setiap koordinat titik (titik-titik dari suatu bangun) menjadi koordinat lainnya pada bidang dengan suatu aturan tertentu. Misalnya, transformasi T terhadap titik P (x,y) menghasilkan bayangan P’ (‘,y’)
Transformasi merupakan suatu pemetaan titik pada suatu bidang ke himpunan titik pada bidang yang sama. Jenis-jenis dari transformasi yang dapat dilakukan antara lain :
Translasi (Pergeseran) adalah pemindahan atau pergeseran suatu objek sepanjang garis lurus dengan arah dan jarak tertentu
Refleksi (Pencerminan) adalah transformasi yang memindahkan setiap titi pada bidang dengan sifat pencerminan.
Rotasi (Perputaran) adalah transformasi dengan cara memutar objek dengan titik pusat tertentu.
Dilatasi (Penskalaan)

1 – 10 Soal Transformasi Geometri dan Jawaban
1. Bayangan garis y = 2x + 2 yang dicerminkan terhadap garis y= x adalah. . .
Jawaban : C
Pembahasan :
2. Persamaan bayangan kurva y = x² – 2x – 3 oleh rotasi [0, 180°], kemudian dilanjutkan oleh pencerminan terhadap garis y = -x adalah ….
A. y = x² – 2x – 3
B. y = x² – 2x + 3
C. y = x² + 2x + 3
D. x = y² – 2y – 3
E. x = y² + 2y + 3
Jawaban : D
Pembahasan :
Rotasi sudut-sudut yang lain dapat dihitung sendiri menggunakan kaidah trigonometri.
pencerminan terhadap garis y = -x
3. Persamaan bayangan dari lingkaran x² +y² +4x – 6y – 3 = 0 oleh transformasi yang berkaitan dengan matriks adalah….
A. x² + y² – 6x – 4y- 3 = 0
B. X² + y² – 6x + 4y- 3 = 0
C. x² + y² + 6x – 4y- 3 = 0
D. x² + y² – 4x + 6y- 3 = 0
E. x² + y² + 4x – 6y+ 3 = 0
Jawaban : A
Pembahasan :
4. T1 dan T2 adalah transformasi yang masing-masing bersesuaian dengan 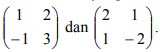
Jawaban : E
Pembahasan :
5. Ditentukan matriks transformasi .
Hasil transformasi titik (2,-1) terhadap T1 dilanjutkan T2 adalah….
A. (-4,3)
B. (-3,4)
C. (3,4)
D. (4,3)
E. (3,-4)
Jawaban : A
Pembahasan :
Baca Juga : Soal Sistem Persamaan Linear Tiga Variabel (SPLTV)
6. Persamaan bayangan garis y = -6x + 3 karena transformasi oleh matriks kemudian dilanjutkan dengan matriks
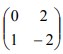
A. x + 2y + 3 = 0
B. x + 2y – 3 = 0
C. 8x – 19y + 3 = 0
D. 13x + 11y + 9 = 0
E. 13x + 11y – 9 = 0
Jawaban : E
Pembahasan :
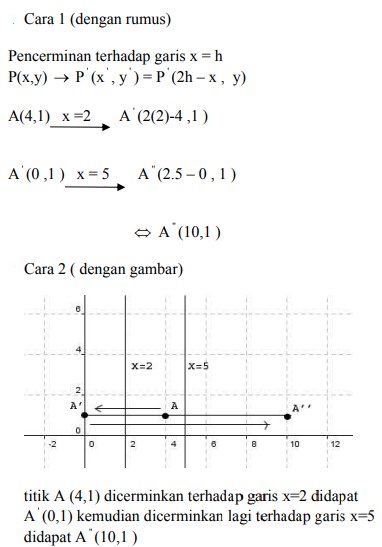
7. Bayangan titik A (4,1) oleh pencerminan terhadap garis x =2 dilanjutkan pencerminan terhadap garis x = 5 adalah titik….
A. A” (8,5)
B. A” (10,1)
C. A” (8,1)
D. A” (4,5)
E. A” (20,2)
Jawaban : B
Pembahasan :
8. T1 adalah transformasi yang bersesuaian dengan matriks 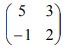
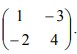
A. 4
B. 5
C. 6
D. 7
E. 8
Jawaban : B
Pembahasan :
9. Bayangan ∆ABC dengan A(2,1), B(6,1), C(5,3) karena refleksi terhadap sumbu y dilanjutkan rotasi (0,90°) adalah…
A. A” (-1,-2), B” (1,6) dan C” (-3,-5)
B. A” (-1,-2), B” (1,-6) dan C” (-3,-5)
C. A” (1,-2), B” (-1,6) dan C” (-3,5)
D. A” (-1,-2), B” (-1,-6) dan C” (-3,-5)
E. A” (-1,2), B” (-1,-6) dan C” (-3,-5)
Jawaban : D
Pembahasan :
10. Persamaan peta kurva y = x² – 3x + 2 karena pencerminan terhadap sumbu x dilanjutkan dilatasai dengan pusat O dan factor skala 3 adalah…
A. 3y + x² – 9x + 18 = 0
B. 3y – x² + 9x – 18 = 0
C. 3y – x² + 9x + 18 = 0
D. 3y + x² + 9x + 18 = 0
E. y + x² + 9x – 18 = 0
Jawaban : A
Pembahasan :
pencerminan terhadap sumbu x:
P ( x , y ) → P ‘ ( x , – y )
Dilatasi terhadap titik pusat O(0,0) dengan factor skala 3 :
[O, k] : P(x,y) → P'(kx, ky)
[O,3k] : P(x,y) → P'(3x, 3y)
pencerminan terhadap sumbu x dilanjutkan dilatasai dengan pusat O dan factor skala 3 :
P(x,y) → P ‘(x, -y) → P ”(3x, -3y)
11 – 20 Soal Transformasi Geometri dan Jawaban
11. Luas bayangan persegipanjang PQRS dengan
P(-1,2), Q(3,2), R (3,-1), S(-1,-1)
karena dilatasi [0,3] dilanjutkan rotasi pusat O bersudut π/2 adalah…
A. 36
B. 48
C.72
D. 96
E. 108
Jawaban : E
Pembahasan :
dilatasi [0,3] :
[O,3k] : P(x,y) → P ‘(3x, 3y)
Sehingga :
P(x,y) → P” (-3y, 3x)
P(-1,2), Q(3,2), R (3,-1), S(-1,-1)
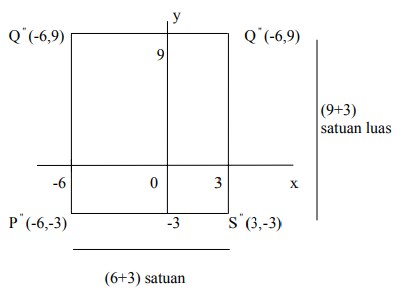
P(-1,2) → P” (-6,-3)
Q(3,2) → Q” (-6,9)
R (3,-1) → R” (3,9)
S(-1,-1) → S” (3,-3)
Buat sketsa gambarnya:
Sehingga luas transformasinya adalah :
Panjang (p) x lebar (l) = 12 x 9 = 108 satuan luas
12. Segitiga ABC dengan A(2,1), B(6,1), C(6,4) ditransformasikan dengan matriks transformasi 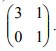
A. 56 satuan luas
B. 36 satuan luas
C. 28 satuan luas
D. 24 satuan luas
E. 18 satuan luas
Jawaban : E
Pembahasan :
misalkan T =
maka
Luas bayangan/transformasi ∆ ABC =|det T| x luas ∆ ABC |det T| = |ad –bc| = |3-0| = 3
luas ∆ ABC :
buat sketsa gambar :
Luas bayangan/transformasi ∆ ABC =|det T| x luas ∆ ABC
= 3 x 6 = 18 satuan luas
13. Tentukan bayangan lingkaran (x-3)2 + (y+1)2 = 4 jika ditranslasikan
a. 5
b. 4
c. 3
d. 2
e. 1
Jawaban : B
Pembahasan :
Ambil sembarang titik P(a,b) pada lingkaran (x-3)2 + (y+1)2 = 4 sehingga diperoleh (a-3)2 + (b+1)2 = 4
14. ABCD adalah sebuah persegi dengan koordinat titik-titik sudut A(1,1), B(2,1), C(2,2) dan D(1,2). Tentukan peta atau bayangan dari titik-titik sudut persegi itu oleh dilatasi [O,2]!
Jawaban :
Pembahasan :
15. Jika titik A(15,8) dicerminkan terhadap garis x=7, maka bayangan titik A adalah titik A’ dengan koordinat….
Jawaban :
Pembahasan :
Baca Juga : Soal Sistem Persamaan Linear Dua Variabel (SPLDV)
16. Titik A(a,b) dicerminkan terhadap garis x=2 menghasilkan bayangan titik A’(0,2), maka nilai (a,b) berturut-turut adalah….
a. 2 , 4
b. 4 , 2
c. 2 , 2
d. 3 , 1
e. 1 , 3
Jawaban : B
Pembahasan :
17. Titik A’(-16,24) merupakan bayangan dari titik A(x,y) yang didilatasikan dengan pusat O(0,0) dan faktor skala -4. Koordinat titik A adalah….
Jawaban :
Pembahasan :
18. Tentukan persamaan peta dari garis 3x – 5y + 15 = 0 oleh pencerminan terhadap sumbu x!
Jawaban :
Pembahasan :
19. Tentukan persamaan peta dari garis 3x-5y+15=0 oleh dilatasi terhadap pusat O(0,0) dengan faktor skala 5!
Jawaban :
Pembahasan :
20. Lingkaran x² + y² – 6x + 2y + 1 = 0. Jika ditransformasikan dengan dilatasi [O,4], persamaan bayangannya adalah….
Jawaban :
Pembahasan :
21 – 30 Soal Transformasi Geometri dan Jawaban
21. Tentukan bayangan titik A(3,-7) oleh translasi (4, 2) adalah. . .
Pembahasan :
22. Tentukan bayangan titik P(-1,3) oleh translasi T (3, -1) adalah. . .
Pembahasan :
23. Diketahui titik A (7,-2) ditranslasikan berturut-turut oleh (-3,1) kemudian ditranslasikan kembali (3,2) Tentukanlah bayangan titik P adalah. . .
Pembahasan :
24. Titik P(-3,7) dicerminkan terhadap garis y = -x. Tentukanlah koordinat bayangan titik P adalah. . .
Pembahasan :
25. Titik A (3, 2) dicerminkan terhadap x=2, tentukan bayangan dari titik A adalah. . .
Pembahasan :
Simak Juga : Soal Fungsi Komposisi
26. Titik Q(1, -3) dirotasikan dengan pusat di O(0,0) sebesar 270°, maka bayangan koordinat titik B tersebut adalah . . .
Pembahasan :
27. Diketahui segitiga PQR dengan titik P(2,-2), Q(2,1), dan R(4,1). segitiga tersebut dirotasikan 180° terhadap titik pusat O(0,0). Tentukan bayangan segitiga PQR adalah. . .
Pembahasan :
28. Diketahui segitiga ABC dengan A (2, -2), B(-2, 5) dan C(4, -2). Dilatasi dititik pusat O(0,0) dengan skala 2. Tentukan bayangan hasil dilatasi pada segitiga ABC adalah. . .
Pembahasan :
29. Diketahui titik B(5, 2) dilatasikan pada titik pusat (-3, 4) dengan faktor skala -2. Tentukan hasil dilatasi pada titik B tersebut adalah. . .
Pembahasan :
30. Tentukan bayangan titik P(-3,4), Q(4,4) dan R(4,7) dilatasi oleh translasi T = (-3,4) adalah. . .
Pembahasan :
Sudah selesai membaca dan berlatih soal ini ? Ayo lihat dulu Soal Matematika lainnya

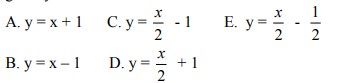

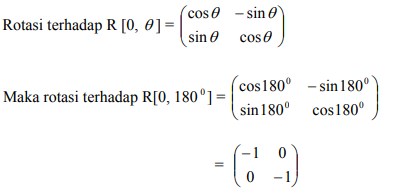


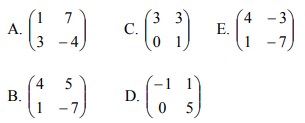

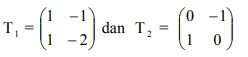


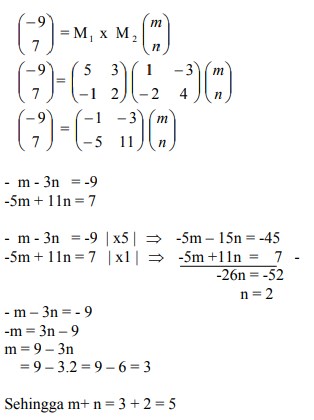


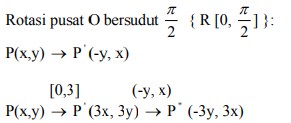
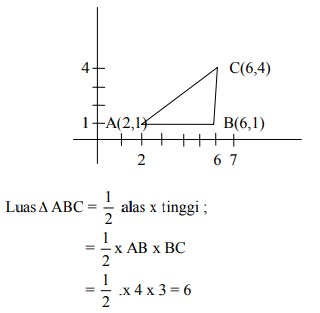
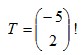







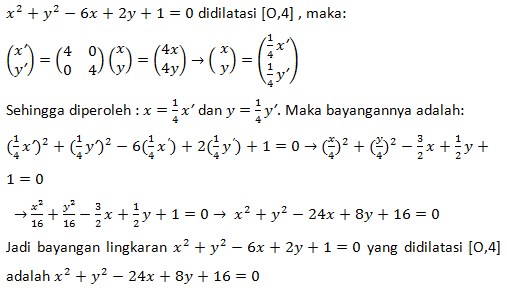













bagus soalnya pas banget butuh soal ini