Soal Ujian Matematika Kelas 10 Semester 1 Pilihan Ganda Kurikulum 2013 beserta Jawabannya – Kali ini tim soalkimia.com akan membagikan 30 butir soal untuk siswa pelajari sebelum menghadapi ujian MTK semester satu.

Pada kelas 1 semester ganjil siswa mempelajari materi :
- Bentuk Pangkar, Akar, dan Logaritma
- Persamaan Linear
- Nilai Mutlak
- SPLDV
- Program Linear
- Barisan dan Deret
1 – 10 Soal Ujian Matematika Semester 1 Pilihan Ganda dan Kunci Jawaban
1. Sederhanakan :
5√24 + 3√3(√18 + 2√32)
A. 40√6
B. 41√6
C. 42√6
D. 43√6
E. 44√6
Jawaban : D
Pembahasan :
5√24 + 3√3(√18 + 2√32)
= 5√4 √6 + 3√3 √18 + 3√3 . 2√32
=5.2 √6 + 3√3 √9√2 + 3√3 .2√16√2
= 10√6 + 3√3 .3√2 + 3√3 . 2 .4√2
= 10√6 + 9√6 + 24√6 = 43√6
2. Sederhanakan:
(1 + 3√2) − (4 − √50)
A. 8√2 – 3
B. 2√2 − 3
C. 8√2 + 3
D. 2√2 + 3
E. 4√2 − 3
Jawaban : C
Pembahasan :
(1 + 3√2) − (4 − √50)
= 1 + 3√2 − 4 + √50
= 1 + 3√2 − 4 + √25 √2
= 1 + 3√2 − 4 + 5√2
= − 3 + 8√2 atau = 8√2 − 3
3. Tentukanlah Bentuk sederhana dari adalah….
Jawaban : A
Pembahasan :
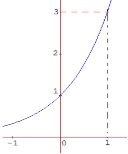
4. Fungsi eksponensial dari grafik di bawah ini adalah ….
A. f(x)=32x
B. f(x)=3x
C. f(x)=3-x
D. f(x)=2x
E. f(x)=2-x
Jawaban: B
Pembahasan
Pada grafik di atas dapat dilihat melalui dua titik, yaitu (0,1) dan (1,3). Untuk mendapatkan fungsi eksponensial tersebut, kita harus mensubstitusikan kedua titik yang ada ke dalam persamaan fungsi eksponensial secara umum f(x)=b × ax untuk mencari nilai a dan b, sehingga:
Untuk titik (0,1) didapat f(x)=b × ax
1 = b × a0
1 = b × 1
b = 1
Untuk titik (1,3) didapat f(x)=b × ax=1 × ax=ax (masukkan nilai b = 1)
f(x) = ax
3 = a1
3 = a
Maka, fungsi eksponensial dari grafik tersebut adalah
f(x) = b × ax
f(x) =1 × 3x
f(x) =3x
5. Tentukan nilai dari: 2log 8 + 3log 9 + 5log 125 adalah…
A. -4
B. -8
C. 0
D. 4
E. 8
Jawaban : E
Pembahasan :
2log 8 + 3log 9 + 5log 125
= 2log 23 + 3log 32 + 5log 53 = 3 2log 2 + 2 3log 3 + 3 5log 5
= 3 + 2 + 3 = 8
Baca Juga : 20+ Soal Pangkat, Akar, dan Logaritma Pilihan Ganda [+Pembahasan]
6. Tentukan nilai dari 2log 1/8 + 3log 1/9 + 5log 1/125 adalah…
A. -4
B. -8
C. 0
D. 4
E. 8
Jawaban : B
Pembahasan :
2log 1/8 + 3log 1/9 + 5log 1/125
= 2log 2−3 + 3log 3−2 + 5log 5−3
= − 3 − 2 − 3 = − 8
7. Tentukan nilai dari 4log 8 + 27log 9 adalah. . .
A. 10/6
B. 12/6
C. 13/6
D. 14/6
E. 15/6
Jawaban : C
Pembahasan :
4log 8 + 27log 9
= 22log 23 + 33log 32
= 3/2 2log 2 + 2/3 3log 3
= 3/2 + 2/3 = 9/6 + 4/6 = 13/6
8. Tentukan nilai dari 8log 4 + 27log 1/9 adalah. . .
A. -2
B. -1
C. 0
D. 1
E. 2
Jawaban : C
Pembahasan :
8log 4 + 27log 1/9
23log 22 + 33log 3−2
= 2/3 2log 2 + (−2/3) 3log 3
= 2/3 − 2/3 = 0
9. Tentukan nilai dari √2log 8 adalah. . .
A. 10
B. 8
C. 6
D. 4
E. 2
Jawaban : C
Pembahasan :
√2log 8
= 21/2log 23 = 3/0,5 2log 2 = 3/0,5 = 6
10. Tentukan nilai dari √3log 27 adalah. . .
A. 10
B. 8
C. 6
D. 4
E. 2
Jawaban : D
Pembahasan :
√3log 9
= 31/2log 32 = 2/0,5 3log 3 = 2/0,5 = 4
11 – 20 Soal Ujian Matematika K13 Semester 1 beserta Pembahasannya
11. Diketahui:
log p = A
log q = B
Tentukan nilai dari log p3 q2
A. 2A + 2B
B. 2A + 3B
C. 3A + 3B
D. A + B
E. 3A + 2B
Jawaban : E
Pembahasan :
log p3 q2 = log p3 + log q2 = 3 log p + 2 log q = 3A + 2B
11. Nilai x dari persamaan linier 7x+23=4x-1 adalah ….
A. -3
B. -1
C. 0
D. 1
E. 3
Jawaban: D
Pembahasan
7x + 23 = 4x – 1
7x + 2 = 3 ( 4x – 1)
7x + 2 = 12x – 3
7x – 12x = – 3 – 2
– 5 x = -5
12. Diberikan dua buah persamaan yaitu persamaan linear dua variable dan kuadrat sebagai berikut:
- (i) y = 2x + 3
- (ii) y = x2 − 4x + 8
Tentukan himpunan penyelesaian (Hp) dari kedua persamaan tersebut!
A. {(10, 5), (5, 13)}
B. {(1, 5), (2, 13)}
C. {(2, 5), (5, 13)}
D. {(10, 5), (2, 13)}
E. {(1, 5), (5, 13)}
Jawaban : E
Pembahasan :
Substitusikan y dari persamaan (i) ke y pada persamaan (ii), atau sebaliknya dari (ii) ke (i), lanjutkan dengan operasi aljabar.
x2 − 4x + 8 = 2x + 3
x2 − 4x + 8 − 2x − 3 = 0
x2 − 6x + 5 = 0
Berikutnya faktorkan:
x2 − 6x + 5 = 0
(x − 1)(x − 5) = 0
Dapatkan nilai x yang pertama:
x − 1 = 0
x = 1
Dapatkan nilai x yang kedua:
x − 5 = 0
x = 5
Berikutnya mencari nilai-nilai dari y dengan substitusi nilai x ke persamaan (i):
Untuk
x = 1 maka
y = 2x + 3
y = 2(1) + 3
y = 2 + 3
y = 5
Dari sini didapatkan pasangan (x, y) yaitu (1, 5)
Untuk x = 5 maka
y = 2x + 3
y = 2(5) + 3
y = 10 + 3
y = 13
Dari sini didapatkan pasangan (x, y) yaitu (5, 13)
Sehingga himpunan penyelesaiannya :{(1, 5), (5, 13)}
14. Diberikan dua buah persamaan sebagai berikut:
- (i) y = 5x + 4
- (ii) y = x2 + 13x − 16
Tentukan himpunan penyelesaian (Hp) dari kedua persamaan tersebut!
A. {(− 10, − 46), (2, 14)}
B. {(− 10, − 46), (2, 12)}
C. {(− 10, − 45), (2, 14)}
D. {(− 5, − 46), (2, 14)}
E. {(− 10, − 45), (2, 12)}
Jawaban : A
Pembahasan :
x2 + 13x − 16 = 5x + 4
x2 + 13x − 16 − 5x − 4 = 0
x2 + 8x − 20 = 0
(x + 10)(x − 2) = 0
Nilai x yang pertama
x + 10 = 0
x = − 10
Nilai x yang kedua
x − 2 = 0
x = 2
Nilai-nilai y, dari persamaan pertama:
Untuk x = − 10 didapat nilai y
y = 5x + 4
y = 5(−10) + 4 = − 46
Untuk x = 2, didapat nilai y
y = 5x + 4
y = 5(2) + 4 = 14
Hp : {(− 10, − 46), (2, 14)}
14. Diketahui log 40 = A dan log 2 = B, tentukan nilai dari log 20
A. 2A − B
B. 2A + B
C. A − 2B
D. A + B
E. A − B
Jawaban : E
Pembahasan
log 20 = log 40/2 = log 40 − log 2 = A − B
15. Diketahui 2log √ (12 x + 4) = 3. Tentukan nilai x
A. 1
B. 2
C. 3
D. 4
E. 5
Jawaban : E
Pembahasan
2log √ (12 x + 4) = 3
Ruas kiri bentuknya log, ruas kanan belum bentuk log, ubah dulu ruas kanan agar jadi bentuk log. Ingat 3 itu sama juga dengan 2log 23 . Ingat rumus alog ab = b jadi
2log √( 12 x + 4) = 2log 23
Kiri kanan sudah bentuk log dengan basis yang sama-sama dua, hingga tinggal menyamakan yang di dalam log kiri-kanan atau coret aja lognya:
2log √( 12 x + 4) = 2log 23
√( 12 x + 4) = 23
√( 12 x + 4) = 8
Agar hilang akarnya, kuadratkan kiri, kuadratkan kanan. Yang kiri jadi hilang akarnya:
12 x + 4 = 82
12x + 4 = 64
12 x = 60
x = 60/12 = 5
Lihat Juga : 20+ Contoh Soal Program Linear Pilihan Ganda [+Pembahasan]
16. Tentukan nilai dari 3log 5log 125 adalah . . .
A. 1
B. 2
C. 3
D. 4
E. 5
Jawaban : A
Pembahasan
3log 5log 125 = 3log 5log 53
= 3log 3 = 1
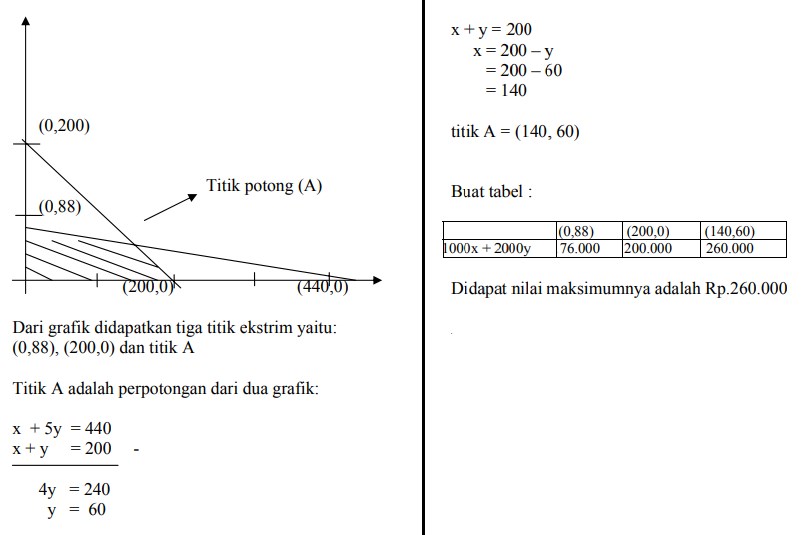
17. Luas daerah parkir 1.760 m² . Luas rata-rata untuk mobil kecil 4 m² dan mobil besar 20 m² . Daya tampung maksimum hanya 200 kendaraan, biaya parker mobil kecil Rp. 1000/jam dan mobil besar Rp.2000/jam. Jika dalam satu jam terisi penuh dan tidak ada kendaraan yang pergi dan dating, maka hasil maksimum tempat parkir itu adalah:
A. Rp.176.000,-
B. Rp. 200.000,-
C. Rp.260.000,-
D. Rp. 300.000,-
E. Rp.340.000,-
Jawaban : C
Pembahasan :
Dibuat persamaan-persamaannya terlebih dahulu:
Misal mobil kecil = x dan mobil besar = y
4 x + 20 y ≤ 1760
x + 5y ≤ 440 …..(1)
x + y ≤ 200 ….(2)
nilai maksimum 1000x + 2000y = ?
buat sketsa grafiknya:
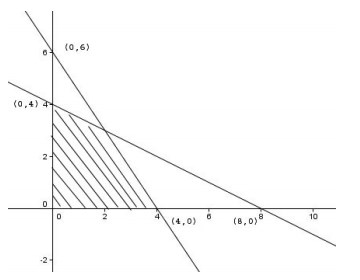
18. Daerah yang diarsir merupakan himpunan penyelesaian dari sistem pertidaksamaan linear…
A. x + 2y ≤ 8, 3x + 2y ≤ 12, x ≥ 0, y ≥ 0
B. x + 2y ≥ 8, 3x + 2y ≥ 12, x ≥ 0, y ≥ 0
C. x – 2y ≥ 8, 3x – 2y ≤ 12, x ≥ 0, y ≥ 0
D. x + 2y ≤ 8, 3x – 2y ≥ 12, x ≥ 0, y ≥ 0
E. x + 2y ≤ 8, 3x + 2y ≥ 12, x ≥ 0, y ≥ 0
Jawaban : A
Pembahasan :
karena daerah arsiran dibawah persamaan garis maka
x + 2y ≤ 8 ….(2)
Arsiran di atas sumbu x dan di kanan sumbu y maka x ≥ 0 dan y≥ 0 ….(3) dan (4)
sehingga daerah penyelesaiannya adalah:
(1), (2), (3) dan (4)
3x + 2y ≤ 12, x + 2y ≤ 8 dan x≥ 0, y≥ 0
Jawaban : A
19. Daerah yang diarsir pada gambar di bawah adalah himpunan penyelesaian dari sistem pertidaksamaan…
A. 5x + 3y ≤ 30, x – 2y ≥ 4, x ≥ 0, y ≥ 0
B. 5x + 3y ≤ 30, x – 2y ≤ 4, x ≥ 0, y ≥ 0
C. 3x + 5y ≤ 30, 2x – y ≥ 4, x ≥ 0, y ≥ 0
D. 3x + 5y ≤ 30, 2x – y ≤ 4, x ≥ 0, y ≥ 0
E. 3x + 5y ≥ 30, 2x – y ≤ 4, x ≥ 0, y ≥ 0
Jawaban : D
Pembahasan :
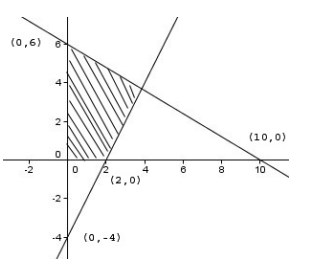
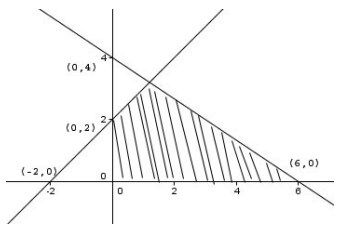
20. Daerah yang diarsir pda gambar di bawah ini menunjukkan himpunan titik (x,y) yang memenuhi pembatasan di bawah ini, yaitu ….
A. x ≥ 0, y ≥ 0, 2x + 3y ≤ 12, – x + y ≥ 2
B. x ≥ 0, y ≥ 0, 2x + 3y ≥ 12, -x + y ≥ 2
C. x ≥ 0, y ≥ 0, 2x + 3y ≤ 12, -x + y ≤ 2
D. x ≥ 0, y ≥ 0, 2x + 3y ≥ 12, -x + y ≤ 2
E. x ≥ 0, y ≥ 0, 2x + 3y ≤ 12, -x + y ≤ 2
Jawaban : C
Pembahasan :
21 – 30 Soal Ujian Matematika K13 Semester 1 beserta Pembahasannya
21. Nilai 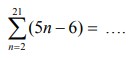
A. 882
B. 1030
C. 1040
D. 1957
E. 2060
Jawaban : B
Pembahasan :
22. Diketahui 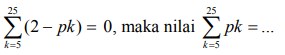
A. 21
B. 28
C. 30
D. 42
E. 112
Jawaban : A
Pembahasan :
23. Suku keempat dan suku ketujuh barisan aritmetika berturut-turut adalah 17 dan 29. Suku ke 25 barisan tersebut adalah….
A. 97
B. 101
C. 105
D.109
E. 113
Jawaban : B
Pembahasan :
24. Suatu deret aritmetika, diketahui jumlah 5 suku yang pertama = 35 dan jumlah 4 suku yang pertama = 24, suku yang ke 15 = ….
A. 11
B. 25
C. 31
D. 33
E. 59
Jawaban : C
Pembahasan :
25. Dari suatu barisan aritmetika, suku ketiga adalah 36, jumlah suku kelima dan ketujuh adalah 144. Jumlah 10 suku pertama deret tersebut adalah…
A. 840
B. 660
C. 640
D. 630
E. 315
Jawaban : B
Pembahasan :
Simak juga : 25+ Contoh Soal Statistika Pilihan Ganda dan Jawaban [+Pembahasan]
Download Soal mtk kelas 10 semester 1 ini disini

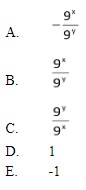
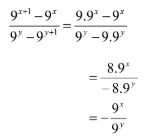



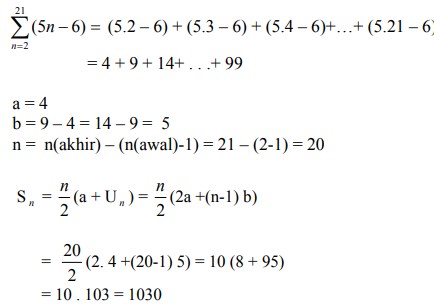

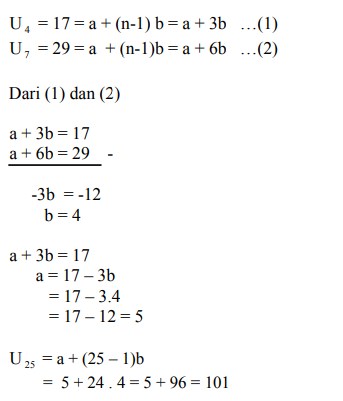
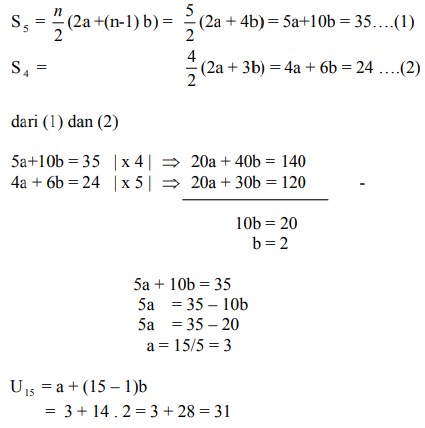
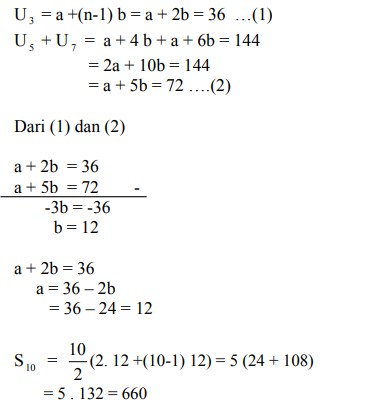



OK