Contoh Soal Matriks, Determinan, dan Invers dan Jawaban – Matriks merupakan kumpulan bilangan yang disusun secara baris atau kolom atau kedua-duanya dan di dalam suatu tanda kurung. Sedangkan determinan suatu matriks adalah sebagai selisih antara perkalian elemen-elemen pada diagonal utama dengan perkalian elemen-elemen pada diagonal sekunder. Invers matriks yaitu sebuah kebalikan (invers) dari kedua matriks. Apabila matriks tersebut dikalikan akan menghasilkan matriks persegi (AB = BA = |). Simbol dari invers matriks adalah pangkat -1 dan terletak di atas hurufnya.

Determinan matriks A dapat diperoleh dengan mengurangkan hasil kali elemen-elemen diagonal utama dengan hasil kali elemen-elemen diagonal kedua.
Invers adalah matriks yang elemenya berlawanan atau negarif dari matriks asal, dinotasikan dengan -M. Determinan adalah suatu fungsi yang menghubungkan bilangan real dengan matriks bujur sangkar, dotasi berupa det M.
1 – 10 Soal Matriks Determinan, dan Invers Beserta Jawaban
1. Dari dua buah matriks yang diberikan di bawah ini
Tentukan 2A + B
Jawaban :
Mengalikan matriks dengan sebuah bilangan kemudian dilanjutkan dengan penjumlahan:
2. Diketahui matriks A dan B seperti di bawah ini. Jika determinan matriks A = -8, maka determinan matriks B adalah…
A. 96
B. -96
C. -64
D. 48
E. -48
Jawaban : A
Pembahasan :
Determinan A
det A = (aei + bfg + cdh) – (ceg + afh + bdi) = -8
Determinan B
→ det B = (-12aei + (-12bfg) + (-12cdh)) – (-12ceg + (-12afh) + (-12bdi))
→ det B = -12 {(aei + bfg + cdh) – (ceg + afh + bdi)}
→ det B = -12 det A
→ det B = -12 (-8)
→ det B = 96
3. Nilai z yang memenuhi persamaan di bawah ini adalah…
A. 2
B. -2
C. 4
D. 3
E. -3
Jawaban : B
Pembahasan :
→ 2z2 – (-6) = 8 – (-z(z-1))
→ 2z2 + 6 = 8 – (-z2 + z)
→ 2z2 + 6 = 8 + z2 – z
→ z2 + z – 2 = 0
→ (z + 2)(z – 1) = 0
→ z = -2 atau z = 1
4. Hubungan dua matriks seperti di bawah ini :
Nilai a yang memenuhi persamaan tersebut adalah…
A. 8
B. 24
C. 64
D. 81
E. 92
Jawaban : C
Pembahasan :
28log a – 4a = 4a – (- 2log 6 . 6log 16)
ingat kembali sifat logaritma :
alog b . blog c = alog c
⇒ 2 8log a = 2log 16 = 4
⇒ 8log a = 2
⇒ a = 82
⇒ a = 64
5. Dua buah matriks A dan B masing-masing berturut-turut sebagai berikut:
Jawaban :
Baca Juga : Soal Transformasi Geometri
6. Diketahui :
Tentukan a + b + c!
A. 8
B. 10
C. 12
D. 14
E. 16
Jawaban : D
Pembahasan :
a = 2 ⇒ b = 2a = 4 ⇒ c = ab = 8
a + b + c = 14
7. Tentukan nilai a + b + x + y dari matriks-matriks berikut ini!
Diketahui bahwa P = Q adalah. . .
A. 12
B. 14
C. 16
D. 18
E. 20
Jawaban : C
Pembahasan :
Kesamaan dua buah matriks, terlihat bahwa
3a = 9 → a = 3
2b = 10 → b = 5
2x = 12 → x = 6
y = 6y = 2
Sehingga:
a + b + x + y = 3 + 5 + 6 + 2 = 16
8. Diketahui matriks :
Jika matriks A.B = A+C, maka nilai x+y adalah . . .
A. 2
B. 4
C. 5
D. 6
E. 8
Jawaban : D
Pembahasan :
9. Tentukan determinan dari matriks A berikut ini
A. 10
B. 11
C. 12
D. 13
E. 14
Jawaban : D
Pembahasan :
Menentukan determinan matriks ordo 2 x 2
det A = |A| = ad − bc = (5)(2) − (1)(−3) = 10 + 3 = 13
10. Diberikan sebuah matriks :
Tentukan invers dari matriks P
Jawaban :
Tentukan invers dari matriks P
11 – 20 Soal Matriks Determinan, dan Invers Beserta Pembahasan
11. Tentukan tranpose dari matriks A berikut ini
Jawaban :
Transpose sebuah matriks diperoleh dengan mengubah posisi baris menjadi kolom seperti contoh berikut:
12. Diketahui persamaan matriks
Nilai a + b + c + d =….
A. − 7
B. − 5
C. 1
D. 3
E. 7
Jawaban : D
Pembahasan
Jumlahkan dua matriks pada ruas kiri, sementara kalikan dua matriks pada ruas kanan, terakhir gunakan kesamaan antara dua buah matriks untuk mendapatkan nilai yang diminta.
2 + a = −3
a = − 5
4 + b = 1
b = − 3
d − 1 = 4
d = 5
c − 3 = 3
c = 6
Sehingga
a + b + c + d = −5 − 3 + 6 + 5 = 3
13. Diketahui matriks :
Apabila B − A = Ct = transpos matriks C, maka nilai x .y =….
A. 10
B. 15
C. 20
D. 25
E. 30
Jawaban :
Transpos C diperoleh dengan mengubah posisi baris ke kolom, B − A adalah pengurangan matriks B oleh A
Akhirnya, dari kesamaan dua matriks:
y − 4 = 1
y = 5
x + y − 2 = 7
x + 5 − 2 = 7
x + 3 = 7
x = 4
x . y = (4)(5) = 20
14. Diketahui jika :
maka x + y =….
A. − 15/4
B. − 9/4
C. 9/4
D. 15/4
E. 21/4
Jawaban :
Masih tentang kesamaan dua buah matriks ditambah tentang materi bentuk pangkat, mulai dari persamaan yang lebih mudah dulu:
3x − 2 = 7
3x = 7 + 2
3x = 9
x = 3
4x + 2y = 8
22(x + 2y) = 23
22x + 4y = 23
2x + 4y = 3
2(3) + 4y = 3
4y = 3 − 6
4y = − 3
y = − 3/4
Sehingga:
x + y = 3 + (− 3/4) = 2 1/4 = 9/4
15. Tentukan invers dari matriks :
Jawaban :
Pembahasan :
Baca Juga : Soal Fungsi Komposisi dan Invers
16. Tahukah anda, mengapa suatu bentuk tertentu dikatakan sebagai matriks, apa yang bisa menjelaskan jika bentuk tersebut adalah sebuah matrik?
Jawaban :
Karena, jika bentuk tersebut terdiri dari baris, kolom, maupun keduanya yang membentuk persegi atau persegi panjang dengan ordo nxn
17. Diketahui matriks
Jika matriks A = transpose matriks B, maka nilai a + b + c + d = . . .
Jawaban :
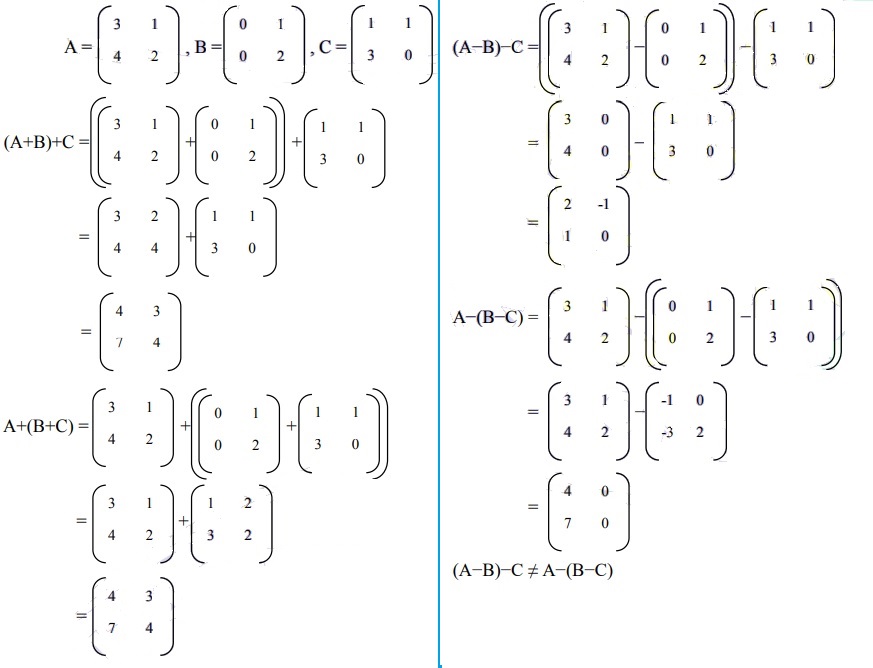
18. Diketahui suatu matriks
Lakukan operasi pada ketiga matriks tersebut, buktikan apa penambahan dan pengurangan matriks tersebut memiliki sifat assosiatif, (A + B)+ C = A + (B +C) dan (A – B) – C = A – (B – C)….?
Jawaban :
19. Diketahui matriks
nilai a dan b yang memenuhi A + 3B = C berturut-turut adalah…
Jawaban :
20. Diketahui jika :
maka ((A+B)(A-B)) –( (A-B)(A+B)) = . . .
Jawaban :
21 – 30 Soal Matriks Determinan, dan Invers Beserta Jawaban
21. Diberikan sistem persamaan
Apabila A menyatakan matriks koefisien sistem persamaan itu, carilah:
a) matriks A,
b) banyak baris dan banyak kolom matriks A masing-masing,
c) elemen-elemen pada baris pertama,
d) elemen-elemen pada kolom kedua,
e) elemen-elemen a13 , a22 ,a23 dan a33 .
Jawaban :
Pembahasan :
22. Diberikan matriks-matriks:
a) tulislah jenis matriks itu,
b) tulislah elemen-elemen diagonal utama,
c) hitunglah banyak elemennya.
Jawaban :
Pembahasan :
23. Diberikan matriks-matriks berikut ini:
Carilah transpos dari setiap matriks itu.
Jawaban :
Pembahasan :
24. Diketahui matriks-matriks:
a) Tentukan A + B dan B + A.
b) Apakah A + B = B + A = O?
c) Apakah A + O = O + A = A?
Jawaban :
Pembahasan :
25. Diketahui matriks-matriks
Jika Xt = Y , maka berturut-turut nilai a dan b.
Jawaban :
Pembahasan :
26. Tentukan masing-masing nilai dari matriks di bawah ini:
Jawaban :
Pembahasan :
27. Diberikan matriks-matriks:
Carilah matriks X berordo 2 yang memenuhi persamaan 2X + Q = 3P.
Jawaban :
Pembahasan :
28. Diketahui :
Carilah nilai x. . .
Jawaban :
Pembahasan :
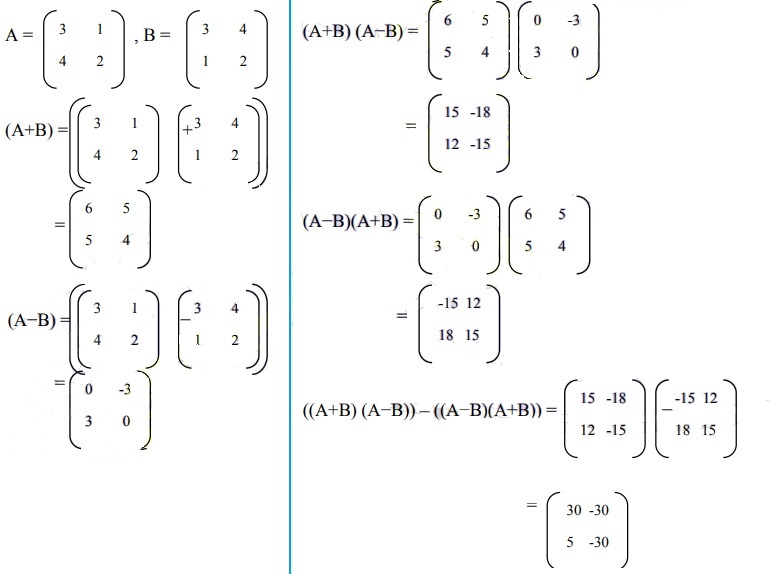
29. Diberikan matriks-matriks
Carilah :
a. (A + B).(A – B)
b. A2 – B2
c. (A + B)2
Jawaban :
Pembahasan :
a. (A + B).(A – B)
Dapat diselesaikan melalui strategi berikut :
b. A2 – B2
Dapat diselesaikan melalui strategi berikut :
c. (A + B)2
Dapat diselesaikan melalui strategi berikut :
30. Tunjukkan bahwa invers dari matriks
adalah matriks A sendiri.
Jawaban :
Pembahasan :
Sudah selesai membaca dan berlatih soal ini ? Ayo lihat dulu Soal Matematika lainnya

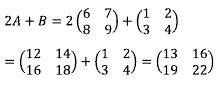
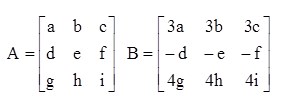
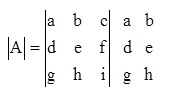
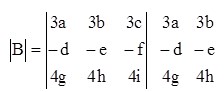
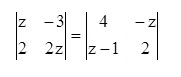
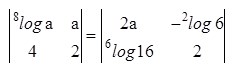
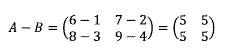
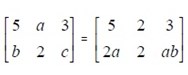
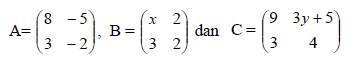
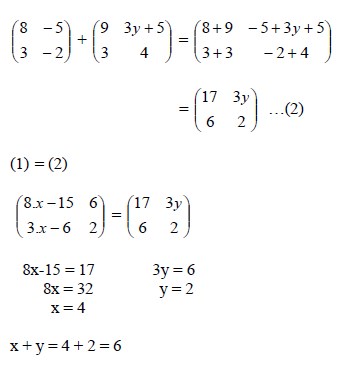
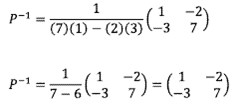
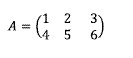
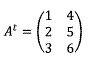
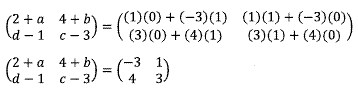
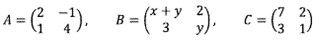
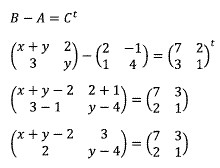
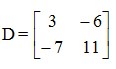
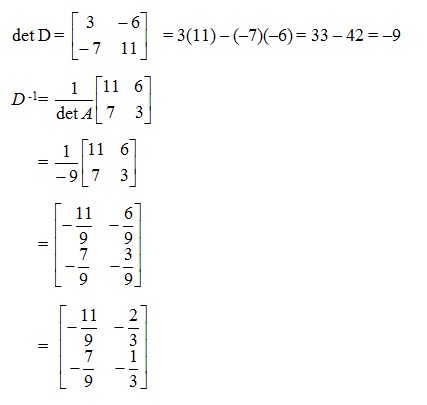
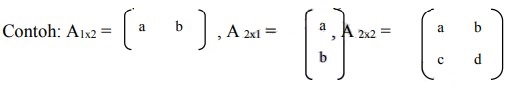
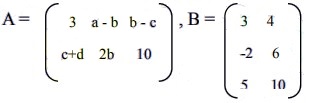
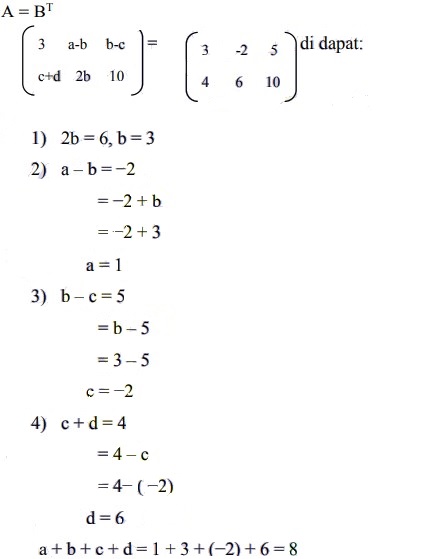
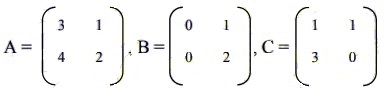
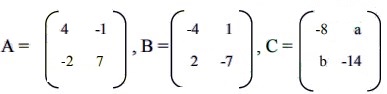
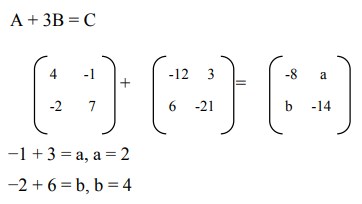
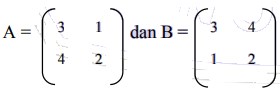
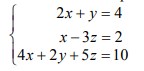

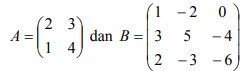


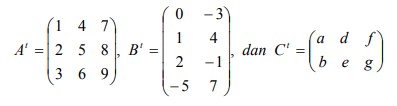
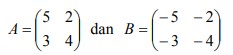

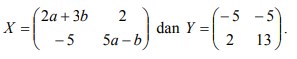
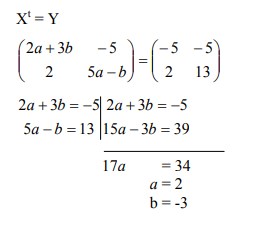
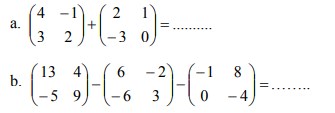
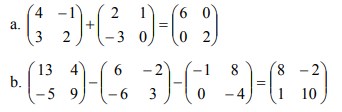
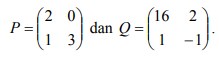
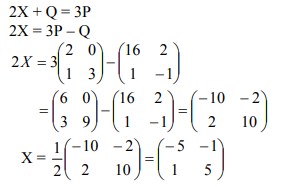
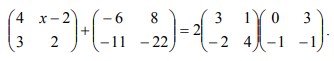
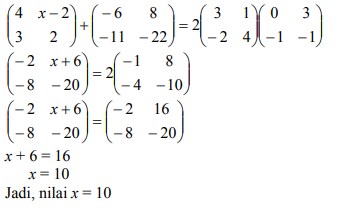
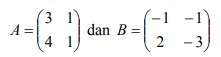
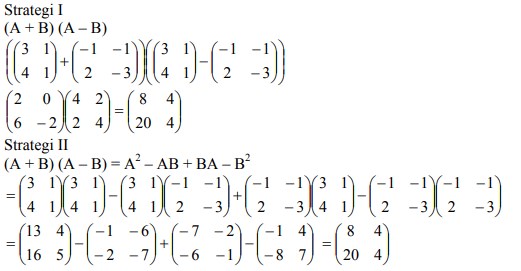
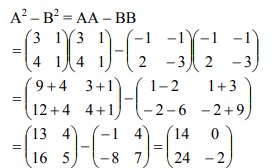
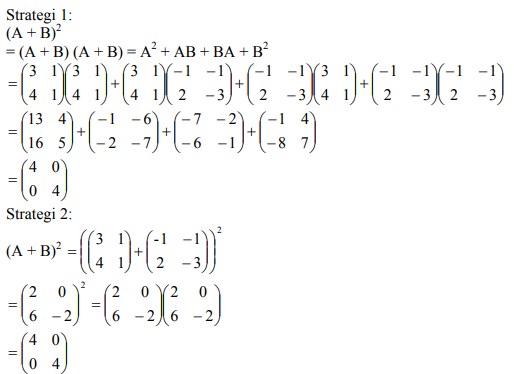
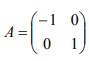




Saya gak tau.gak ada guru ajarin karna gak sekolah jadi gak paham penyebabnya adalah corona jadi saya gak sekolah.jika anda bertanya kenapa saya gak bertanya sama guru saya ialah saya tinggal jauh dari rumah yaitu saya pesantren jadi gak bisa bertanya gak ngerti juga meski sudah diterangkan.saya hanya mengerti bila dijelaskan langsung dari sekolah.jadi saya gak ngerti soalnya😭😭😭😭😭
Mantap banget kak
Web yang high rekomen buat persiapan ujian makasi bngt
Keren.Selalu pake web ini buat latihan kalo mau ulangan harian.Soalnya berbobot dan menyeluruh.Terimakasih dan sukses selalu.
downloadnya ada ngg kak?