Contoh Soal Bentuk Pangkat, Akar dan Logaritma dan Jawaban – Jika akar adalah bentuk lain dari pangkat, maka logaritma adalah lawan dari pangkat. Jika dalam pangkat yang kita cari adalah hasil dari perkalian berulang tersebut maka logaritma adalah mencari berapa banyak perkalian yang terjadi alias mencari pangkat itu sendiri.

Logaritma merupakan operasi matematik yaitu kebalikan (atau invers) dari eksponen atau pemangkatan. Di dalam matematika, akar kuadrat dari bilangan x sama dengan bilangan r sedemikian sehingga r² = x, atau, di dalam perkataan lain, bilangan r yang bila dikuadratkan (hasil kali dengan bilangan itu sendiri) sama dengan x.
Bentuk akar merupakan bilangan-bilangan dibawah akar yang hasilnya merupakan bilangan irasional.

Logaritma adalah kebalikan dari perpangkatan. Jadi apabila diketahui
ax =b maka x dapat ditentukan dengan logaritma yang berbentuk x = a log b
a : bilangan pokok logaritma dengan a > 0, a = 1
b : Numerus , b > 0

1 – 10 Soal Bentuk Pangkat, Akar dan Logaritma dan Jawaban
1. Sederhanakan bentuk akar dan pangkar berikut ini :
A. 26x-13
B. 23x-13
C. 22x-13
D. 26x-12
E. 23x-12
Jawaban : A
Pembahasan :
2. Tentukan nilai p yang memenuhi persamaan berikut:
A. 1
B. 2
C. 3
D. 4
E. 5
Jawaban : C
Pembahasan
3. Jika a = 4, b = 3, dan c = 2, tentukan nilai dari:
A. 3
B. 9
C. 18
D. 27
E. 36
Jawaban : D
Pembahasan
4. Tentukan nilai dari: 2log 8 + 3log 9 + 5log 125 adalah…
A. -4
B. -8
C. 0
D. 4
E. 8
Jawaban : E
Pembahasan :
2log 8 + 3log 9 + 5log 125
= 2log 23 + 3log 32 + 5log 53 = 3 2log 2 + 2 3log 3 + 3 5log 5
= 3 + 2 + 3 = 8
5. Tentukan nilai dari 2log 1/8 + 3log 1/9 + 5log 1/125 adalah…
A. -4
B. -8
C. 0
D. 4
E. 8
Jawaban : B
Pembahasan :
2log 1/8 + 3log 1/9 + 5log 1/125
= 2log 2−3 + 3log 3−2 + 5log 5−3
= − 3 − 2 − 3 = − 8
Baca Juga : Soal Induksi Matematika
6. Tentukan nilai dari 4log 8 + 27log 9 adalah. . .
A. 10/6
B. 12/6
C. 13/6
D. 14/6
E. 15/6
Jawaban : C
Pembahasan :
4log 8 + 27log 9
= 22log 23 + 33log 32
= 3/2 2log 2 + 2/3 3log 3
= 3/2 + 2/3 = 9/6 + 4/6 = 13/6
7. Tentukan nilai dari 8log 4 + 27log 1/9 adalah. . .
A. -2
B. -1
C. 0
D. 1
E. 2
Jawaban : C
Pembahasan :
8log 4 + 27log 1/9
23log 22 + 33log 3−2
= 2/3 2log 2 + (−2/3) 3log 3
= 2/3 − 2/3 = 0
8. Bentuk sederhana dari :
maka hasilnya adalah. . .
A. (3ab)2
B. 3(ab)2
C. 9 (ab)2
D. 3/(ab)2
E. 9/(ab)2
Jawaban : E
Pembahasan :
Kalikan semua pangkat dengan − 1 seperti permintaan soal, kemudian sederhanakan pangkat dari koefisien yang pada sama.
9. Bentuk sederhana dari :
maka hasilnya adalah. . .
A. 61/4
B. 63/4
C. 63/2
D. (2/3)3/4
E. (3/2)3/4
Jawaban : B
Pembahasan :
Sifat yang digunakan adalah
axay = ax + y dan
ax : ay = ax − y
10. Jika a = 2, x = 10, y = 5, dan z = 12 tentukan nilai dari :
maka hasilnya adalah. . .
A. 2
B. 4
C. 8
D. 12
E. 16
Jawaban : C
Pembahasan :
Perkalian dan pembagian bentuk pangkat
11 – 20 Soal Bentuk Pangkat, Akar dan Logaritma dan Jawaban
11. Tentukan nilai dari √2log 8 adalah. . .
A. 10
B. 8
C. 6
D. 4
E. 2
Jawaban : C
Pembahasan :
√2log 8
= 21/2log 23 = 3/0,5 2log 2 = 3/0,5 = 6
12. Tentukan nilai dari √3log 27 adalah. . .
A. 10
B. 8
C. 6
D. 4
E. 2
Jawaban : D
Pembahasan :
√3log 9
= 31/2log 32 = 2/0,5 3log 3 = 2/0,5 = 4
13. Diketahui:
log p = A
log q = B
Tentukan nilai dari log p3 q2 adalah . . .
A. 2A + 2B
B. 2A + 3B
C. 3A + 3B
D. A + B
E. 3A + 2B
Jawaban : E
Pembahasan :
log p3 q2 = log p3 + log q2 = 3 log p + 2 log q = 3A + 2B
14. Diketahui log 40 = A dan log 2 = B, tentukan nilai dari log 20 adalah. . .
A. 2A − B
B. 2A + B
C. A − 2B
D. A + B
E. A − B
Jawaban : E
Pembahasan
log 20 = log 40/2 = log 40 − log 2 = A − B
15. Diketahui 2log √ (12 x + 4) = 3. Tentukan nilai x
A. 1
B. 2
C. 3
D. 4
E. 5
Jawaban : E
Pembahasan
2log √ (12 x + 4) = 3
Ruas kiri bentuknya log, ruas kanan belum bentuk log, ubah dulu ruas kanan agar jadi bentuk log. Ingat 3 itu sama juga dengan 2log 23 . Ingat rumus alog ab = b jadi
2log √( 12 x + 4) = 2log 23
Kiri kanan sudah bentuk log dengan basis yang sama-sama dua, hingga tinggal menyamakan yang di dalam log kiri-kanan atau coret aja lognya:
2log √( 12 x + 4) = 2log 23
√( 12 x + 4) = 23
√( 12 x + 4) = 8
Agar hilang akarnya, kuadratkan kiri, kuadratkan kanan. Yang kiri jadi hilang akarnya:
12 x + 4 = 82
12x + 4 = 64
12 x = 60
x = 60/12 = 5
Baca Juga : Soal Matriks, Determinan dan Invers
16. Ditentukan nilai a = 9, b = 16 dan c = 36. Nilai dari
maka hasilnya adalah. . .
A. 3
B. 6
C. 9
D. 12
E. 18
Jawaban : C
Pembahasan
17. Bentuk sederhana dari (1 + 3√2) − (4 − √50) adalah…
A. −2√2 − 3
B. −2√2 + 5
C. 8√2 − 3
D. 8√2 + 3
E. 8√2 + 5
Jawaban : C
Pembahasan
Hilangkan tanda kurungnya dulu, jika ada tanda minus di depan kurung, kalikan masuk, jadinya
(1 + 3√2) − (4 − √50)
= 1 + 3√2 − 4 + √50
√50 sama saja dengan √25 × √ 2 jadi sama dengan 5√2, tinggal disederhanakan:
= 1 + 3√2 −4 + 5√2
= 1 − 4 + 3√2 + 5√2
= −3 + 8√2
= 8√2 −3
18. Ubah bentuk akar berikut ke bentuk pangkat!
A. x1/6
B. x3/4
C. x3/2
D. x3/6
E. x3/8
Jawaban : C
Pembahasan
19. Bentuk sederhana dari (3√3 – 2√2)(2√3 – √2)=…..
A. 22 + √6
B. 14 + √6
C. 22 – √6
D. 22 – 7√6
E. 14 – 7√6
Jawaban : D
Pembahasan
Menyederhanakan bentuk akar, kalikan saja:
(3√3 – 2√2)(2√3 – √2)
= 18 – 3√6 – 4√6 + 4
= 22 – 7√6
20. Bentuk sederhana dari
maka hasilnya adalah. . .
A. – 4 – 3√6
B. – 4 – √6
C. – 4 + √6
D. 4 – √6
E. 4 + √6
Jawaban : E
Pembahasan
Sudah selesai membaca dan berlatih soal bentuk pangkat, akar dan logaritma ini ? Ayo lihat dulu Soal Matematika lainnya

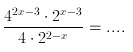
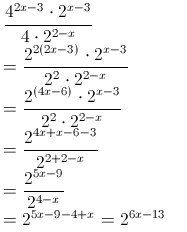
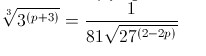

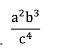
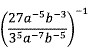
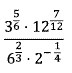
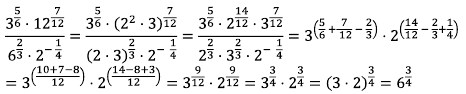
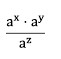
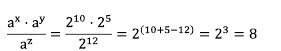
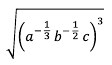
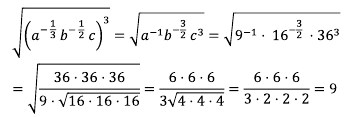
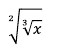
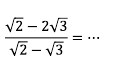




Trmksh sdh di bantu
Izin minta jawaban Dan soal