Contoh Soal Ujian Matematika Kelas 11 Semester 1 dan Kunci Jawaban Kurikulum 2013 – Berikut ini adalah 20 butir contoh soal matematika semester 1 untuk siswa pelajari dalam menghadapi ujian sekolah K13.
Pada kelas 2 semester ganjil siswa mempelajari materi :
- Logika Matematika
- Induksi Matematika
- Pertidaksamaan Linear Dua Variabel
- Program Linear
- Matriks Dasar & Operasi Matriks

1 – 10 Contoh Soal Ujian Matematika dan Jawaban Beserta Pembahasan
1. Jika diketahui P(x) = 2x3+4x2-3x+2, maka nilai dari P(5) adalah …
A. 57
B. 75
C. 337
D. 373
E. 377
Jawaban : C
Pembahasan :
(5) = 2.125 + 4.25 − 3.5 + 2 (5) = 337
2. Jika P(x) = 3x4-(m-1)x3+2(n-1)x+6 dan Q (x) = ax4-bx2+6x+c maka nilai dari m+n adalah …
A. 3
B. 4
C. 5
D. 6
E. 7
Jawaban : C
Pembahasan :
Soal tersebut adalah tentang kesamaan fungsi, sehingga kita menyamakan koefisien dari suku yang mempunyai derajat pangkat sama.
−(𝑚𝑚 − 1) = 0
𝑚𝑚 = 1
2(𝑛𝑛 − 1) = 6
2𝑛𝑛 − 2 = 6 → 𝑛𝑛 = 4
𝑛𝑛 + 𝑚𝑚 = 1 + 5 = 5
3. Jika 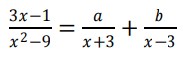
A. 3
B. 2/3
C. -2
D. 1/3
E. ¾
Jawaban : D
Pembahasan :
4. Jika 𝑥6 − 3𝑥4 − 𝑥2 + 2𝑥 + 4 = (𝑥 + 1)𝑄(𝑥) + 𝑘 maka nilai k …
A. -3
B. -2
C. -1
D. 3
E. 4
Jawaban : C
Pembahasan :
Suatu fungsi dapat dinyatakan dengan hasil kali antara pembagi dan hasil bagi kemudian dijumlahkan dengan sisanya. Dalam soal tersebut (𝑥 + 1) merupakan pembagi, Q(x) merupakan
hasil bagi dan k adalah sisanya. Teorema sisa menyatakan bahwa sisa merupakan fungsi dari nilai pembagi fungsi tersebut. Pembagi adalah (𝑥 + 1), maka 𝑥 = −1. Selanjutnya kita masukkan nilai tersebut ke dalam fungsi.
F(x) = 𝑥6 − 3𝑥4 − 𝑥2 + 2𝑥 + 4
𝐹(−1) = 1 − 3 − 1 − 2 + 4
𝐹(−1) = −1
Berdasarkan teorema sisa maka -1 merupakan sisa dari fungsi tersebut. Maka nilai k= – 1
5. Jika 𝑃(𝑥) = 3𝑥3 − 2𝑥 + 4 dibagi (𝑥 − 1), maka sisanya …
A. 5
B. 6
C. 7
D. 8
E. 10
Jawaban : A
Pembahasan :
Pembagi adalah (𝑥 − 1) maka x = 1
𝑃(1) = 3 − 2 + 4
𝑃(1) = 5
Maka sisa dari hasil pembagian tersebut adalah 5
Simak Juga : Soal Ujian Matematika Kelas 10 SMA Semester 1 K.13
6. Jika P(x) dibagi 𝑥² + 𝑥 sisanya 3𝑥 + 8, jika P(x) dibagi (𝑥 + 1) sisanya …
A. -11
B. -8
C. 2
D. 3
E. 5
Jawaban : E
Pembahasan :
Jika suku banyak dibagi oleh fungsi yang berderajat 2 maka sisanya dalam bentuk (𝑎𝑥 + 𝑏). Pembagi berderajat 2 dalam soal tersebut adalah 𝑥² + 𝑥 dan sisanya adalah 3𝑥 + 8.
𝑥² + 𝑥 = 𝑥(𝑥 + 1)
Untuk pembagi berderajat satu, maka sisanya adalah konstanta. Pembagi berderajat 1 adalah (𝑥𝑥 + 1) yang juga merupakan salah satu faktor dari pembagi berderajat 2, maka
𝑆(𝑥) = 𝑎𝑥 + 𝑏
𝑆(−1) = 3(−1) + 8
𝑆(−1) = 5
7. Suku banyak 2𝑥5 − 3𝑥4 − 𝑥2 + 2𝑥 − 1 dibagi 𝑥3 − 1, maka sisanya adalah …
a. 𝑥2 − 𝑥 − 1
b. 𝑥2 − 𝑥
c. −3𝑥2 − 𝑥 + 1
d. 𝑥2 + 𝑥 − 1
e. 𝑥2 + 2𝑥 − 1
Jawaban : A
Pembahasan :
Dengan cara pembagian biasa kita dapatkan hasil 2𝑥2 − 3𝑥 dan sisanya 𝑥2 − 𝑥 − 1
8. Jika (2𝑥 − 1) adalah faktor dari suku banyak 𝑃(𝑥) = 2𝑥³ + 7𝑥² + 𝑎𝑥 − 3 maka faktor lainnya adalah …
A. (𝑥 − 3) dan (𝑥 + 1)
B. (𝑥 + 3) dan (𝑥 + 1)
C. (𝑥 + 3) dan (𝑥 − 1)
D. (𝑥 − 3) dan (𝑥 − 1)
E. (𝑥 + 2) dan (𝑥 − 6)
Jawaban : B
Pembahasan :
Teorema faktor menyatakan bahwa jika suatu fungsi dibagi menggunakan akarnya maka sisanya adalah 0.
Maka fungsi P(x) menjadi
𝑃(𝑥) = 2𝑥³ + 7𝑥² + 𝑎𝑥 − 3
Dengan menggunakan cara horner, jika P(x) dibagi (2𝑥 − 1) maka sisanya adalah:
𝑆(𝑥) = 2𝑥² + 8𝑥 + 6
Untuk mencari 2 faktor yang lain, maka persamaan tersebut kita faktorkan
0 = 2𝑥² + 8𝑥 + 6
0 = 𝑥² + 4𝑥 + 3
0 = (𝑥 + 3)(𝑥 + 1)
9. Jika P(x) dibagi (𝑥 − 2) sisanya -3 dan jika dibagi (𝑥 + 1) sisanya 6. Jika P(x) dibagi 𝑥² − 𝑥 − 2 adalah …
A. – 𝑥 + 5
B. −3𝑥 + 3
C. 𝑥 − 1
D. −9𝑥 + 5
E. 𝑥 + 3
Jawaban : B
Pembahasan :
Jika 𝑥² − 𝑥 − 2 kita faktorkan hasilnya adalah (𝑥 − 2) dan (𝑥 + 1). Jika pembaginya berderajat 2, maka sisanya dalam bentuk 𝑎𝑥 + 𝑏. Dengan menggunakan teorema sisa dapat kita peroleh bahwa sisa merupakan fungsi dari pembagi :
𝑆(𝑥) = 𝑎𝑥 + 𝑏
𝑆(2) = 2𝑎 + 𝑏
−3 = 2𝑎 + 𝑏 (1)
𝑆(−1) = −𝑎 + 𝑏
6 = −𝑎 + 𝑏 (2)
Dengan mengeliminasi kedua persamaan tersebut, didapatkah a = -3 dan b = 3 sehingga sisanya adalah 𝑆(𝑥) = −3𝑥 + 3
10. Diketahui persamaan suku banyak 𝑥³ − 9𝑥 + 𝑚 = 0, nilai m jika 2 akarnya berlawanan adalah …
A. -2
B. -1
C. 0
D. 2
E. 4
Jawaban : C
Pembahasan :
Persamaan tersebut mempunyai 2 akar berlawanan, kita misalkan:
𝑥1 = 𝑝
𝑥2 = −𝑝 (berlawanan dengan 𝑥1)
𝑥3 = 𝑞
Selanjutnya akar-akar tersebut kita masukkan ke sifat-sifat persamaan berderajat 3, yaitu:
Semua bilangan jika dikalikan 0 hasilnya juga 0, maka nilai m adalah 0.
11 – 20 Contoh Soal Ujian Matematika Kelas 11 dan Jawaban
11. Jika 𝑓(𝑥) = 2𝑥² + 5𝑥 dan 𝑔(𝑥) = 1/𝑥 maka (f o g)(2) adalah …
A. 3
B. 2
C. 1
D. ½
E. 1/3
Jawaban : A
Pembahasan :
Pertama kita cari fungsi (f o g)
12. Diketahui domain fungsi (𝑓 + 𝑔𝑥) adalah …
A. {𝑥|𝑥 ≥ 3, 𝑥 ∈ 𝑅}
B. {𝑥|𝑥 ≤ 5, 𝑥 ∈ 𝑅}
C. {𝑥|3 ≤ 𝑥 ≤ 5, 𝑥 ∈ 𝑅}
D. {𝑥|3 < 𝑥 < 5, 𝑥 ∈ 𝑅}
E. {𝑥|3 ≤ 𝑥 < 5, 𝑥 ∈ 𝑅}
Jawaban : C
Pembahasan :
Domain fungsi dalam bentuk akar kuadrat adalah yang didalam akar harus lebih besar atau sama dengan 0, maka
2𝑥 − 6 ≥ 0
𝑥 ≥ 3
dan
5 − 𝑥 ≥ 0
𝑥 ≤ 5
Karena fungsinya adalah (𝑓 + 𝑔)(𝑥) maka domainnya harus memenuhi kedua batas tersebut
{𝑥|3 ≤ 𝑥 ≤ 5, 𝑥 ∈ 𝑅}
13. . Diketahui fungsi 𝑓(𝑥) = 2𝑥 + 1 dan 𝑔(𝑥) = 𝑥² − 3𝑥 + 3. Jika nilai (gof)(𝑡) = 7 maka nilai t adalah …
A. 1 atau 2
B. -2/3 atau 1
C. -1 atau 2/3
D. -1 atau 3/2
E. -2 atau -1
Jawaban : D
Pembahasan :
14. Jika 𝑓(2𝑥 − 3) = 5𝑥 + 1 maka 𝑓‾¹(−4) adalah …
A. -19
B. -11
C. -5
D. -3
E. 1
Jawaban : C
Pembahasan :
15. Invers dari fungsi 𝑓(𝑥) = 5𝑥−1− 3 adalah …
a. log5 (5𝑥 + 15)
b. log5 (𝑥 + 4)
c. log5 (𝑥 + 3)
d. -1 + log5 (𝑥 + 3)
e. 1 − log5 (𝑥 + 3)
Jawaban : A
Pembahasan :
Lihat Juga : Contoh Soal Faktorial Pilihan Ganda dan Jawaban
16. Diketahui 𝑓(𝑥) = 1/𝑥 dan 𝑔(𝑥) = 2𝑥 −1 maka nilai (𝑔‾¹𝑜𝑓‾¹)(𝑥) adalah …
Jawaban : B
Pembahasan :
Ada 2 cara untuk menyelesaikan soal tersebut, yaitu dengan menginvers masing-masing fungsi kemudian di komposisikan, atau menggunakan :
17. Perhatikan :
Wawan rajin belajar maka naik kelas
Wawan dapat hadiah atau tidak naik kelas
Wawan rajin belajar
Kesimpulan yang sah adalah…
a. Wawan dapat Hadiah
b. Wawan tidak dapat hadiah
c. Wawan naik kelas dan dapat hadiah
d. Wawan dapat hadiah atau naik kelas
Jawaban : A
Pembahasan :
Misalkan
𝑝: Wawan rajin belajar.
𝑞: Wawan naik kelas.
𝑟: Wawan dapat hadiah.
Jadi diperoleh
P1: 𝑝 ⟹ 𝑞
P2: 𝑟 ∨ ~𝑞 ≅ (~𝑟 ⟹ ~𝑞) ≅ 𝑞 ⟹ 𝑟
P3: 𝑝
Perhatikan bahwa 𝑝 ⟹ 𝑞 dan dilain pihak, 𝑟 ∨ ~𝑞 ≅ (~𝑟 ⟹ ~𝑞) ≅ 𝑞 ⟹ 𝑟
Jadi diperoleh 𝑝 ⟹ 𝑞 dan 𝑞 ⟹ 𝑟, dengan demikian berdasarkan silogisme haruslah
𝑝 ⟹ 𝑟 jadi kesimpulan jawabannya adalah wawan dapat hadiah.
18. Diketahui premis-premis sebagai berikut :
- Premis I : “Jika Anto lulus ujian maka saya diajak kebandung.”
- Premis II :” Saya tidak diajak kebandung.”
Kesimpulan yang sah dari premis-premis tersebut adalah…..
a. Jika saya tidak pergi ke Lembang maka Anto lulus ujian.
b. Jika Anto Lulus Ujian maka saya pergi ke Lembang.
c. Anto lulus ujian dan saya pergi ke Lembang.
d. Anto tidak lulus ujian.
Jawaban : D
Pembahasan :
𝑝: Anto lulus ujian.
𝑞: Saya diajak kebandung.
Jadi diperoleh
P1: 𝑝 ⟹ 𝑞
P2: ~𝑞
Dengan demikian, berdasarkan Modus Tollens, kesimpulannya haruslah ~𝑝 yaitu Anto tidak lulus ujian
19. Ingkaran dari pernyataan “Semua anak-anak suka permen.” Adalah …
a. Tidak ada anak-anak yang suka permen.
b. Semua anak-anak tidak suka permen.
c. Ada anak-anak yang tidak suka permen.
d. Tidak ada anak-anak yang tidak suka permen.
Jawaban : C
20. Negasi dari pernyataan “Hari ini tidak hujan dan saya tidak membawa payung” adalah
a. Hari ini hujan tetapi saya tidak membawa payung
b. Hari ini tidak hujan tetapi saya membawa payung
c. Hari ini tidak hujan atau saya tidak membawa payung
d. Hari ini hujan atau saya membawa payung
Jawaban : D
Sudah selesai membaca dan berlatih soal ini ? Ayo lihat dulu Soal Matematika lainnya


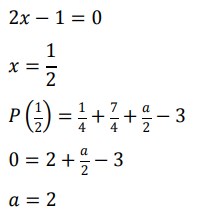
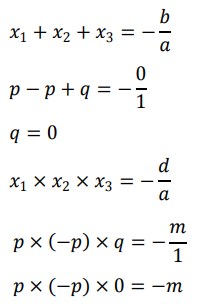
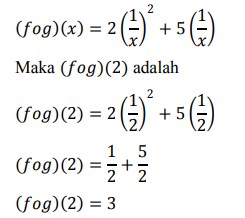


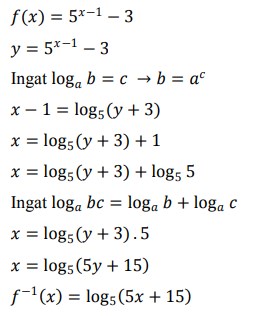
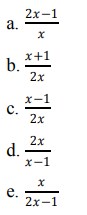




Suda mi pak tugas ku
Soalya sangat muda